THUSSAT7月测试理科数学试卷 8页

中学生标准学术能力诊断性测试 2019 年 7 月测试 数学试卷 本试卷共 150 分，考试时间 120 分钟。 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．已知全集    2, 1,0,1,2 , , ,U A y y x x U= − − = =  则 UCA= A． B． C． D． 2．已知 i 为虚数单位， 3 iz i += ，则 z 的虚部为 A． B． C． D． 3．已知函数 ()fx是定义在 R 上的奇函数，且 ( 4) ( )f x f x+ = − ，当 ( )0 ,2x  时， 3( ) 2f x x=+ ， 则 ( 7 )f = A． B． C． D． 4．设  sin22sin3 = ， )0,2(  − ，则 的值是 A． B． C． D． 5．已知数列  na 的通项为 kn nan − += 2 ，对任意 *nN ，都有 6aan  ，则正数 k 的取值范围是 A． B． C． D． 76  k 6．已知函数 ()fx在区间( , )ab上可导，则“函数 ()fx在区间( , )ab上有最大值”是“存在 0 ( , )x a b 满足 0( ) 0fx = 的” A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件  0,1 , 2  2 , 1,0−−  1, 2−−  1,2 1 3− i 3i− 3 3− 2 2− t a n 2  7 24 7 24− 7 32 7 32− 6k 65  k 6k 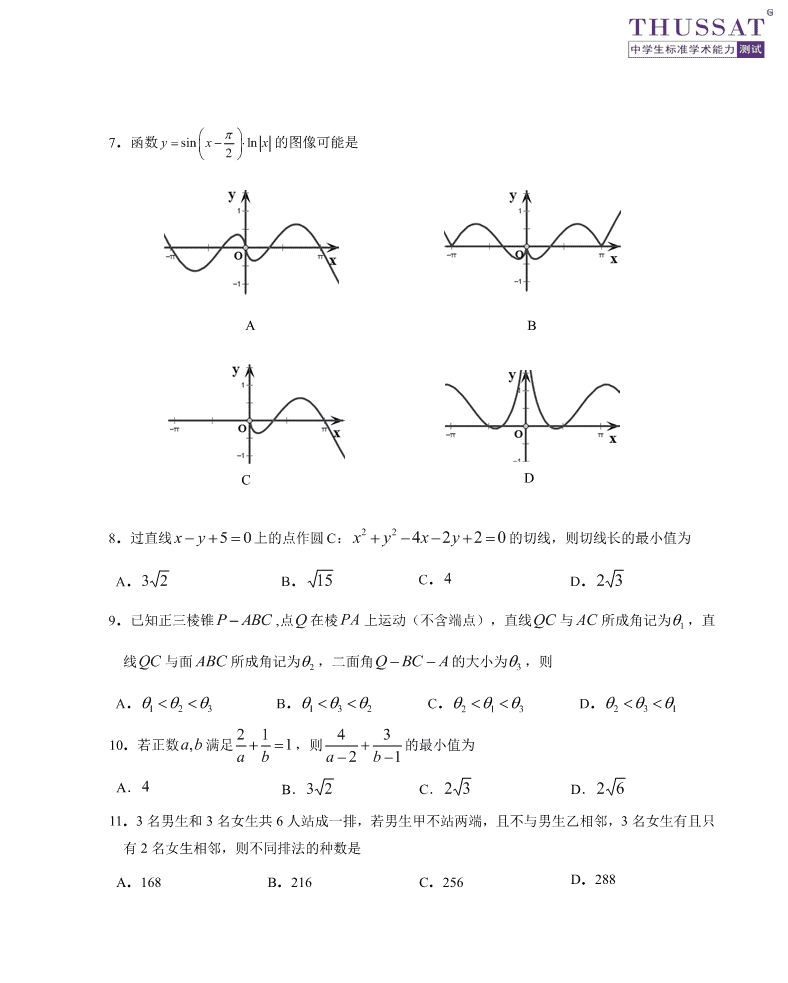7．函数 sin l n 2y x x = −   的图像可能是 8．过直线 05 =+− yx 上的点作圆 C： 022422 =+−−+ yxyx 的切线，则切线长的最小值为 A． 23 B． 15 C． 4 D． 32 9．已知正三棱锥 ABCP − ,点 Q 在棱 PA 上运动（不含端点），直线 QC 与 AC 所成角记为 1 ，直 线 QC 与面 ABC 所成角记为 2 ，二面角 ABCQ −− 的大小为 3 ，则 A． 321   B． 231   C． 312   D． 132   10．若正数 ,ab满足 211ab+=，则 43 21ab+−− 的最小值为 A． 4 B． 23 C． 32 D． 62 11．3 名男生和 3 名女生共 6 人站成一排，若男生甲不站两端，且不与男生乙相邻，3 名女生有且只 有 2 名女生相邻，则不同排法的种数是 A．168 B．216 C．256 D．288 A B C D 12．若平面向量 a,b,e 满足 2 3 1a , b , e= = = ，且 ( ) 10a b e a b −  + + = ，则 ab− 的最小值为 A． 1 B． 2 3 1− C． 3 2 1 − D ． 6 二．填空题：本大题共 4 小题，每小题 6 分，共 24 分． 13．某几何体的三视图如下图所示，则该几何体的体积为 14．已知数列  na 的通项公式为 ( ) ( )231 −−= na n n ，则数列  na 的前 n 项和 nS = 15．已知 F 为双曲线 12 2 2 2 =− b y a x 的左焦点，过点 F 的直线与圆： 2 2 22 cyx =+ 交于 ,AB两点 （ A 在 ,FB之间），与双曲线在第一象限的交点为T , O 为坐标原点．若 BTFA = ， 90AOB =，则双曲线的离心率为 16． 若 a 为实数，且关于 x 的方程 2221x a x x− + − = 有实数解，则 a 的取值范围是 （第 13 题图） 三、解答题：共 66 分．解答应写出文字说明、证明过程或推演步骤． 17 ． （本题满分 12 分）已知 cba ,, 分别是 ABC 的 三 个 内 角 CBA ,, 的对边，且满足 Baba 2222 cos434 =− ． （1）求角 A 的大小； （2）当 A 为锐角时，求函数 )6sin(sin3 ++= CBy 的最大值． 18．（本题满分12 分）如图，已知多面体 1111AB CD A B C D− ， 1111, , ,A A B B CC D D 均 垂 直 于 平 面 ABCD ， AD BC∥ ， 11=2AB BC CD AA CC= = = = ， 1 =1BB ， 1 4AD DD==． （1）证明： 11AC ⊥ 平面 11CDD C ． （2）求直线 1BC 与平面 1 1 1A B C 所成角的正弦值． 19．（本题满分 12 分）甲、乙、丙、丁四位同学报名参加校运会“跳高”、“跑步”、“铅球”三个项 目的比赛，若每位同学只能报其中一个项目，且报名其中任一个项目都是等可能的． （1）求这四位同学中有且仅有两位同学报同一个项目的概率； （2）求这四位同学报名参加校运会项目的个数  的分布列与期望． 20．（本题满分 15 分）已知抛物线 2 2 1: xyC = 与直线 1: −= kxyl （ k 为常数）无交点，设点 P 为 直线 l 上的动点，过 P 作抛物线 C 的两条切线， BA, 为切点. （1）证明：直线 AB 恒过定点 Q ； （2）试求 PAB 面积的最小值． y 21．（本题满分 15 分）已知函数 1( ) ( 1)ln( 2) 2xf x e a x x x+= − + + − − , 1x − ， aR . （1）当 1 2a = 时，求证： ( ) 0fx 恒成立； （2）若 ( ) 0fx 恒成立，求实数 a 的取值范围．