角的比较与补(余)角（第一课时）教案 3页

‎ ‎ ‎4．5　角的比较与补(余)角 第一课时 教学目标　　　　　‎ 知识与技能：‎ ‎1．会比较角的大小，能估计一个角的大小．在操作活动中认识角的平分线．‎ ‎2．理解两角互余、互补的概念及其性质．‎ 过程与方法：‎ 通过实际观察、操作，体会角的大小，并简单说理，培养学生的观察思维能力及合情推理能力．‎ 情感、态度与价值观：‎ 通过角的测量和折叠等，体验数、符号和图形是描述现实世界的重要手段．‎ 学情介绍　　　　　‎ 学生对角的认识是从形到数的刻画，学生对角平分线以及补角、余角的理解是很容易的，但运用几何语言表达对学生来说比较困难．‎ 内容分析　　　　　‎ 本节课对角的认识是从定性到定量，是前面所学角知识的延续，也是为后面学习三角形、四边形等知识作铺垫．‎ 教学重、难点　　　‎ 重点：角的大小比较方法以及角的平分线的概念，两角互补、互余的概念及性质．‎ 难点：从图形中观察角的数量关系．‎ 一、新课引入 导语：如图，已知∠α和∠β，如何比较这两个角的大小呢？‎ 今天我们就来学习角的大小比较．‎ 二、讲授新课 ‎【问题展示】‎ 如图，已知∠ABC和∠DEF. ‎ 请大家讨论一下，用什么方法可以比较这两个角的大小？‎ ‎【合作探究】‎ 分组讨论角的比较方法．在学生讨论过程中，教师深入学生中间巡视，观察并听取他们解决问题的方法和建议．‎ 3‎ ‎ ‎ ‎【问题解答】‎ 比较方法：‎ ‎(1)度量方法：用量角器量出角的度数，然后比较它们的大小．‎ ‎(2)叠合方法：把两个角叠合在一起比较大小．‎ ‎【问题展示】‎ 在一副三角尺中，每块都有一个角是90°，而其他两个角的和是90°.一般情况下，如果两个角的和等于一个直角，我们就称这两个角互为余角，即其中一个角是另一个角的余角．例如，∠1与∠2互为余角，∠1是∠2的余角，∠2也是∠1的余角．‎ 同样，如果两个角的和等于180°(平角)，就说这两个角互为补角，即其中一个角是另一个角的补角．‎ 如果∠1与∠2互余，∠3与∠4互余，并且∠1=∠3，那么∠2与∠4相等吗？为什么？‎ 如果∠1与∠2互补，∠3与∠4互补，并且∠1=∠3，那么∠2与∠4相等吗？为什么？‎ ‎【合作探究】‎ 生：学生分组讨论、交流．‎ ‎【问题解答】‎ 同角(或等角)的补角相等；同角(或等角)的余角相等．‎ ‎【问题展示】‎ 做一做：在一张透明纸上任意画一个角∠AOB，把这张透明纸折叠，使角的两边OA与OB重合，然后把这张纸展开、铺平，画出折痕OC.试比较∠AOC与∠BOC的大小．‎ ‎【合作探究】‎ 生：学生动手操作．‎ ‎【问题解答】‎ 从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线．射线OC就是∠AOB的平分线，这时∠AOC=∠BOC=∠AOB.‎ 三、巩固新知 ‎【小组讨论】‎ 如图，∠ABC=90°，∠CBD=30°，BP平分∠ABC.求∠DBP的度数．‎ ‎【点拨】 解：∵∠ABC=90°，BP平分∠ABC，‎ ‎∴∠PBC=∠ABC=×90°=45°.‎ ‎∴∠DBP=∠PBC-∠CBD=45°－30°=15°.‎ 四、小结与评价 本节课主要学习了哪些知识？你有哪些收获？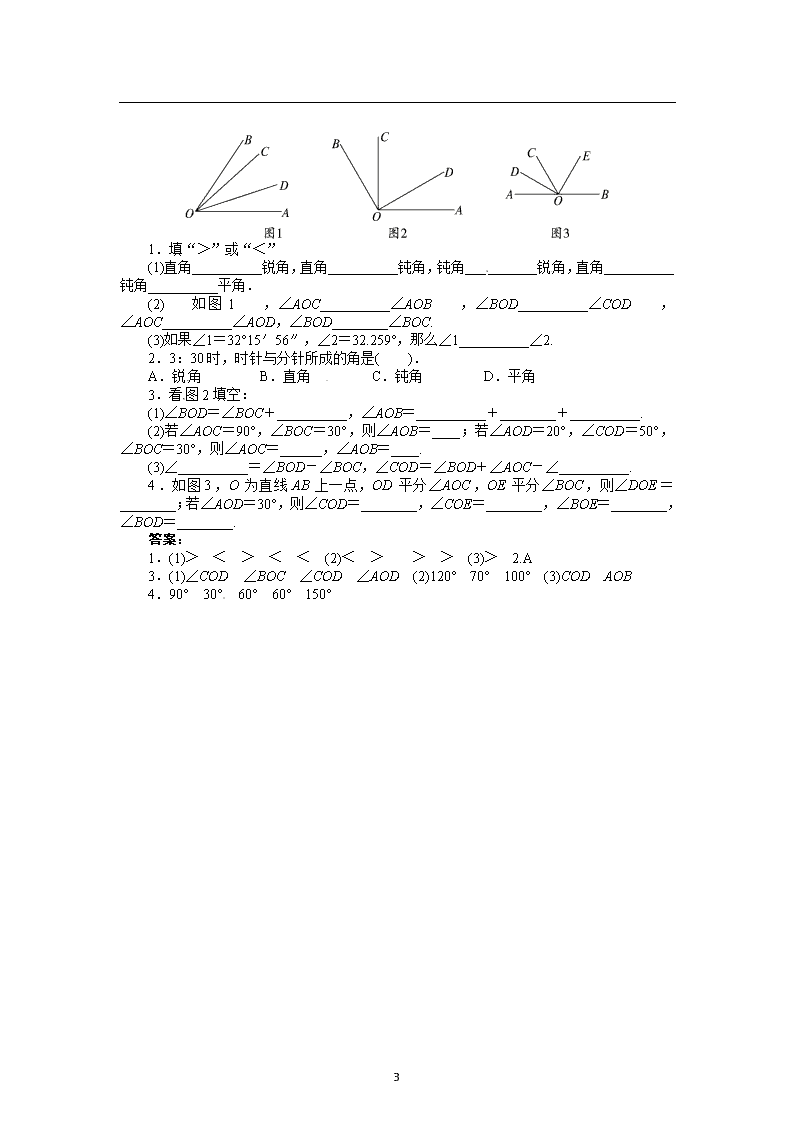请与同伴进行交流．‎ ‎【回答要点】‎ 比较角的大小，角的和、差、倍、分；角的平分线以及补角、余角的概念和性质．会用类比的思想方法．‎ 五、习题超市 3‎ ‎ ‎ ‎1．填“＞”或“＜”‎ ‎(1)直角__________锐角，直角__________钝角，钝角__________锐角，直角__________钝角__________平角．‎ ‎(2)如图1，∠AOC__________∠AOB，∠BOD__________∠COD，∠AOC__________∠AOD，∠BOD________∠BOC.‎ ‎(3)如果∠1＝32°15′56″，∠2＝32.259°，那么∠1__________∠2.‎ ‎2．3：30时，时针与分针所成的角是(　　)．‎ A．锐角 B．直角 C．钝角 D．平角 ‎3．看图2填空：‎ ‎(1)∠BOD＝∠BOC＋__________，∠AOB＝__________＋________＋__________.‎ ‎(2)若∠AOC＝90°，∠BOC＝30°，则∠AOB＝____；若∠AOD＝20°，∠COD＝50°，∠BOC＝30°，则∠AOC＝______，∠AOB＝____.‎ ‎(3)∠__________＝∠BOD－∠BOC，∠COD＝∠BOD＋∠AOC－∠__________.‎ ‎4．如图3，O为直线AB上一点，OD平分∠AOC，OE平分∠BOC，则∠DOE＝________；若∠AOD＝30°，则∠COD＝________，∠COE＝________，∠BOE＝________，∠BOD＝________.‎ 答案：‎ ‎1．(1)＞　＜　＞　＜　＜　(2)＜　＞　　＞　＞　(3)＞　2.A ‎3．(1)∠COD　∠BOC　∠COD　∠AOD　(2)120°　70°　100°　(3)COD　AOB ‎4．90°　30°　60°　60°　150°‎ 3‎