北京市丰台区2011-2012学年度第二学期初三综合数学练习（一） 10页

北京市丰台区2011-2012学年度第二学期初三综合练习（一）‎ ‎ 数 学 试 卷 ‎ 学校 　　　 姓名 准考证号 ‎ 考生须知 ‎1．本试卷共6页，共五道大题，25道小题，满分120分。考试时间120分钟。‎ ‎2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。‎ ‎3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。‎ ‎4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5．考试结束，将本试卷、答题卡和草稿纸一并交回。‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的．‎ ‎1．的相反数是 ‎ A． B． C． D． ‎ ‎2．据统计，今年北京市中考报名确认考生人数是96 200人，用科学记数法表示96 200为 ‎ A． B． C． D． ‎ ‎3．下列图形中，是正方体的平面展开图的是 ‎ ‎ ‎ A． B． C． D． ‎ ‎4．在一个不透明的口袋中，装有个红球和个白球，它们除颜色外完全相同，从口袋 中任意摸出一个球，摸到红球的概率是 ‎ A． B． C． D． ‎ 5． 如图，AB是⊙O的弦，OC是⊙O的半径，OC⊥AB于点D，若 AB=， OD=3，则⊙O的半径等于 A． B． C． D．‎ ‎6．2012年4月21日8时北京市部分区县的可吸入颗粒物数值统计如下表：‎ 区 县 东城 西城 海淀 朝阳 丰台 大兴 延庆 昌平 可吸入颗粒物（mg/m3）‎ ‎0.15‎ ‎0.15‎ ‎0.15‎ ‎0.15‎ ‎0.18‎ ‎0.18‎ ‎0.03‎ ‎0.14‎ 则这8个区县该日这一时刻的可吸入颗粒物数值的众数和中位数分别是 A．0.15和 0.14 B．0.18和0.15 C．0.15和0.15 D． 0.18和0.14 ‎ ‎7．若抛物线的最低点的纵坐标为n，则m-n的值是 A． B． C．1 D．2‎ 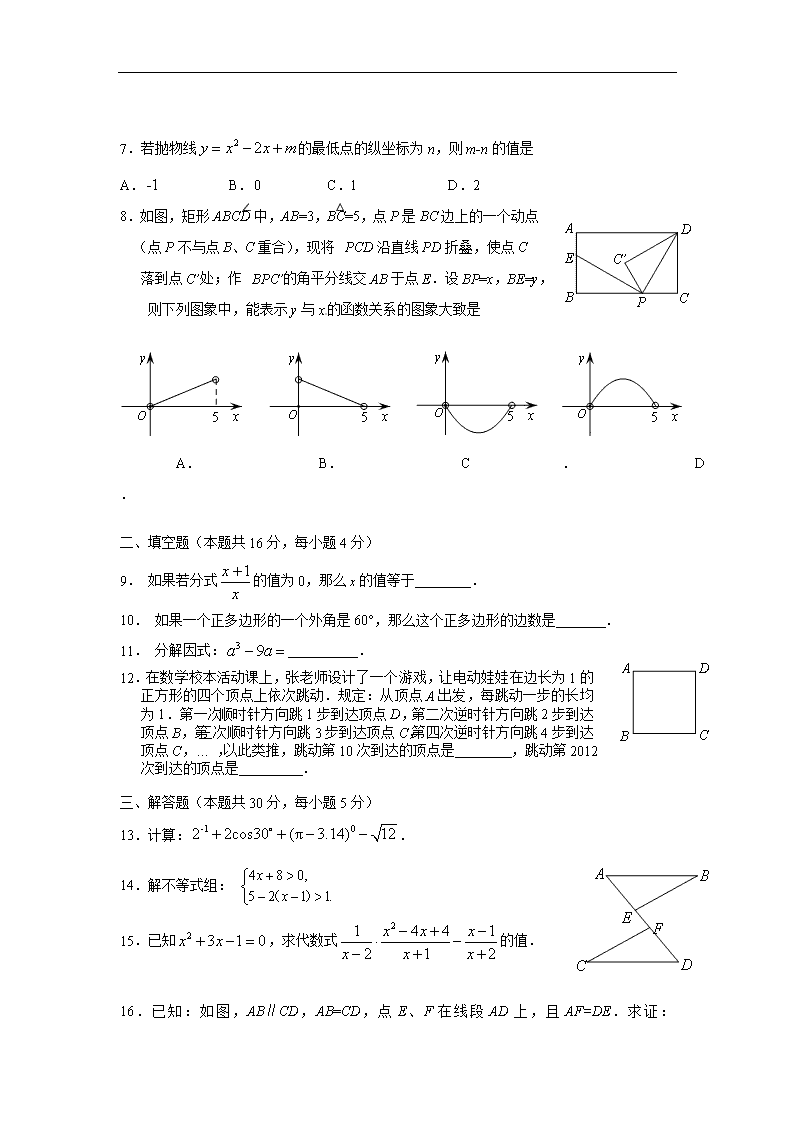8． 如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点 （点P不与点B、C重合），现将△PCD沿直线PD折叠，使点C 落到点C’处；作∠BPC’的角平分线交AB于点E．设BP=x，BE=y， 则下列图象中，能表示y与x的函数关系的图象大致是 A． B． C． D．‎ 二、填空题（本题共16分，每小题4分）‎ ‎9． 如果若分式的值为0，那么的值等于 ．‎ ‎10． 如果一个正多边形的一个外角是60°，那么这个正多边形的边数是 ．‎ ‎11． 分解因式： ．‎ ‎12．在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点A出发，每跳动一步的长均为1．第一次顺时针方向跳1步到达顶点D，第二次逆时针方向跳2步到达顶点B，第三次顺时针方向跳3步到达顶点C，第四次逆时针方向跳4步到达顶点C，… ，以此类推，跳动第10次到达的顶点是 ，跳动第2012次到达的顶点是 ．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：． ‎ ‎14．解不等式组： ‎ ‎15．已知，求代数式的值．‎ ‎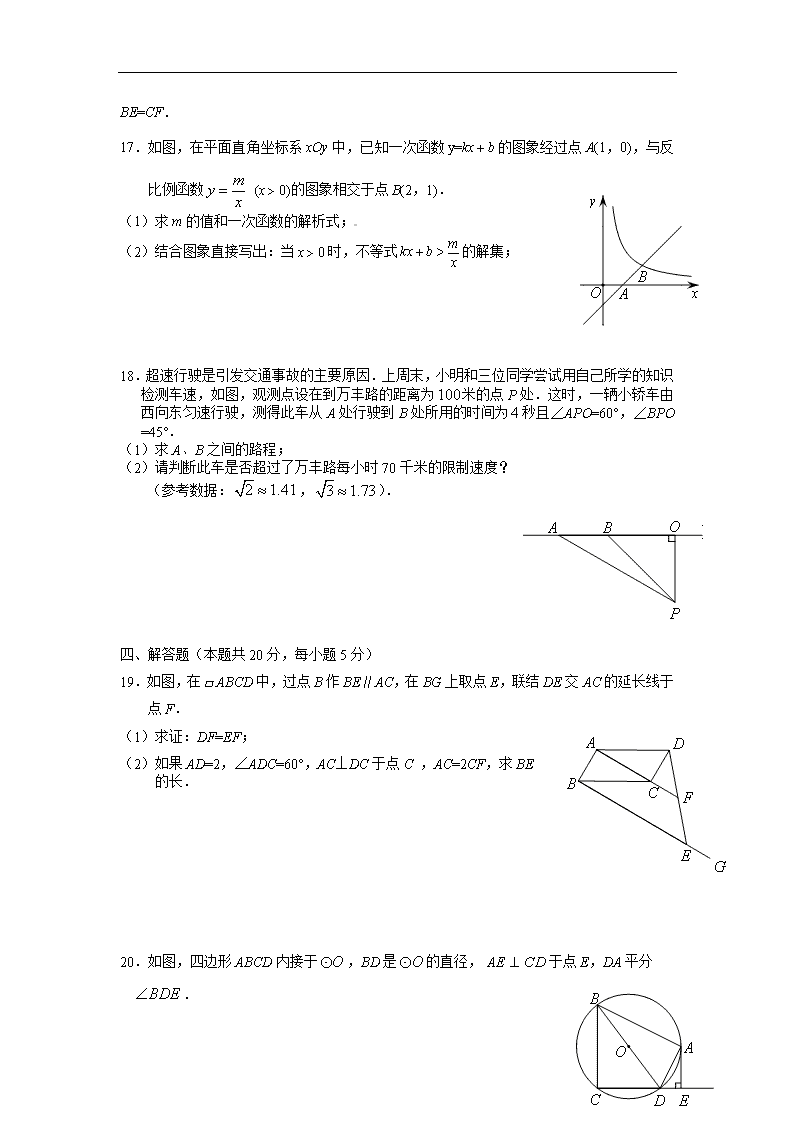16．已知：如图，AB∥CD，AB=CD，点E、F在线段AD上，且AF=DE．求证：‎ BE=CF．‎ ‎17．如图，在平面直角坐标系xOy中，已知一次函数的图象经过点A(1，0)，与反比例函数 (x0)的图象相交于点B(2，1)．‎ ‎（1）求m的值和一次函数的解析式；‎ ‎（2）结合图象直接写出：当x0时，不等式的解集；‎ ‎18．超速行驶是引发交通事故的主要原因．上周末，小明和三位同学尝试用自己所学的知识检测车速，如图，观测点设在到万丰路的距离为米的点P处．这时，一辆小轿车由西向东匀速行驶，测得此车从A处行驶到B处所用的时间为秒且∠APO=60°，∠BPO =45°． ‎ ‎（1）求A、B之间的路程；‎ ‎（2）请判断此车是否超过了万丰路每小时70千米的限制速度？‎ ‎（参考数据：，）．‎ 四、解答题（本题共20分，每小题5分）‎ ‎19．如图，在ABCD中，过点B作BE∥AC，在BG上取点E，联结DE交AC的延长线于点F．‎ ‎（1）求证：DF=EF；‎ ‎（2）如果AD=2，∠ADC=60°，AC⊥DC于点C ，AC=2CF，求BE 的长．‎ ‎[来源:学科网ZXXK]‎ ‎20．如图，四边形ABCD内接于，BD是的直径，于点E，DA平分 ．‎ ‎（1）求证：AE是的切线；‎ ‎（2）如果AB=，AE=2，求的半径．‎ ‎21．某学校为了解九年级学生的体育达标情况，从九年级学生中随机抽取若干名学生进行体 育测试，根据收集的数据绘制成如下统计图（图1、图2），请根据图中的信息解答下列问题：‎ ‎（1）补全图1与图2；‎ ‎（2）若该学校九年级共有400名学生，根据统计结果可以估计九年级体育达标优秀和良好的学生共有___________名．‎ 九年级学生体育测试成绩条形统计图 九年级学生体育测试成绩扇形统计图 ‎ % ‎ ‎5%‎ ‎ % ‎ ‎20%‎ ‎20%‎ ‎22．将矩形纸片分别沿两条不同的直线剪两刀，可以使剪得的三块纸片恰能拼成一个等腰三 角形（不能有重叠和缝隙）．‎ 小明的做法是：如图1所示，在矩形ABCD中，分别取AD、AB、CD的中点P、E、 F，并沿直线PE 、PF剪两刀，所得的三部分可拼成等腰三角形△PMN (如图2)． ‎ ‎（1）在图3中画出另一种剪拼成等腰三角形的示意图；‎ ‎（2）以矩形ABCD的顶点B为原点，BC所在直线为x轴建立平面直角坐标系（如图4）， 矩形ABCD剪拼后得到等腰三角形△PMN，点P在边AD上（不与点A、D重合），点M、N在x轴上（点M在N的左边）．如果点D的坐标为(5,8)，直线PM的解析式为，则所有满足条件的k的值为 ． ‎ ‎ ‎ ‎ ‎ 图1 图2 图3 ‎ ‎ ‎ ‎[来源:Z§xx§k.Com]‎ 图4 备用 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．已知：关于x的一元二次方程：.‎ ‎（1）求证：这个方程有两个不相等的实数根；‎ ‎（2）当抛物线与x轴的交点位于原点的两侧，且到原点的距离相等时， 求此抛物线的解析式；‎ ‎（3）将（2）中的抛物线在x轴下方的部分沿x轴翻折，其余部分保持能够不变，得到图形C1,将图形C1向右平移一个单位,得到图形C2，当直线(b<0)与图形C2恰有两个公共点时，写出b的取值范围. ‎ ‎24．已知：△ABC和△ADE是两个不全等的等腰直角三角形，其中BA=BC，DA=DE，联结EC，取EC的中点M，联结BM和DM．‎ ‎（1）如图1，如果点D、E分别在边AC、AB上，那么BM、DM的数量关系与位置关系是 ； ‎ ‎（2）将图1中的△ADE绕点A旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由． ‎ ‎ ‎ ‎25．已知：如图，在平面直角坐标系xOy中，以点P（2，）为圆心的圆与y轴相切于 点A，与x轴相交于B、C两点（点B在点C的左边）．‎ ‎（1）求经过A、B、C三点的抛物线的解析式；‎ ‎（2）在（1）中的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的．如果 存在，请直接写出所有满足条件的M点的坐标；如果若不存在，请说明理由；‎ ‎（3）如果一个动点D自点P出发，先到达y轴上的某点，再 到达x轴上某点，最后运动到（1）中抛物线的顶点Q 处，求使点D运动的总路径最短的路径的长．.‎ ‎7.北京市丰台区2011-2012学年度第二学期初三综合练习（一）参考答案 ‎ 一、选择题（本题共32分，每小题4分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 D C[来源:Z*xx*k.Com]‎ B A B C C D 二、填空题（本题共16分，每小题4分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎-1‎ ‎6‎ ‎ ‎ B；C 三、解答题（本题共30分，每小题5分）‎ ‎13．解：原式=…4分 ‎ = =．...5分 ‎ ‎14．解：由①得 ．…………1分 ‎ 由②得 ．‎ 解得．…………3分[来源:学科网]‎ ‎ 原不等式组的解集为．…….5分 ‎15．解： ‎ ‎ =………1分 ‎ =……2分 ‎==‎ ‎ =．…….3分 ‎，．……‎ ‎16．证明: AF=DE， AF-EF=DE –EF．‎ ‎ 即 AE=DF．………………1分 ‎ AB∥CD，∠A=∠D．……2分 ‎ 在△ABE和△DCF中 ，‎ ‎ AB=CD，‎ ‎ ∠A=∠D，‎ ‎ AE=DF．‎ ‎ △ABE ≌△DCF．……….4分 ‎ BE=CF．…………….5分 ‎17．解：（1）反比例函数 (x0)的图象经过点B(2，1) ，‎ ‎ ．………1分 ‎ 一次函数的图象经过点A(1，0)、 B(2，1)两点，‎ ‎ 解得………3分 ‎ 一次函数的解析式为．……4分 ‎（2）x2．………………………5分 ‎4分 ‎∴原式=．…….5分 ‎18．解：（1）在Rt△BOP中 ，∠BOP=90°，‎ ‎ ∠BPO =45°，OP =100，‎ ‎ OB=OP =100．………1分 ‎ 在Rt△AOP中， ∠AOP=90°，‎ ‎ ∠APO =60°，‎ ‎ ． ‎ ‎ ．…2分 ‎ (米)．…3分 ‎(2) ……4分 ‎(米/秒) ．‎ ‎18.25米‎/秒 =65.7千米/小时．‎ ‎ ，‎ 此车没有超过限制速度．……5分 四、解答题（本题共20分，每小题5分）‎ ‎19． 解：联结BD交AC于点O．‎ ‎（1）∵□ABCD，‎ ‎ ∴OB=OD，…1分 ‎∵BG∥AF， ‎ ‎∴DF=EF. ……2分 ‎（2）∵AC⊥DC，∠ADC=60°，AD=2，‎ ‎ ∴AC=． ……3分 ‎∵OF是△DBE的中位线，‎ ‎∴BE= 2OF．.……4分 ‎ ∵OF= OC+CF,‎ ‎ ∴BE= 2OC+2CF．‎ ‎∵□ABCD， ∴AC=2OC．‎ ‎∵AC=2CF，‎ ‎ ∴BE= ‎2AC=．…… 5分 20． ‎（1）证明：联结OA，‎ ‎∵OA=OD，‎ ‎∴∠1=∠2．‎ ‎∵DA平分，‎ ‎∴∠2=∠3．‎ ‎∴∠1=∠3．∴OA∥DE．……1分 ‎∴∠OAE=∠4，‎ ‎∵，∴∠4=90°．‎ ‎∴∠OAE=90°，即OA⊥AE．‎ 又∵点A在⊙O上，‎ ‎∴AE是⊙O的切线. ………2分 ‎（2）解：∵BD是⊙O的直径，‎ ‎∴∠BAD=90°．‎ ‎∵∠5=90°，∴∠BAD=∠5．‎ 又∵∠2=∠3，∴△BAD∽△AED．‎ ‎∴ ………3分 ‎∵BA=4，AE=2，∴BD=2AD． ‎ 在Rt△BAD中，根据勾股定理，‎ 得BD=．…………4分 ‎∴⊙O半径为．………5分 ‎21.解:（1）如图:………4分 ‎（2）300．………5分 ‎22．解：（1）如右图；…………………2分 ‎（2）．………5分 ‎ 图3‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23 .（1）证明∵．…………1分 ‎∴该方程总有两个不相等的实数根．. ………2分 ‎（2）由题意可知y轴是抛物线的对称轴， ∴，解得．………4分 ‎ ∴此抛物线的解析式为．.……5分 ‎9‎ ‎（3）-3