图形的对称 平移 旋转中考复习课件 36页

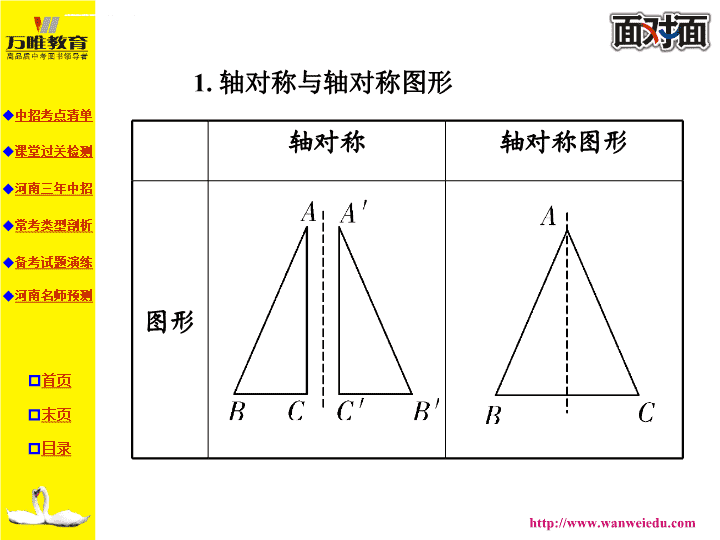
第一部分教材知识梳理第七章图形与变换第二节图形的对称、平移、旋转与位似\n中招考点清单考点一图形的对称（高频考点）【考情总结】近7年每年必考，三大题型均有涉及，考查的形式有：①单纯判断对称图形的识别考查2次；②利用对称图形的性质求点坐标考查3次；③利用折叠的对称性性质的相关计算与证明考查4次.\n1.轴对称与轴对称图形轴对称轴对称图形图形\n轴对称轴对称图形定义把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说明这两个图形关于这条直线（或轴）①_____，这条直线叫做②_______如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做③___________，这条直线就是它的④_______对称对称轴轴对称图形对称轴\n轴对称轴对称图形性质(1)成轴对称的两个图形全等；(2)成轴对称的两个图形只有一条对称轴；(3)对应点连线被对称轴垂直平分(1)对称轴有且至少有1条;(2)对称轴两旁的部分是全等图形;(3)对称轴两侧的对应点连线被对称轴垂直平分\n2.中心对称与中心对称图形中心对称中心对称图形图形\n中心对称中心对称图形定义把一个图形绕着某一点旋转⑤_____，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫⑥_________把一个图形绕着某一点旋转180°，如果旋转后的图形能够与原来的图形⑦____，那么这个图形叫做中心对称图形，这个点叫对称中心180°对称中心重合\n中心对称中心对称图形性质(1)成中心对称的两个图形全等；(2)成中心对称的两个图形只有一个对称中心；(3)对应点连线交于对称中心,并且被对称中心平分(1)对称中心有且只有1个;(2)对称中心平分中心对称图形内通过该点的任意线段\n3.常见的轴对称图形和中心对称图形(1)常见的轴对称图形：菱形、矩形、正方形、正六边形、圆等.(2)常见的中心对称图形：平行四边形、菱形、矩形、正方形、正六边形、圆等.(3)常见的既是轴对称图形又是中心对称图形：菱形、矩形、正方形、正六边形、圆等.\n考点二图形的平移【考情总结】近7年考查2次，其中2013年在填空题中结合抛物线的平移考查阴影部分面积，2011年在选择题中考查坐标系中图形经过旋转和平移变换求点坐标.\n1.图形的平移（1）定义：在平面内，将某个图形沿某个方向移动一定的⑧_____，这样的图形运动称为平移.（2）特征：（i）平移后，对应线段相等且平行,对应点所连的线段⑨_____且相等.（ii）平移后，对应角⑩_____且对应角的两边分别平行，方向相同.（iii）平移不改变图形的_____和大小，只改变图形的位置,平移后新旧两图形全等.距离平行相等形状11\n2.平移作图的基本步骤：（1）根据题意，确定平移的方向和平移距离；（2）找出原图形的关键点；（3）按平移方向和平移距离，平移各个关键点，得到各关键点的对应点；（4）按原图形依次连接得到的各关键点的对应点，得到平移后的图形.\n考点三图形的旋转（高频考点）【考情总结】近7年每年必考，三大题型均有涉及，涉及的考查形式有：①图形旋转与坐标系结合求点坐标考查3次；②图形旋转求阴影部分面积考查2次；③三角形旋转的证明与计算考查2次.\n1.定义：把一个平面图形绕着平面内某一点O转动一个角度，叫做图形的旋转，点O叫做_________，转动的角叫做旋转角.2.要素：旋转中心、_________、旋转角度.3.旋转的性质（1）对应点到旋转中心的距离_____；（2）对应点与旋转中心所连线段的夹角_____旋转角；（3）旋转前、后的图形_____.旋转中心12141316旋转方向相等15等于全等\n4.旋转作图的基本步骤：（1）根据题意，确定旋转中心、旋转方向、旋转角；（2）找出原图形的关键点；（3）连接关键点与旋转中心，按旋转方向与旋转角将它们旋转，得到各关键点的对应点；（4）按原图形依次连接得到的各关键点的对应点，得到旋转后的图形．\n考点四图形变换与坐标（高频考点）【考情总结】近7年从2008年～2011年连续考查4次，题型均为选择题，涉及的考查形式有：2008年利用轴对称图形性质求点坐标；2009年和2010年利用旋转的性质求点坐标；2011年旋转与平移结合求点坐标.若图形位置发生了平移、对称或旋转变换后，其各点坐标也相应改变：\n1.对于平移变换即图形形状、大小不变，只有位置发生改变，向右（左）平移，横坐标加（减）；向上（下）平移，纵坐标加（减）；2.对于对称变换，若图形关于x轴（y轴）对称，则纵（横）坐标乘-１，横（纵）坐标不变；图形关于原点对称，则横、纵坐标都乘-1；3.对于旋转变换，若旋转角为180°，则直接按中心对称性质求解，若旋转角为90°，可考虑用全等知识来计算.\n失分点12旋转后确定对应点坐标解决旋转后确定对应点坐标的题目往往需要先找准旋转的三要素即旋转中心、旋转角度及旋转方向，再通过旋转后的对应点向x轴、y轴作垂线，通过勾股定理求两条垂线段的长度来解决，以原点为旋转点的题目较为简单，以其他点为旋转点的题目可通过平移旋转点到原点，然后再平移回去的方法来解决，这种方法考查了转化思想.\n考点五图形的位似1.概念：如果两个多边形不仅相似，而且对应顶点的连线相交于一点，对应边互相平行，像这样的两个图形叫做位似图形，这个点叫做位似中心.这时我们说这两个图形关于这点位似，相似比叫做位似比.\n2.位似图形的性质(1)性质1：如果两个图形位似，那么任意一对对应点到位似中心的距离之比都等于位似比，任意一组对应边都互相平行(或在一条直线上)；(2)性质2：在平面直角坐标系中，如果以原点为位似中心，相似比为k，那么位似图形上的对应点的坐标的比等于k或-k.\n常考类型剖析类型一对称图形的识别例1(’14南京)下列图形中，既是轴对称图形，又是中心对称图形的是()C\n【解析】选项正误逐项分析A×是轴对称图形，不是中心对称图形B×是中心对称图形，不是轴对称图形C√既是轴对称图形，又是中心对称图形D×是轴对称图形，不是中心对称图形\n【方法指导】（1）判断一个图形是否是轴对称图形，要看是否沿某一条直线折叠后能与自身重合;（2）判断一个图形是否是中心对称图形，只要将其绕一点旋转180°后看能否与自身重合;(3)判断一个图形是否同时满足（1）（2）的条件时，即可判断一个图形是否既是轴对称图形，又是中心对称轴图形.\n拓展题1（’14哈尔滨）下列图形中，不是中心对称图形的是()B\n【解析】逐项分析如下：选项正误逐项分析A×既是轴对称图形，又是中心对称图形B√是轴对称图形，不是中心对称图形C×既是轴对称图形，又是中心对称图形D×既是轴对称图形，又是中心对称图形\n类型二图形变换与坐标例2（’14聊城改编)如图，在平面直角坐标系中，将△ABC绕点P旋转180°，得到△A1B1C1,则点A1的坐标为()A.(-4,-6)B.(-6,-4)C.(-2,-4)D.(-2,-6)A\n【解析】图形绕点P旋转180°，即△ABC与△A1B1C1关于点P中心对称，由此连接AP并延长到A1，使A1P＝AP.则点A1即为所求，通过作图可知点A1的坐标为（-4，-6）.\n拓展题2（’14苏州）如图，△AOB为等腰三角形，顶点A的坐标为(2,)，底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（）A.(,)B.(,)C.(,)D.(,)C\n【解析】如解图，过点A作AC⊥OB于C，过点O′作O′D⊥A′B于D，∵A(2，)，∴OC＝2，AC＝5，由勾股定理得，OA＝==3.∵△AOB为等腰三角形，OB是底边，∴OB=2OC＝2×2＝4，由旋转的性质得，BO′＝OB=4，∠A′BO′=∠ABO,∴Rt△ACB∽Rt△O′DB,∴拓展题2解图CD\n∴O′D=4×＝，BD=4×＝，∴OD=OB+BD＝4+＝，∴点O′的坐标为（，）.\n类型三图形旋转的相关计算例3（’14盐城）如图，在矩形ABCD中，AB＝3，AD＝1，把该矩形绕点A顺时针旋转α度得矩形AB′C′D′，点C′落在AB的延长线上，则图中阴影部分的面积是_________.\n【解析】∵在矩形ABCD中，AB＝，AD＝1，∴tan∠CAB==,AB=CD=,AD=BC=1,∴∠CAB=30°，∠BAB′=30°，∴S△AB′C′=×1×＝，S扇形BAB′＝＝，S阴影＝S△AB′C′-S扇形BAB′=.\n【方法指导】解决此题，应先观察图形，可知所求阴影部分面积为不规则图形面积，针对这种情形应采取和差法，将不规则图形转化为规则图形面积和差的形式进行求解；同时还要掌握矩形和旋转的性质，以及扇形面积和三角形面积的求法.\n拓展题3（’14陕西）如图，在正方形ABCD中，AD＝1.将△ABD绕点B顺时针旋转45°得到△A′BD′，此时A′D′与CD交于点E，则DE的长度为______.\n【解析】由旋转的性质可得BA′=BA=1，由正方形性质可得BD===,且∠BA′D′=∠A=90°，∠BDC=45°，∴A′D=-1,∴DE=（－1）=2－.\n