中考复习最短路径问题ppt课件 9页

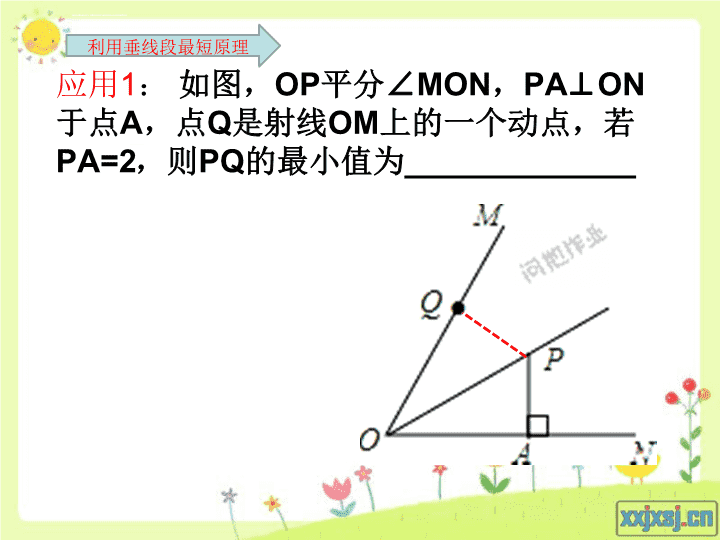
最短路径问题中考专题复习陈小文\n应用1：如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为_____________利用垂线段最短原理\n应用2：如图，圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上，问它爬行的最短路线长是多少？ABC解：将圆锥沿AB展开成扇形ABB’\n应用3：如右图是一个长方体木块，已知AB=3,BC=6,CD=2，假设一只蚂蚁在点A处，它要沿着木块表面爬到点D处，则蚂蚁爬行的最短路线长是__________。小结：不在同一个平面中两个顶点之间最短路径两个面展开成一个矩形，其邻边长有3种情况，分别是其中两边之和与第三边。如：（1）3+6，与2（2）6+2与3（3）3+2与6利用两点之间线段最短\n应用4:如图，正方形的边长为2，E为AB的中点，P是BD上一动点．连结AP、EP，则AP+EP的最小值是_______；P。P利用两点之间线段最短\n应用5：如图，抛物线y=x2-4x-5与x轴交于A，B两点，与y轴交于C点，且点D是抛物线的顶点，点M是x轴上的一个动点，当MC＋MD的值最小时，求点M的坐标。利用：两点之间线段最短\n应用5：如图，抛物线y=x2-4x-5与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．点M（m，0）是x轴上的一个动点，当MC＋MD的值最小时，求m的值分析：（方法1）作出点C关于x轴的对称点C′，连接C'D交x轴于点M，根据“两点之间，线段最短”可知MC＋MD的值最小．求出直线C'D的解析式，即可得出点M的坐标，进而求出m的值\n应用5：如图，抛物线y=x2-4x-5与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．点M（m，0）是x轴上的一个动点，当MC＋MD的值最小时，求m的值分析：（方法2）作出点C关于x轴的对称点C′，连接C'D交x轴于点M，根据“两点之间，线段最短”可知MC＋MD的值最小．利用三角形相似求解。\n1、利用“垂线段最短”原理（1）平面图形（作垂线段）（2）立体图形（先展开平面图形再作垂线段）2、利用“两点之间线段最短”原理（1）立体图形（先展开平面图形再连接两个点）课堂小结：（2）平面图形（直接连接两点或者构建对称模型）如何确定最短路径问题