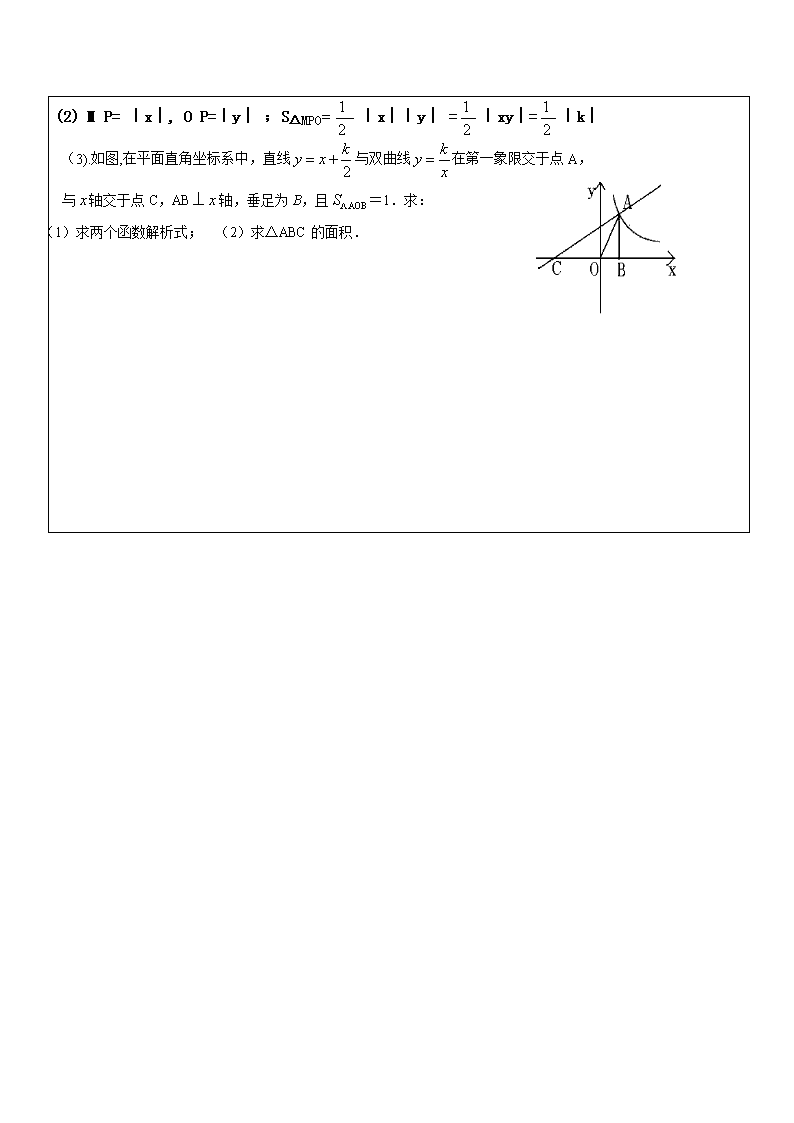初中反比例函数教案 3页

内容：反比例函数教学目的1、提高从函数图像中获取信息的能力；2、探索并掌握反比例函数的主要性质重难点重点：反比例函数的概念难点：反比例函数的图像与性质教学过程一、反比例函数的概念：知识要点：1、一般地，形如y=(k是常数,k=0)的函数叫做反比例函数。注意：（1）常数k称为比例系数，k是非零常数；（2）解析式有三种常见的表达形式：（A）y=（k≠0），（B）xy=k（k≠0）（C）y=kx-1（k≠0）例题讲解：有关反比例函数的解析式例1、（1）下列函数，①②.③④.⑤⑥；其中是y关于x的反比例函数的有：_________________。（2）函数是反比例函数，则的值是（　　）　A．－1　　　　　B．－2　　　　C．2　　　　D．2或－2（3）如果是的反比例函数，是的反比例函数，那么是的（　）A．反比例函数　B．正比例函数　C．一次函数　D．反比例或正比例函数练习：（1）如果是的正比例函数，是的反比例函数，那么是的（）（2）如果是的正比例函数，是的正比例函数，那么是的（）（4）反比例函数的图象经过（—2，5）和（，），求（1）的值；（2）判断点B（，）是否在这个函数图象上，并说明理由二、反比例函数的图象和性质：\n知识要点：1、形状：图象是双曲线。2、位置：（1）当k>0时,双曲线分别位于第________象限内；（2）当k<0时,双曲线分别位于第________象限内。3、增减性：（1）当k>0时,_________________,y随x的增大而________；（2）当k<0时,_________________,y随x的增大而______。4、变化趋势：双曲线无限接近于x、y轴,但永远不会与坐标轴相交5、对称性：（1）对于双曲线本身来说，它的两个分支关于直角坐标系原点____________；（2）对于k取互为相反数的两个反比例函数（如：y=和y=）来说，它们是关于__________。例题讲解：（一）反比例函数的图象和性质：例2、（1）写出一个反比例函数，使它的图象经过第二、四象限　　　　　　　　　　　　　．　（2）若反比例函数的图象在第二、四象限，则的值是（　　）A、－1或1;　B、小于的任意实数;C、－1;　　　Ｄ、不能确定OOOOBAD（3）已知，函数和函数在同一坐标系内的图象大致是（）C例3、（1）下列函数中，当时，随的增大而增大的是（　　）　A．　　　B．　　　C．　　　D．．（2）若点（，）、（，）和（，）分别在反比例函数的图象上，且　，则下列判断中正确的是（　　）　A．　　B．　C．　　D．（二）反比例函数与三角形面积结合题型。oyxyxoyxoyxoABCD例4、（1）矩形的面积为6cm2，那么它的长（cm）与宽（cm）之间的函数关系用图象表示为（）PM（x,y）（2）反比例函数y=(k>0)在第一象限内的图象如图,点M(x,y)是图象上一点,MP垂直x轴于点P,MQ垂直y轴于点Q；①如果矩形OPMQ的面积为2，则k=_________;②如果△MOP的面积=____________.总结：(1)点M(x,y)是双曲线上任意一点,则矩形OPMQ的面积是MP*MQ=︳x︱︳y︱=︳xy︱=︳k︱\n(2)MP=︳x︱,OP=︳y︱；S△MPO=︳x︱︳y︱=︳xy︱=︳k︱（3).如图,在平面直角坐标系中，直线与双曲线在第一象限交于点A，与轴交于点C，AB⊥轴，垂足为B，且＝1．求：（1）求两个函数解析式；　（2）求△ABC的面积．