【物理】2019届一轮复习人教版　牛顿运动定律在临界和极值问题中的应用学案 2页

第28点　牛顿运动定律在临界和极值问题中的应用 在某些物理情景中，物体运动状态变化的过程中，由于条件的变化，会出现两种状态的衔接，两种现象的分界，同时使某个物理量在特定状态时，具有最大值或最小值．这类问题称为临界、极值问题．‎ 临界极值问题是动力 的常见问题，常用的解决方法有：‎ ‎(1)极限法：在题目中如出现“最大”、“最小”、“刚好”等词语时，一般隐含着临界问题，处理这类问题时，可把物理问题(或过程)推向极端，从而使临界现象(或状态)显现出来，达到快速求解的目的．‎ ‎(2)假设法：有些物理过程中没有明显出现临界状态的线索，但在变化过程中有可能出现临界状态，也可能不出现临界状态，解答这类问题，一般用假设法．‎ ‎(3)数 方法：将物理过程转化为数 表达式，根据数 表达式求解得出临界条件．‎ 对点例题　一个质量为m的小球B，用两根等长的细绳1、2分别固定在车厢的A、C两点，如图1所示，已知两绳拉直时，两绳与车厢前壁的夹角均为45°.试求：‎ 图1‎ ‎(1)当车以加速度a1＝g向左做匀加速直线运动时1、2两绳的拉力的大小；‎ ‎(2)当车以加速度a2＝2g向左做匀加速直线运动时，1、2两绳的拉力的大小．‎ 解题指导　设当细绳2刚好拉直而无张力时，车的加速度为向左的a0，由牛顿第二定律得，F1cos 45°＝mg，F1sin 45°＝ma0，可得：a0＝g.‎ ‎(1)因a1＝ga0，故细绳1、2均张紧，设拉力分别为F12、F22，由牛顿第二定律得 解得：F12＝mg，F22＝mg.‎ 答案　(1)mg　0　(2)mg　mg 特别提醒　求解此类问题时，一定要找准临界点，从临界点入手分析物体的受力情况和运动情况，看哪些量达到了极值，然后对临界状态应用牛顿第二定律结合整体法、隔离法求解即可．‎ 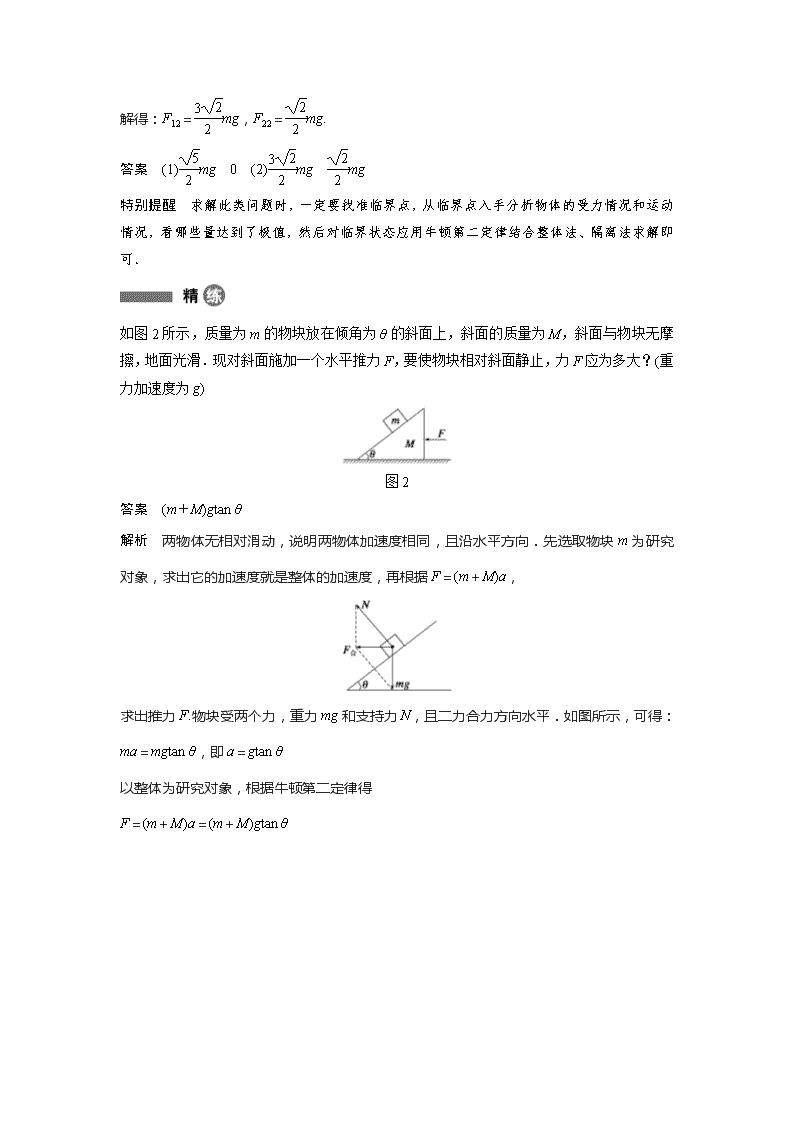如图2所示，质量为m的物块放在倾角为θ的斜面上，斜面的质量为M，斜面与物块无摩擦，地面光滑．现对斜面施加一个水平推力F，要使物块相对斜面静止，力F应为多大？(重力加速度为g)‎ 图2‎ 答案　(m＋M)gtan θ 解析　两物体无相对滑动，说明两物体加速度相同，且沿水平方向．先选取物块m为研究对象，求出它的加速度就是整体的加速度，再根据F＝(m＋M)a，‎ 求出推力F.物块受两个力，重力mg和支持力N，且二力合力方向水平．如图所示，可得：‎ ma＝mgtan θ，即a＝gtan θ 以整体为研究对象，根据牛顿第二定律得 F＝(m＋M)a＝(m＋M)gtan θ