[工学]电工学上册课件 38页

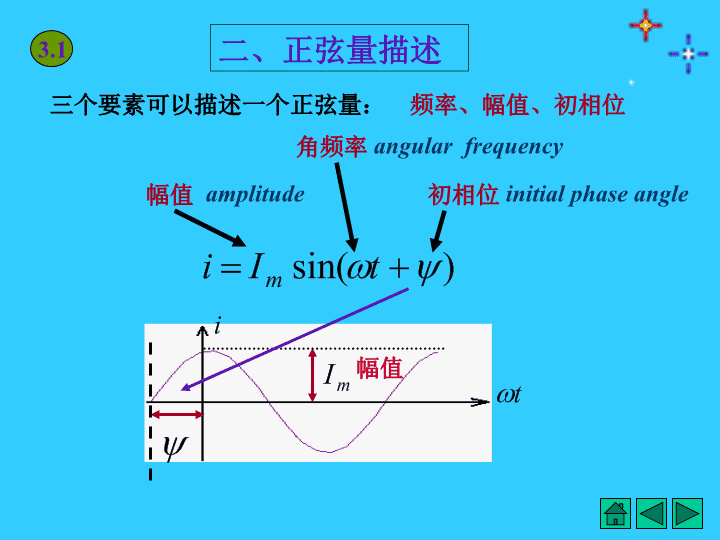
第三章正弦交流电路第一节正弦交流电的基本概念第二节正弦量的相量表示法第三节电阻元件的正弦交流电路第四节电感元件的正弦交流电路第五节电容元件的正弦交流电路第六节正弦稳态电路的分析第七节功率因数的提高第八节谐振电路小结与习题\n第三章正弦交流电路一、概念1、什么是正弦交流电：随时间按正弦函数规律周期性变化的电压、电流和电动势等物理量，通称为正弦量。它们在一个周期内平均值为零。2、为什么要使用交流电：交流电容易获得。3、交流电的正方向：实际方向与参考方向一致时取正。4、交、直流电路比较：①交、直流电的I、U、E、P具有相同的物理意义②基本定律定理一样，网络分析的方法理论一样。③交流电是变的，其瞬时值符合KCL、KVL，但有效值不符合。3.1§3-1正弦交流电路的基本概念\n二、正弦量描述角频率初相位幅值三个要素可以描述一个正弦量：频率、幅值、初相位幅值amplitudeangularfrequencyinitialphaseangle3.1\n2、幅值与有效值1、频率f（周期Τ、角频率ω）周期T：变化一周所需的时间，用sms表示。频率f：每秒重复变化的次数。单位：Hz赫(兹)f=1/T角频率ω：每秒变化的角度(弧度)，ω=2πf=2π/Trad/s幅值正弦量变化过程中呈现的最大值，电流Im，电压Um如果一个交流电流i通过一个电阻R，在一个周期内产生的热量为Q，而在相同的时间里产生相同的热量需通入直流电为I，则称I为i的有效值。即：I、U表示有效值Im、Um表示幅值有效值3.1\n初相位是0时刻到波形起始点那段距离对应的角度相位差两个同频正弦量相位角之差，表示为3、初相位与相位差3.1＜1800\n规定：|y|(180°)。特殊相位关系：tu,iuiOtu,iuiOtu,iuiOj=0同相j=(180o)反相=p/2正交3.1\n例3-1解：1）已知2）\n3.2§3-2正弦量的相量表示法1.相量图直角坐标系中有一有向线段相量图可以描述一个正弦量正弦量表示法瞬时值（三角函数）波形图相量图相量式（复数）直观，但不便于分析计算便于完成正弦量的加减乘除运算旋转起来投影#\n3.2已知：求：解：采用相量图法计算：瞬时值相加很繁琐结果：#正弦量相量图对应例\n3.2§3-2正弦量的相量表示法2.相量式（复数表示法）将相量图置于复平面中+1j实轴虚轴向实轴的投影复平面向虚轴的投影相量表示为相量式：代数形式：指数形式：极坐标形式其中#\n运算法则：(1)加减运算A1A2ReImO加减可用图解法3.2§3-2正弦量的相量表示法(2)乘除运算除法：模相除，角相减乘法：模相乘，角相加则:#若=|A1|1，若=|A2|2若=a1+jb1，=a2+jb2则±=(a1±a2)+j(b1±b2)\n3.2§3-2正弦量的相量表示法1.相量图正弦量表示法瞬时值（三角函数）波形图相量图相量式（复数）#正弦量相量图对应2.相量式（复数表示法）代数形式：指数形式：极坐标形式其中\n正弦电压与相量的对应关系：已知例1.试用相量表示i,u.解：例2.试写出电流的瞬时值表达式。解：3.2\n例3.解:例4.解：上式#3.2\n例5．同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态分析中有重要作用，尤其适用于定性分析。ReImReIm首尾相接#3.2\n§3-3电阻元件的正弦交流电路一.伏安关系URuR(t)i(t)RUR=RI相量模型R显然有1.电压与电流为同频正弦量2.有效值与相量均有欧姆定律成立二.功率有功功率三.相量图同相位#3.3\n§3-4电感元件的正弦交流电路一.伏安关系1.电压与电流为同频正弦量2.有效值与相量均符合欧姆定律3.感抗XL是频率f的函数4.电压超前电流900#3.4i(t)uL(t)LjL相量模型UL则设相量欧姆定律有效值欧姆定律称为感抗称为复感抗\n二.功率有功功率三.相量图3.4瞬时功率以2交变，有正有负，一周期内刚好互相抵消。itOuLpL波形图2P=0u与i相位相差900#无功功率Q无功功率是指储能元件与电源间进行能量交换的那部分功率乏(Var)\n§3-5电容元件的正弦交流电路一.伏安关系1.电压与电流为同频正弦量2.有效值与相量均符合欧姆定律3.感抗XC是频率f的函数4.电流超前电压9003.5则设相量欧姆定律有效值欧姆定律称为容抗复容抗i(t)u(t)C相量模型\n二.功率三.相量图3.5瞬时功率以2交变，有正有负，一周期内刚好互相抵消。utOipc波形图：2u与i相位相差900#无功功率是指储能元件与电源间进行能量交换的那部分功率乏(Var)P=0有功功率无功功率Q\n§3-6正弦稳态电路的分析1.RC串联电路|Z|RXCj阻抗三角形阻抗模阻抗角iuCRR相量模型称为复阻抗相量模型法3.6#\n§3-6正弦稳态电路的分析1.RC串联电路R相量图法选电路的共量作为参考相量然后依次画出、、3.6相量图为一直角三角形这种方法可将复杂的正弦电路计算转化为平面几何的分析计算各边长为对应量的有效值UR=3VUC=4V如：U=？5V#电压三角形\n§3-6正弦稳态电路的分析1.RC串联电路功率问题3.6#RC电阻消耗的有功功率电路总有功功率=电路总无功功率=储能元件上的无功功率电路视在功率●●●PQS视在功率wVarVA功率三角形\n§3-6正弦稳态电路的分析2.RLC串联电路3.6#RLC电路总阻抗电压三角形是电压与电流的相位差，也是阻抗角电压超前电流电路呈感性\n§3-6正弦稳态电路的分析2.RLC串联电路3.6#RLC对于电压三角形各边电压有效值乘以电流有效值分别变为有功功率P、无功功率Q、视在功率SPSQ●●●功率三角形\n关于交流电路的功率有功，无功，视在功率的关系：有功功率:P=UIcosj单位：W无功功率:P=UIsinj单位：var视在功率:S=UI单位：VAjSPQjZRXjUURUXRX+_+_ºº+_功率三角形阻抗三角形电压三角形3.视在功率(表观功率)反映电气设备的容量。2.无功功率Q表示交换功率的最大值var(乏)1.有功功率PP=UIcosj(W)表示电路真正消耗的功率\n电感、电容的无功补偿作用LCRuuLuCi+-+-+-当L发出功率时，C刚好吸收功率，则与外电路交换功率为pL+pC。因此，L、C的无功具有互相补偿的作用。关于交流电路的功率tiOuLuCpLpC\n例1LCRuuLuCi+-+-+-已知：R=15,L=0.3mH,C=0.2F,求i,uR,uL,uC.解：其相量模型为jLR+-+-+-分电压大于总电压-3.4°相量图\n例2：已知Z1=10+j6.28,Z2=20-j31.9,Z3=15+j15.7。Z1Z2Z3ab求Zab。\n负载消耗多少有功功率由负载的阻抗角决定。P=Scosjcosj=1,P=Scosj=0.7,P=0.7S一般用户为感性负载异步电动机、日光灯(1)电源的利用率降低。电流到了额定值，但功率容量还有(2)线路压降损耗和能量损耗增大。I=P/(Ucosj)§3-7功率因数提高负载电源客观事实功率因数低带来的问题j1\n在负载两端并联电容，提高功率因数分析:j1j2并联电容后,原感性负载取用的电流不变,吸收的有功无功都不变，即负载工作状态没有发生任何变化。由于并联电容的电流领先总电流，从相量图上看,UI的夹角减小了,从而提高了电源端的功率因数cosφ解决办法LRC+_原负载新负载并联电容后，原负载的任何参数都没有改变！\n补偿容量的确定j1j2代入补偿容量不同全——不要求(电容设备投资增加,经济效果不明显)欠过——使功率因数又由高变低(性质不同)综合考虑，提高到适当值为宜(0.9左右)。LRC+_补偿后电流？补偿后功率因数？\n补偿容量也可以用功率三角形确定：j1j2PQCQLQ思考：能否用串联电容提高cosj?单纯从提高cosj看是可以，但是负载上电压改变了。在电网与电网连接上有用这种方法的，一般用户采用并联电容。\n功率因数提高后，线路上电流减少，就可以带更多的负载，充分利用设备的能力。再从功率这个角度来看:并联C后，电源向负载输送的有功UILcosj1=UIcosj2不变，但是电源向负载输送的无功UIsinj2