热工学基础12 39页

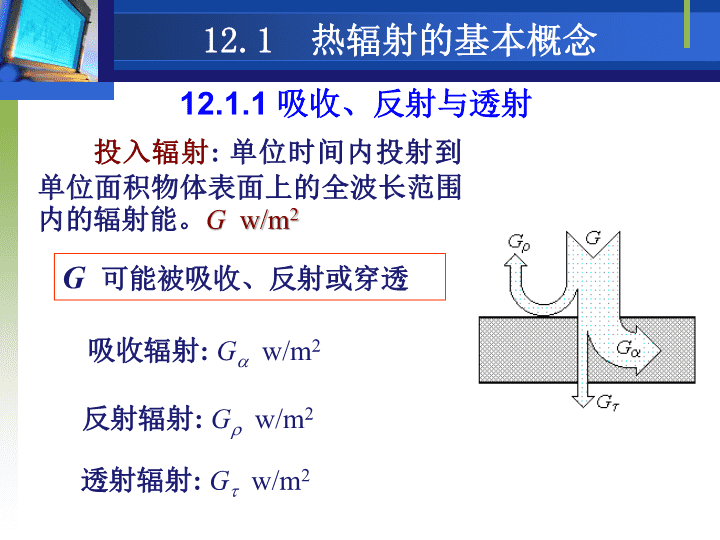
第十二章辐射换热\n本章主要内容辐射换热的基本概念辐射换热基本定律辐射换热的计算方法\n12.1热辐射的基本概念12.1.1吸收、反射与透射投入辐射:单位时间内投射到单位面积物体表面上的全波长范围内的辐射能。Gw/m2反射辐射:Gw/m2吸收辐射:Gw/m2透射辐射:Gw/m2G可能被吸收、反射或穿透\n吸收比反射比透射比根据能量守恒，如果投入辐射是某一波长的辐射能G，则光谱吸收比光谱反射比光谱透射比12.1热辐射的基本概念12.1.1吸收、反射与透射\n注意两点（1）属于物体的辐射特性，取决于物体的种类、温度和表面状况，是波长的函数。不仅取决于物体的性质，还与投射辐射能的波长分布有关。（2）固体和液体对辐射能的吸收和反射基本上属于表面效应（1μm-1mm)。（3）对于气体τ=0ρ=0\n举例冬天，隔着玻璃晒太阳感觉更暖和，为什么？普通玻璃对太阳辐射的光几乎完全穿透，而对常温下室内物体的红外辐射热量被阻挡在房间内，这一现象类似与“温室效应”。海水的颜色为什么总是蓝色的？海水对不同波长的可见光吸收率不同，对蓝色波长附近的射线吸收少，反射多，所以呈蓝色。\n镜反射与漫反射产生何种反射决于物体表面的粗糙尺度和投射辐射能的波长。(a)镜反射(b)漫反射绝大数工程材料对热辐射的反射都近似漫反射。\n12.1.2灰体与黑体灰体：光谱辐射特性不随波长而变化的假想物体，即分别等于常数。工程常见的温度范围（≤2000K)内，，一般工程材料的光谱吸收比基本与波长无关，所以工业上的辐射传热计算一般都按灰体处理。\n注意：黑体、白体与黑色、白色物体的区别。人工黑体模型镜体（白体）：=1绝对透明体：=1绝对黑体：12.1.2灰体与黑体吸收比=1的物体，简称黑体。黑体和灰体一样，是一种理想物体。\n福建永定客家土楼\n12.1.3辐射强度立体角：半径为r的球面上面积A与球心所对应的空间角度。其大小为：单位为Sr（球面度），半球空间立体角为2sr立体角在球面上所围的面积与半径的平方成正比。辐射强度说明物体表面在空间某个方向上发射辐射能的多少。\n辐射强度：单位时间内从单位投影面积（可见面积）所发出的包含在单位立体角内的辐射能。称为dA1在（，）方向的辐射强度，或称为定向辐射强度，单位是W/(m2Sr)。12.1.3辐射强度dA1向dA2发射的辐射能为dΦ，dA1在θ方向的投影面积为dA1cosθ\n辐射强度的大小不仅取决于物体种类、表面性质、温度，还与方向有关。对于各向同性的物体表面，辐射强度与经度角无关,对某一波长辐射能而言的辐射强度。光谱辐射强度：辐射强度与光谱辐射强度之间的关系光谱辐射强度的单位为W/(m3Sr)或W/(m2mSr)。12.1.3辐射强度\n12.1.4辐射力在单位时间内，每单位面积表面向其上半球空间发射的全部波长的辐射能。用E表示，单位为W/m2。黑体的辐射力Eb.光谱辐射力：某一波长辐射能的辐射力用E表示，单位为W/m3。辐射力与光谱辐射力之间的关系定向辐射力：在单位时间内，单位面积表面向某方向发射的单位立体角内的辐射能。用E表示，单位为W/(m2sr)。\n定向辐射力与辐射力之间的关系：定向辐射力与辐射强度之间的关系：辐射力与辐射强度之间的关系：12.1.4辐射力E--辐射力Eb--黑体辐射力Eλ--光谱辐射力Eθ--定向辐射力\n12.2黑体辐射的基本定律1.普朗克（M.Planck）定律2.斯忒藩—玻耳兹曼(Stefan-Boltzmann)定律3.兰贝特（Lambert）定律\n12.2.1普朗克定律C1=3.743×10-16Wm2;C2=1.439×10-2mK。1901年普朗克提出的黑体辐射能按波长的分布规律该定律给出了黑体光谱辐射力随波长和温度的函数关系：\n12.2.1普朗克定律特点：（1）温度愈高，同一波长下的光谱辐射力愈大；（2）在一定的温度下，黑体的光谱辐射力在某一波长下具有最大值；（3）随着温度的升高，Eb取得最大值的波长max愈来愈小，即在坐标中的位置向短波方向移动。\n维恩（Wien）位移定律12.2.1普朗克定律对最大的Ebλ的波长λmax与温度T存在关系室温下呈黑色的铁棒在炉中加热时，颜色渐呈暗红、红、橙黄，为什么？随着铁棒加热，温度升高。其辐射能量最大波长向短波方向移动，即经历了由远红外线、近红外线到可见光的区域，因而会呈现上述颜色的变化。\n12.2.2斯忒藩—玻耳兹曼定律斯忒藩—玻耳兹曼定律表达式：式中=5.67×10-8W/(m2K4)，称为斯忒藩—玻耳兹曼常数，又称为黑体辐射常数。（四次方定律）斯忒藩—玻耳兹曼定律表达式可直接由下式导出：\n波段辐射力波段辐射力占黑体辐射力Eb的百分数12.2.2斯忒藩—玻耳兹曼定律\n称为黑体辐射函数，表示温度为T的黑体所发射的辐射能中在波段（0～）内的辐射能所占的百分数。根据普朗克定律表达式利用黑体辐射函数数值表(p241表12-1)可以很容易地用下式计算黑体在某一温度下发射的任意波段的辐射能量。12.2.2斯忒藩—玻耳兹曼定律\n12.2.3兰贝特定律兰贝特定律:黑体的辐射强度与方向无关，半球空间各方向上的辐射强度都相等。漫发射体空间各个方向上辐射强度都相等的物体。此时，漫射体的辐射强度类似于灯泡的亮度，即从任何方向看过去亮度相同。根据定向辐射力与辐射强度的关系兰贝特定律也称为余弦定律\n三大定律小结1、四次方定律：描述黑体在某一温度下向半球空间所有方向辐射的全部波长的能量，即对方向和波长都积分的结果；2、普朗克定律：描述黑体在某一温度下向半球空间所有方向辐射的能量沿波长分布的规律，即只对方向积分，但研究的是某一波长；3、兰贝特（Lambert）定律：描述黑体在某一温度下所辐射的全部波长的能量沿半球空间方向上的分布规律，即只对波长积分，但研究的是某一方向。对黑体而言，辐射强度是常数。\n12.3实际物体的辐射特性与基尔霍夫定律12.3.1实际物体的发射特性发射率（黑度）：发射率反映了物体发射辐射能的能力的大小。光谱发射率（光谱黑度）：发射率与光谱发射率之间的关系为对于灰体，＝常数，同温度\n实际物体的辐射力实际物体的辐射力并不严格遵循四次方定律，所存在的偏差包含在由实验确定的发射率数值之中。定向发射率（定向黑度）：实际物体不是漫发射体，定向发射率是方向角的函数。12.3.1实际物体的发射特性\n12.3.2实际物体的吸收特性实际物体的光谱吸收比也与黑体、灰体不同，是波长的函数。几种金属材料的光谱吸收比\n几种非金属材料的光谱吸收比辐射特性随波长变化的性质称为辐射特性对波长的选择性。实际物体的吸收比不仅取决于物体本身材料的种类、温度及表面性质，还和投入辐射的波长分布有关，因此和投入辐射能的发射体温度有关。12.3.2实际物体的吸收特性\n12.3.3基尔霍夫（G.R.Kirchhoff）定律基尔霍夫定律揭示了物体吸收辐射能的能力与发射辐射能的能力之间的关系，其表达式为说明吸收辐射能能力愈强的物体的发射辐射能的能力也愈强。在温度相同的物体中，黑体吸收辐射能的能力最强，发射辐射能的能力也最强。对于漫射、灰体，辐射特性与波长无关，\n12.4辐射换热的计算方法基本假设：（1）进行辐射换热的物体表面之间是不参与辐射的介质(单原子或结构对称的双原子气体、空气)或真空；（2）每个表面都是漫射、灰体或黑体表面；（3）每个表面的温度、辐射特性及投入辐射分布均匀。任意放置的两黑体表面之间的辐射换热表面1发出的辐射能表面2发出的辐射能A1T1A2T2\n12.4辐射换热的计算方法表面1发出的辐射能落到表面2上的百分数表示为：表面2发出的辐射能落到表面1上的百分数表示为：X1,2称为表面1对表面2的角系数X1,2称为表面1对表面2的角系数A1T1A2T2\n12.4辐射换热的计算方法由于是黑体，能吸收落到其表面上的全部能量两表面间的净换热量如果两表面处于热平衡，T1=T2两表面间的净换热量Φ1,2=0,1、定义从表面1发出的总辐射能中落到表面2上份额称为表面1对表面2的角系数，用符号X1,2表示。\n2.角系数的性质1）相对性（互换性）：2）完整性：（由n个表面组成的封闭系统）非凹表面：Xi,i=0角系数是纯几何量，只取决于两个物体表面的几何形状、大小和相对位置。角系数的基本属性：\n3）角系数的可加性：3.角系数的计算方法有积分法、代数法、图解法(或投影法)等1）积分法：根据角系数表达式通过积分运算求得角系数2.角系数的性质\n2）代数法：利用角系数的定义及性质,通过代数运算确定角系数。3.角系数的计算方法三个非凹表面构成的封闭空腔完整性：相对性：六个未知量，六个方程，方程组可解。\n3.角系数的计算方法\n交叉线法根据角系数的完整性，有：其中：则：文字表述：3.角系数的计算方法\n第十二章小结重点掌握以下内容：（1）基本概念：吸收比、反射比、透射比、黑体、灰体、漫射体、辐射强度、辐射力、发射率（黑度）、角系数等；（2）基本定律：普朗克定律、斯忒藩—玻耳兹曼定律、维恩位移定律、兰贝特定律、基尔霍夫定律；\n本章结束