- 814.00 KB
- 2022-08-09 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
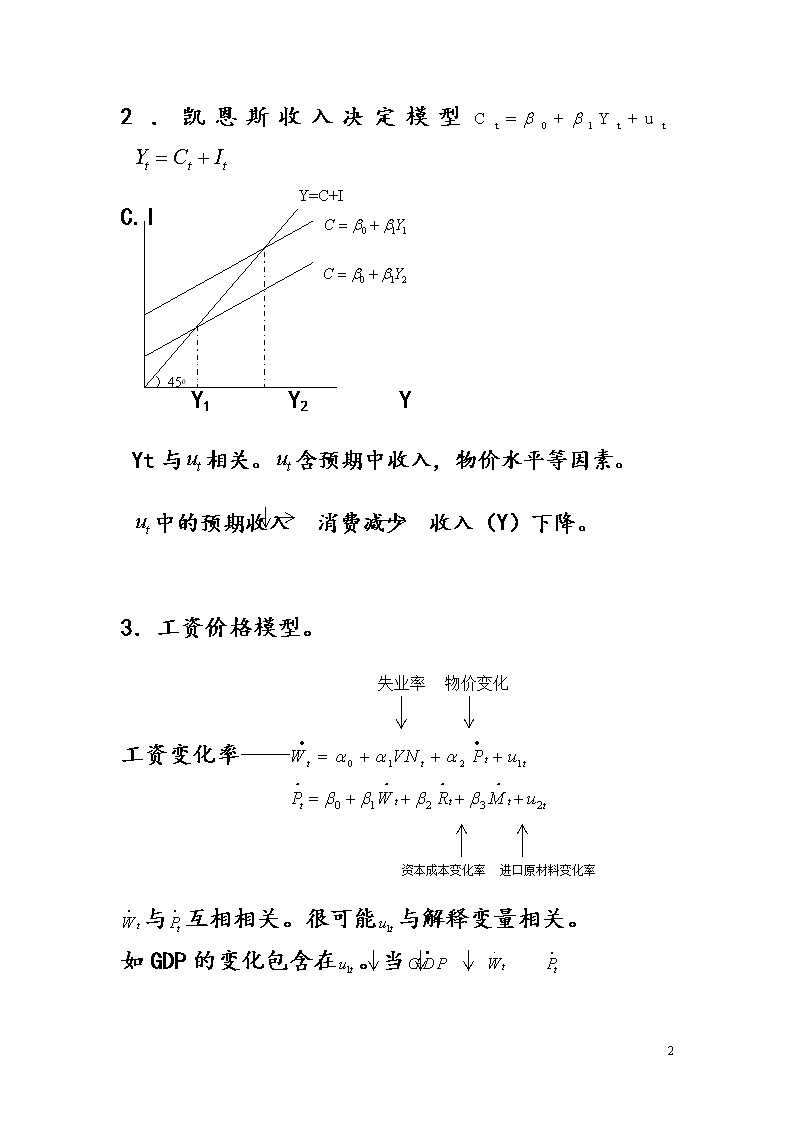
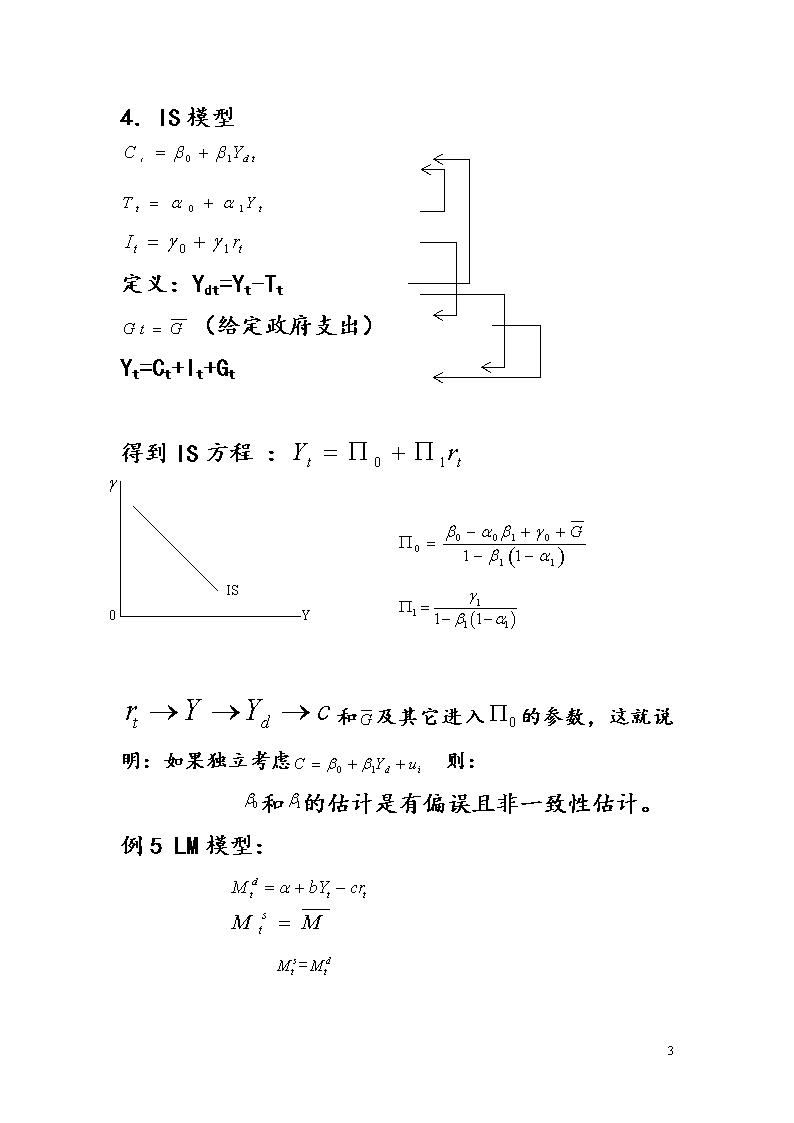
Ch18章联立方程模型在单一方程模型中,凭什么说解释变量是给定的?谁天生就是解释变量的?解释变量与扰动项之间是否有关系?一、联立方程的性质:X和Y之间有双向或联立关系。除非能说明与或与是互相独立的。二、联立方程模型的举例1.需求与供给模型:(<0)(>0)ABPOQ0D0D1S1S0DCQ均衡条件:=此模型中,与是相关的,与是相关的。(收入,财富)QP22\n2.凯恩斯收入决定模型Y=C+I)450C.IY1Y2YYt与相关。含预期中收入,物价水平等因素。中的预期收入消费减少收入(Y)下降。3.工资价格模型。失业率物价变化资本成本变化率进口原材料变化率工资变化率——与互相相关。很可能与解释变量相关。如GDP的变化包含在。当22\n4.IS模型定义:Ydt=Yt-Tt(给定政府支出)Yt=Ct+It+Gt得到IS方程:YIS0和及其它进入的参数,这就说明:如果独立考虑则:和的估计是有偏误且非一致性估计。例5LM模型:=22\n得到LM方程:YLM0(其中:)三.联立方程偏误:OLS估计量的非一致性设:,22\n一个数值性的例子(P686)给定:,根据可以生成,再来验证无偏性。四、结构模型设:22\n其中:Y1t、Y2t……YMt为M个内生变量(endogenous)X1t、X2t……Xkt为k个前定变量:外生或滞后内生上述模型为结构模型。、为结构参数从结构方程组可以解出M个内生变量并导出诱导型方程和相应的诱导型系数。(诱导型方程是指由前定变量或随机干扰来表达一个内生变量的方程。)例如:0<<1结构模型内生变量:、外生变量:推出如下诱导型模型:22\n由于与或不相关。因此可用OLS估计诱导模型系数,从诱导型系数反计算出结构系数。这种方法称为间接最小二乘法。——ILS(indirectleastspuares)五、识别问题识别问题,是指能否从诱导型方程函数求出结构方程参数的估计值。如果能,则说该方程是可以识别的。如果不能,则说该方程是不可识别的或不足识别的。1.不足识别如:在供求模型中,因诱导型只有2个系数,而结构模型有4个系数,很难从诱导型系数得到结构系数的唯一值。22\n另一种方法:用(01)去乘一个方程,同时用(1-)去乘另一个方程,得到如下:(1-)两方程相加得这个伪造的方程(线性组合)与前两个方程没有结构上的区别。因此无法知道是在估计哪一方程。2恰好识别考虑如下模型(需求与供给)22\n,,,从4个诱导系数难以估计5个结构系数。但可以看出:因此,从诱导型可以估计出供给函数,所以,供给方程是可识别的,而需求方程是不足识别的。同样也可以用伪造法判定:需求模型是不可识别的。用乘以需求方程,(1-)乘以供给方程,加起来得到混杂方程。可见混杂方程与需求方程没有结构性区别。考虑如下方程:有6个诱导系数,正如有6个结构系数,一般可求得唯一解。因此结构模型都是可识别的。同样可用“混合”模型办法予以解决。22\n3.过渡识别考虑如下模型:Q:需求或供给量,,价格。:收入,:财富。此模型的内生变量:,此模型的前定变量:,,诱导方程可估计出8个诱导系数。结构方程只有7个结构系数,由8个方程求7个未知数,得出现一个变量多个解。因此难以求出7个结构系数的唯一值。如:为什么前面例中,供给函数是可识别的,而后面是不可识别的。问题出在过多信息,当然过多信息不定是一件坏事。22\n六.识别规则设:M=模型中内生变量的个数。m=给定方程中内生变量的个数。K=模型中前定变量的个数。k=给定方程中前定变量的个数。1.可识别性的阶条件(即一个必要而非充分条件)a.定义:在一个含有M个联立方程的模型中,为了使一个方程能被识别,就必须排除M-1个在模型中的变量,如果它恰好排除了M-1个变量,则该方程是恰好识别的,它排除多于M-1个变量,则它是过度识别的。b.定义:在一个含有M个联立方程的模型中,为了使一个方程能被识别,该方程能排除的前定变量的个数必须不少于它能含有的内在变量的个数减1,即。如果,则方程是恰好识别的,如果,则它是过度识别的。以上两个定义是等价的(∵)例见:,例19.1,和19.2,19.3,19.422\n1.可识别的秩条件定义:在一个含M个内生变量的M个方程的模型中,一个方程是可识别的,当且仅当,我们能从模型(其它方程)所含而该方程所不含的诸变量(内生或前定)的系数矩阵中构造出至少一个(M-1)×(M-1)阶非零行列式。如:本模型排除了的变量:从阶条件看,上述模型都是可识别的。从秩条件看,1方程编号-1--04-00(1)-0+1-0--0(2)--0+10--0(3)-0-0100-(4)22\n方程(1),本方程没有而其它方程含有的变量的系数矩阵:该矩阵的秩为2,因此没有一个不为0的三阶行列式方程(2):秩条件的应用步骤:1)象上表一样把方程组写成表格形式。2)划掉被考虑方程所在行的系数。3)划掉被考虑方程所在行不为零的系数。4)从剩下的系数构成的矩阵,如果矩阵中含有一个M-1阶行列式,则方程是可识别的,如果找不到,则方程是不可识别的。22\n阶条件和秩条件的相结合,得到如下结论:a)如果K-k>m-1且A矩阵的秩是M-1,则方程是过度识别的。b)如果K-k=m-1且A矩阵的秩是M-1,则方程是恰好识别的。c)如果K-k≥m-1且A矩阵的秩是