[经济学]微观经济学习题答案 36页

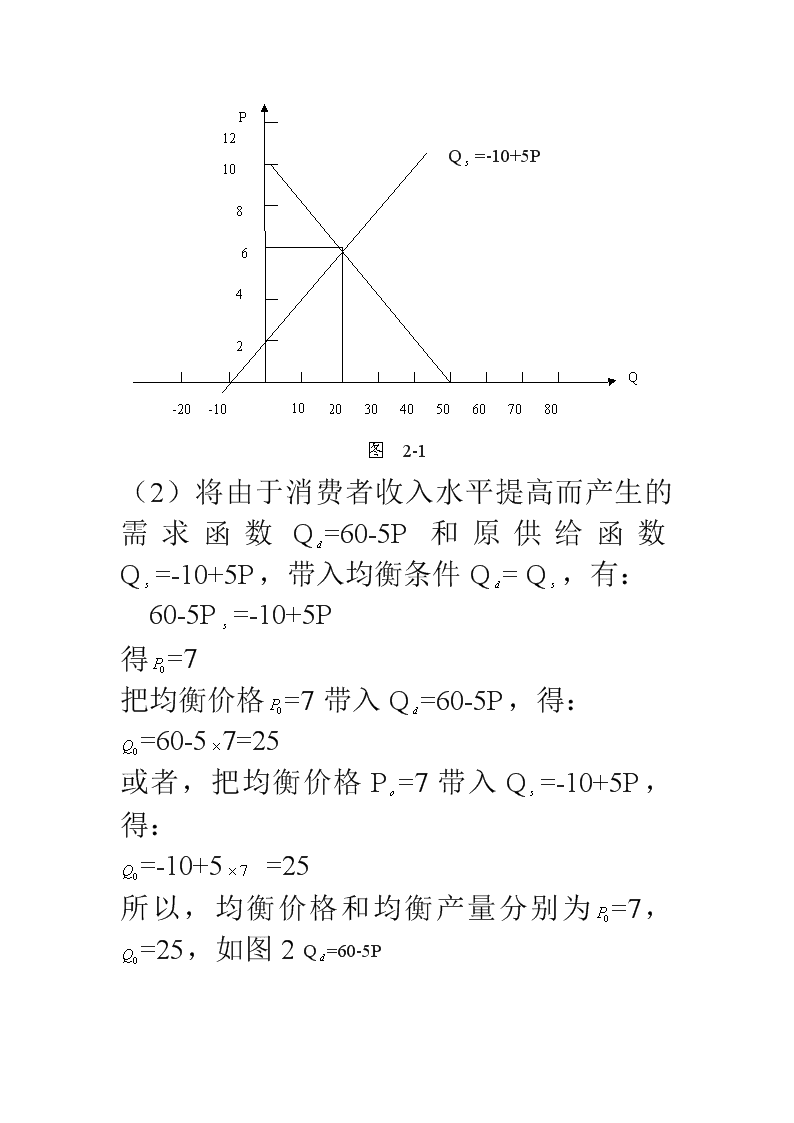
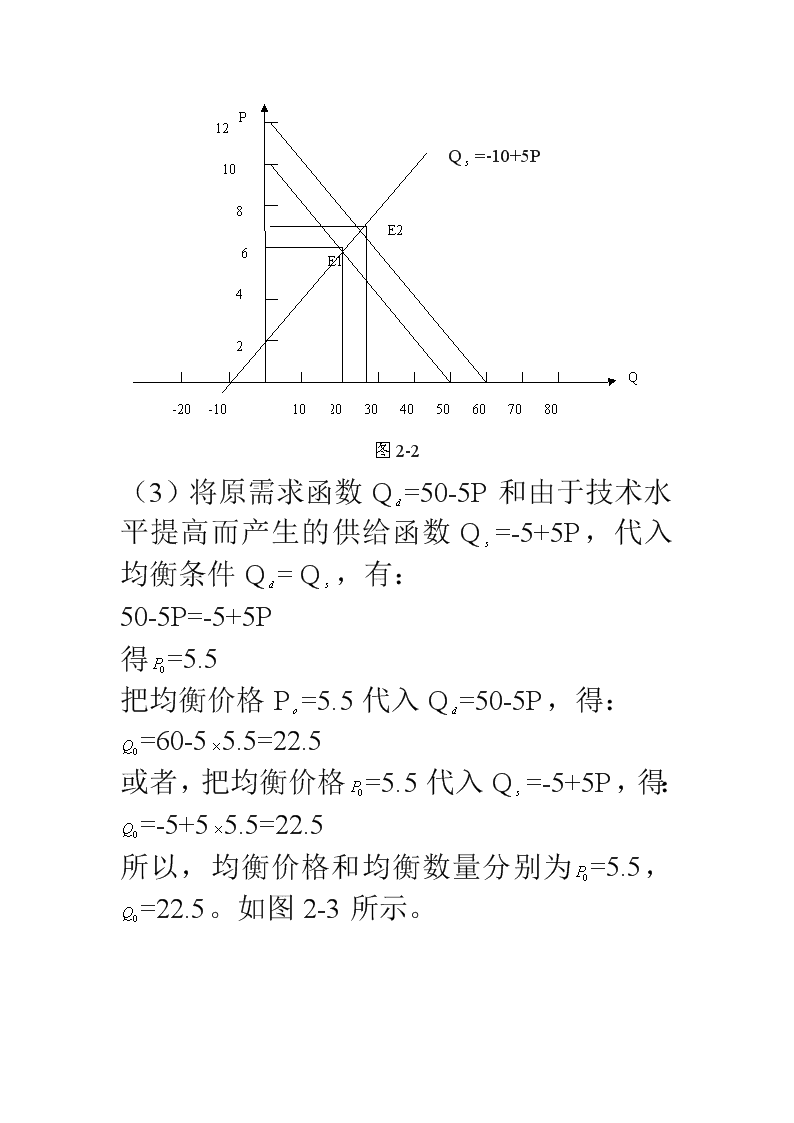
微观经济学习题答案第二章需求、供给与均衡价格1、2、3、4、5、6、7（略）8.解：（1）将需求函数Q=50-5P和供给函数Q=-10+5P带入均衡条件Q=Q，有50-5P=-10+5P得=6把均衡价格=6带入需求函数Q=50-5P，得：=50-56=20或者，把均衡价格P=6带入供给函数Q=-10+5P，得：=-10+56=20所以，均衡价格和均衡数量分别为=6，=20。如图2-1所示\n1024610812P-20-1020304050607080QQ=-10+5P图2-1（2）将由于消费者收入水平提高而产生的需求函数Q=60-5P和原供给函数Q=-10+5P，带入均衡条件Q=Q，有：60-5P=-10+5P得=7把均衡价格=7带入Q=60-5P，得：=60-57=25或者，把均衡价格P=7带入Q=-10+5P，得：=-10+5=25所以，均衡价格和均衡产量分别为=7，=25，如图2-2所示Q=60-5P\nE21E1124610812P-20-1020304050607080QQ=-10+5P10图2-2（3）将原需求函数Q=50-5P和由于技术水平提高而产生的供给函数Q=-5+5P，代入均衡条件Q=Q，有：50-5P=-5+5P得=5.5把均衡价格P=5.5代入Q=50-5P，得：=60-55.5=22.5或者，把均衡价格=5.5代入Q=-5+5P，得：=-5+55.5=22.5所以，均衡价格和均衡数量分别为=5.5，=22.5。如图2-3所示。\n24610812P-20-1020304050607080QQ=-10+5PQ=-5+5PE11E21（4）由（1）和（2）可见，当消费者收入水平提高导致需求增加，即表现为需求曲线右移时，均衡价格提高了，均衡数量增加了。由（1）和（3）可见，当技术水平提高导致供给增加，即表现为供给曲线右移时，均衡价格下降了，均衡数量增加了。总之，一般地有，需求与均衡价格成同方向变动，与均衡数量成同方向变动；供给与均衡价格成反方向变动，与均衡数量成同方向变动。第三章弹性1、2、3、4、5、6、（略）7解：（1）根据中点公式e=-有：e=-=1.5\n（2）由于当P=2时，Q=500-100=300，所以，有：e=（3）根据图3-1，在a点即P=2时的需求的价格点弹性为：e==或者e=OaAB54321100200300400500600QP图3-1显然，在此利用几何方法求出的P=2时的价格点弹性系数和（2）中根据定义公式求出的结果是相同的。都是e=8.解：（1）根据中点公式e=,有：e=（2）由于当P=3时，Q=-2+23=4，所以，e==2\n（3）根据图3-2，在a点，即P=3时的供给价格点弹性为：e=Q=2-2P-2-1123454321图3-2显然，在此利用几何方法求出的P=3时的供给价格弹性系数和（2）中根据定义公式求出的结果是相同的，都是e=1.5。9解：由已知条件M=100Q，可得Q=于是，有：进一步，可得e=/=观察并分析以上计算过程及其结果，可以发现，当收入函数M=aQ\n（其中a>0为常数）时，则无论收入M为多少，相应的需求的收入点弹性恒等于。10．解：（1）关于A厂商：由于P=200-Q=200-50=150,且A厂商的需求函数可以写成：Q=200-P于是，A厂商的需求的价格弹性为：e=-=-(-1)=3关于B厂商：由于P=300-0.5Q=300-0.5，且B厂商的需求函数可以写成：Q=600-2P于是，B厂商的需求的价格弹性为：e=-(2)令B厂商降价前后的价格分别为P和P，且A厂商相应的需求量分别为Q和Q，根据题意有：P=300-0.5Q=300-0.5P=300-0.5Q=300-0.5Q=50Q=40\n因此，A厂商的需求的交叉价格弹性为：e=(3)有（1）可知，B厂商在P=250时的需求的价格弹性为e=5，也就是说，对B厂商的需求是富有弹性的。我们知道，对于富有弹性的商品而言，厂商的价格和销售收入成反方向的变化，所以，B厂商将商品价格由P=250下降为P=220，将会增加其销售收入。具体的有：降价前：，当P=250且Q=100时，B厂商的销售收入为：TR=PQ=250100=25000降价后，当P=220且Q=160时，B厂商的销售收入为：TR=PQ=220160=35200显然，TR0所以，当Q=10时，LAC曲线达最小值。以Q=10代入LAC函数，可得：最小的长期平均成本=10\n综合（1）（2）的计算结果，我们可以判断（1）中的行业未实现长期均衡，因为，由（2）可知，当该行业实现长期均衡时，市场的均衡价格应等于单个厂商LAC曲线最低点的高度，即应该有长期均衡价格P=100，且单个厂商的长期均衡产量应该是Q=10，且还应该改有每个厂商的利润=0.而事实上，由(1)可知，该厂商实现利润最大化时的价格产量和利润都大于行业长期均衡时对单个厂商的需求。因此，（1）中的行业未处于长期均衡状态。（3）由（2）可知，当该行业处于长期均衡时，单个厂商的产量Q=10，价格等于最低的长期平均成本。即有P=100，利润=0.（4）由以上分析可以判断：（1）中的厂商处于规模不经济阶段，其理由在于：（1）中单个厂商的产量Q=20，价格P=600，它们都分别大于行业的长期均衡时单个厂商在LAC曲线最低点生产的产量Q=10和面对的价格P=100.换言之，（1）中的单个厂商利润最大化的产量和价格组合发生在LAC曲线最低点的右边，即LAC曲线处于上升段，所以，单个厂商处于规模不经济阶段。10.（1）根据题意有：LMC==-24Q+40且完全竞争的厂商P=MR，根据已知条件P=100，故有MR=100.由利润最大化的原则MR=LMC，得：-24Q+40=100解得Q=10\n又因为平均成本函数LAC(Q)==-12Q+40所以，以Q=10代入上式，得：平均成本值SAC=10最后，利润=TR-STC=PQ-STC=(10010)-(10)=800因此，当市场价格P=100时，厂商实现MR=LMC时的产量，Q=10，平均成本SAC=20利润为800。（2）由已知的LTC函数，可得：LAC(Q)=Q-12Q+40令=0,即有：=2Q-12=0解得Q=6且=2>0故Q=6是长期均衡成本最小化的解以Q=6代入LAC(Q)，得平均成的最小值为：LAC=6-126+40=4由于完全竞争行业长期均衡时的价格等于厂商的最小长期平均成本，所以，该行业长期均衡时的价格P=4单个厂商的产量Q=6\n（3）由于完全竞争市场的成本不变，行业的长期供给曲线是一条水平线，且相应的市场长期均衡价格是固定的，它等于单个厂商的最低的长期平均成本，所以，本题的市场均衡价格固定为P=4.以P=4代入市场需求函数，Q=660-15P，便可以得到市场的长期均衡数量为Q=660-154=600。现已求得在市场实现长期均衡时，市场的均衡数量Q=600，单个厂商的均衡数量为6，于是，行业长期均衡时的厂商数量=6006=100（家）。11．解：（1）在完全竞争市场均衡时有LS=D，即有：5500+300P=8000-200P，解得P=5以P=5代入LS函数或者D函数，得Q=5500+3005=7000所以，市场的长期均衡价格和均衡数量分别为P=5，Q=7000（2）同理，根据LS=D，有，5500+300P=10000-200P解得P=9把P=9代入D函数或LS函数，得Q=5500+3009=8200所以市场扫尾长期均衡函数价格和均衡数量分别为P=9，Q=8200（3）比较（1）和（2）得，对于完全竞争成本递增行业而言，市场需求增加，会使市场的均衡价格上升，使市场的均衡数量也增加。12.解：（1）根据市场短期均衡的条件D=SS,有6300-400P=3000+150P解得P=6以P=6代入市场需求函数或市场短期供给函数有：\nQ=6300-4006=3900所以，该市场短期均衡价格和均衡产量分别为P=6Q=3900（2）因为该市场短期均衡时的价格为P=6，且由题意可知，单个企业在LAC曲线最低点的价格也为6，所以，由此可以判断该市场同时处于长期均衡。因为由（1）可知，市场长期均衡时的数量是Q=3900，是有题意可知，在市场长期均衡时单个企业的产量为50，由此，可以求出市场长期均衡时的厂商数量为：390050=78（家）（4）与（2）中的分析相类似，在市场需求函数和短期生产函数变化之后，该市场短期均衡时的价格P=6，由题意可知，单个企业在LAC曲线最低点的价格也是6，所以，由此可以判断该市场的短期均衡同时又是长期均衡。因为由（3）可知，供应函数变化后的市场长期均衡时的产量Q=5600，且由题意可知，在市场长期均衡时单个企业的产量为50，所以，可以得出市场长期均衡时的行业内的厂商数量：560050=112（家）（5）由以上分析和计算过程可知：在市场供求函数发生变化前后的市场长期均衡时的均衡价格是不变的，均为P=6，而且，单个企业在LAC曲线最低点的价格也是6，于是，我们可以判断该行业属于成本不变行业。（6）\n由（1）（2可知，（1）时的厂商数量为78家；由（3）、（4）可知，（3）时的厂商数量为112家。因为，由（1）到（3所增加的厂商数量为：112-78=34（家）第四章不完全竞争市场1、2、3、4、5、6（略）7.答：三级价格歧视要求厂商在需求价格弹性小的市场上制定较高的产品价格，在需求弹性大的市场上制定较低的产品价格，以获得比制定统一价格更高的利润。在本题中，由于学生的需求弹性较大，而普通旅客的需求弹性较小，因此，学生票价应定的低于普通旅客票价，以此获取更高的利润。8.解：（1）由已知条件可得收益函数为：TR=P(Q)Q=（8-0.4Q）Q=8Q-0.4Q令=0，即有：=8-0.8Q=0解得：Q=10=-0.8<0，所以，当Q=10时，TR值达最大值。以Q=10代入反需求函数，P=8-0.4Q，得P=8-0.410=4以P=4，Q=10代入利润等式，有：=TR-TC=PQ-TC=（410）-（0.610+310+2）=-52所以，当该垄断厂商实现收益最大化时，其产量Q=10，价格P=4，收益TR=40,利润=-52，即该厂商的亏损为52.\n（2）由题意可得：MC==1.2Q+3且因为P=8-0.4Q，所以MR=8-0.8Q于是，根据利润最大化的原则MR=MC有：8-0.8Q=1.2Q+3解得：Q=2.5以Q=2.5代入反需求函数P=8-0.4Q，得：P=8-0.42.5=7以Q=2.5P=7代入利润等式，有：=TR-TC=PQ-TC=（72.5）-（0.62.5+32.5+2）=4.25所以，该厂商实现利润最大化时，其产量Q=2.5，价格P=7，收益TR=17.5，利润=4.25（3）通过比较（1）和（2）可知；将该垄断厂商实现利润最大化的结果与现实收益最大化的结果相比较，该厂商实现利润最大化时的产量较低（2.5<10），价格较高（7>4），收益较少（17.5<40），利润较大（4.35>-52）。显然，理性的垄断厂商总是以利润最大化为生产目标，而不是将利益最大化作为生产目标。追求利润最大化的垄断厂商总是以较高的垄断价格和较低的产量，来获得最大的利润。\n9.解：（1）由第一个市场的需求函数Q=12-0.1P可知，该市场的反需求函数为P=120-10Q，边际收益函数为MR=120-20Q.同理，由第二个市场需求函数Q=20-0.4P可知，该市场的反需求函数P=50-2.5Q.边际收益函数为MR2=50-5Q2此外，厂商生产的边际成本函数MC==2Q+40该厂商实行三级价格歧视时利润最大化的原则可以写成：MR=MR=MC于是关于第一个市场：根据MR=MC，有：120-20Q=2Q+40即22Q+2Q=80①关于第二个市场：根据MR=MC，有：50-5Q=2Q+40即2Q+7Q=10②由①②两式解得，厂商在两个市场的销售量分别为：Q=3.6Q=0.4将各自产量代入各自反需求函数，可得两个市场的价格分别为P=84\nP=49在实行三级价格歧视时厂商的总利润为：=（TR+TR）-TC=PQ+PQ-(Q+Q)-40(Q+Q)=146(2)当该厂商在两个市场上实行统一的价格时，市场需求函数Q=Q+Q=(12-0.1P)+(20-0.4P)=32-0.5P而且，市场反需求函数为P=64-2Q市场的边际收益函数为:MR=64-4Q根据利润最大化的原则，即该统一市场的MR=MC有：64-4Q=2Q+40解得Q=4以Q=4代入市场反需求函数P=64-2Q得P=56于是厂商的利润为：=PQ-TC=（564）-（4+404）=48所以，当该垄断厂商在两个市场上实行统一价格时，他追求利润最大化的销售量为Q=4，价格为P=56，总的利润为=48.\n（3）比较（1）（2）的结果，可以清楚的看到，该垄断厂商实行三级价格歧视和在两个市场实行统一定价的两种做法相比较，在两个市场制定不同的价格来实行三级价格歧视时所获得利润大于在两个市场实行统一定价时所获得的利润（因为146>48）。这一结果表明，进行三级价格歧视比统一价格更为有利可图。第四章博弈论初步1、2、3、4、5、6（略）7、解：（1）这两个厂商没有占优战略均衡。因为无论对厂商A还是厂商B而言，他们的最优战略都不是唯一的，而取决于对方的战略选择。（2）该博弈有纳什均衡。有两个。他们是战略组合：（高档、中档）和（中档、高档），各自对应的支付为：（80，100）和（100，80）（3）高档中档高档中档高档（50，50）（100，80）（80，100）（40，40）B中档B\nA8.解：（1）这是一个“囚犯的困境”。因为该博弈有一个占优战略均衡：（做广告，做广告），而显然，这是一个对双方都不利的结果。它反映了个体理性与集体理性的冲突。（2）如果该对局只进行一次。其纳什均衡是：（做广告，做广告），该纳什均衡也是一个占优战略均衡。（3）厂商B在第一次做广告的情况下的累计利润为：300+100+100+100+100+100+100+100+100+100=1200厂商B在第一次不做广告的情况下的累计利润为：200+100+100+100+100+100+100+100+100+100=1100所以厂商将做广告。说明在有限期重复博弈中，博弈的均衡是（不合作，不合作）即（做广告，做广告）。9．解：（1）厂商A(3)1厂商B(1)厂商A(2)21（100，4）2（70，50）1（80，90）2（60，80）（2）\n对于厂商B来说。当然选择则所有结局中最有利于自己的。但它将首先考虑厂商A在两种情况下的选择。厂商B可以判断，在结点（2），厂商A在比较两种结局之后选择2的策略；在结点（3），厂商A会选择1的策略。然后，厂商B在这种结局，即（1，2）和（2，1）中选择，显然后者对厂商A最有利，此时，厂商A获利90。厂商B获利80，所以，如果B先行，此序列博弈的纳什均衡点是（2，1）10.解：（1）这一威胁不可信。因为该博弈的结局是（进入，接纳），这是一个纳什均衡。（2）该卡特尔组织可扩大生产规模，通过投资来形成一部分剩余的生产能力。这一部分生产能力在没有竞争者进入市场时是多余的，只是在进入发生时投入作用，使其成为抵制进入者的有利武器。并向外宣称：新扩大的生产规模目前是闲置的，在位者愿意花费相当的资金来维护闲置的生产设备。但是，只要潜在进入者敢于进入此行业，在位者则立即运用那部分扩大的闲置的生产能力来进行生产。并将大量的产品抛向市场。以压低市场价格，在被压低的市场价格下，实力雄厚的在位者能够承受这样的价格压力，所以，潜在进入者便可能放弃进入该行业，在位者的威胁策略便可能成功。第四章生产要素的需求与供给1、2、3、4、5（略）6.解：根据生产函数及产品价格P=0.\n10，可求出劳动的边际产品价值如下（其中MPP表示劳动的边际产品）VMP=PMPP=P=0.10(-0.10L+L+38L)’=0.10(-0.03L+2L+38)完全竞争厂商的利润最大化要求边际产品价值等于工资，即：5=0.10(-0.03L+2L+38)解得：L=L=60当L=时，利润最小（因为=1.6>0）,故略去。当L=60时，利润最大（因为=-1.6<0）,故厂商每天要雇佣60小时的劳动。7.解：卖方垄断市场的要素使用原则为：MRP=MFP=W而MRP=MPMR由题目已知条件P=600-Q可得MR=600-2QMP==所以，=50，解得L=7该厂雇佣7个工人8.解：由q=6L+3L-0.02L得MPP==6+6L-0.06L于是VMP=PMPP=12+12L-0.12L由C=WL=60L+3L，得MFC==60+6L根据VMP=MFC，有12+12L-0.12L=60+6L解得L=40\n于是当利润最大化时有L=40由q=640+340-0.0240=3760W=60+340=1809.解：由Q=100-P即P=100-Q及Q=4L得：TR=PQ=(100-Q)Q=(400-4L)4L=400L-16LMRP==400-32L由L=0.5w-20即w=2(L+20)得：TC=Wl=2（L+20）L=20L+40LMFC==4L+40利润最大化要求MRP=MFC，即400-32L=4L+40于是L=10Q=4L=410=40W=2(20+L)=2(20+10)=60P=100-Q=100-40=6010.解：由P=100-Q以及Q=2L得：TR=PQ=(100-Q)Q=(100-2L)2L=200L-2LMRP==200-8L由L=-40+w即w=L+40得：TC=Wl=（L+40）L=L+40LMFC==2L+40（1）完全竞争产品市场和要素市场中的完全竞争厂商使用要素的原则为：VMP=W，即MPP=w\nMP==2所以，2（100-Q）=L+40，把Q=2L代入解得：L=32W=L+40=32+40=72（1）卖方垄断厂商的要素使用原则为：MRP=MFC=W所以200-8L=L+40，解得：L=18W=L+40=18+40=58第四章生产要素的价格决定1、2、3、4、5、6（略）7.解：（1）均衡时，D=S，即4000-50w=50w，由此得均衡工资w=40。（2）如果政府对工人提供的每单位劳动课以10美元的税收，则劳动供给曲线变为：S’=50(w-10)由S’=D，即50(w-10)=4000-50w，解得。W=45即征税后的均衡工资为45（2）征税后，厂商购每单位劳动要支付的工资变为45美元，而不是征税前的40美元。两者之间的差额5美元即是厂商为每单位劳动支付的税收额。工人提供每单位劳动得到45美元，但是有10美元要作为税收交给政府。所以，仅能留下35美元。工人实际得到的单位工资与征税前相比也少了5美元，这5美元就是他们提供单位劳动而实际\n支付的税款。因此，在此例中，厂商和工人恰好平均承担了政府征收的10美元的税款。（1）征税后的均衡劳动雇佣量为：50（w-10）=50(45-10)=1750政府征收到的税收总额为：101750=17500