《统计学》课件 21页

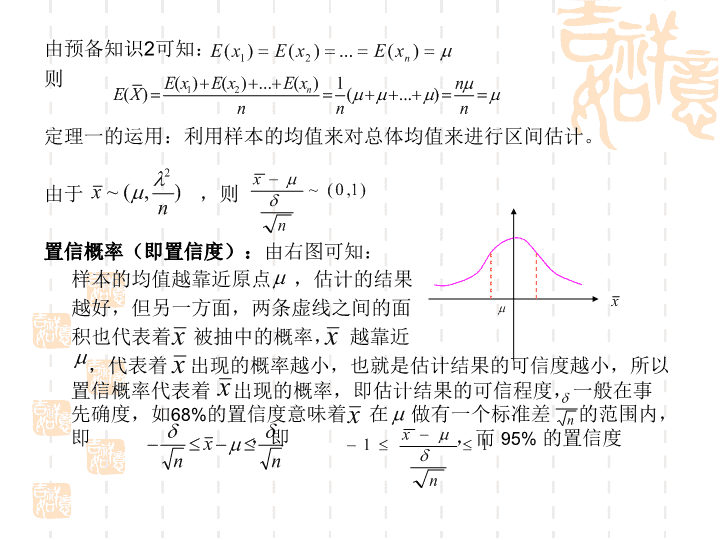
参数估计预备知识：1.随机抽样的定义。设总体由N个数X1，X2…Xn构成，它的均值：方差：现从总体中进行若干次（假设为N次）有放回的重复抽样，每次抽样的结果记为x1，x2…xn，则x1，x2…xn为n个独立随机变量。\n2.随机抽样的分布。每次随机抽样的结果都是一个独立随机变量，其概率分布如下（设随机变量x为一次随机抽样的结果）：则随机变量X的数学期望为：随机变量的方差为：一、定理一：随机抽样的均值，即，只证明。对于n次独立随机抽样，其均值则Xx1x2…xnP1/N1/N…1/N\n由预备知识2可知：则定理一的运用：利用样本的均值来对总体均值来进行区间估计。由于，则置信概率（即置信度）：由右图可知：样本的均值越靠近原点，估计的结果越好，但另一方面，两条虚线之间的面积也代表着被抽中的概率，越靠近，代表着出现的概率越小，也就是估计结果的可信度越小，所以置信概率代表着出现的概率，即估计结果的可信程度，一般在事先确度，如68%的置信度意味着在做有一个标准差的范围内，即，即，而95%的置信度\n意味着落在左右1.96个单位标准差的范围内，即由于，n,均属已知，故只要给定置信概率，就可以利用上面的不等式求出的区间估计。二、定理二：随机样本方差的数学期望。证明：设总体的均值为，方差为，从中随机抽取容量为n的样本x1，x2…xn，则，x1，x2…xn以及都是随即变量。样本方差……①则\n对于则由预备知识2可知：另由于\n则令……②则故比是得更好的估计。从①与②式可知：卡方分布定义：如果随机变量X1，X2…Xn均服从标准正态分布，则随机变量服从自由度为n的卡方分布。三、定理三：服从自由度为n-1的卡方分布。证明：由前面定理二可知：\n则由于X1，X2…Xn均为来自于总体的独立随机变量，也就是，…则，…由于，则，则根据卡方分布定义：服从自由度为n-1的卡方分布。\n定理三的应用：利用样本方差来估计总体方差。由定理三可知：服从自由度为n-1的卡方分布和总体均值的估计方法一样，依靠给定的概率置信度，我们可以确定落在与之间，即，由于，，n,为已知，我们可以通过解不等式而得到的区间估计。四、在总体方差未知时，如何利用样本均值来估计总体均值？定义T分布。如果随机变量Y服从标准正态分布，随机变量z服从自由度为n的卡方分布，则：随机变量服从自由度为n的T分布。定理四：服从自由度为n-1的T分布。证明：从前面已知，则令，\n则根据T分布定义：服从自由度为n-1的T分布。或定理四的应用：在总体方差未知时，利用样本均值来估计总体均值。由定理四可知：或服从自由度为n-1的T分布。我们依靠给定的置信度确定落在与之间，即由于，，s，n，为已知，故可以通过解不等式得到的区间估计。\n五、总体比例的区间估计：利用样本比例来估计总体比例总体有互斥事件A与B构成，A与B发生概率分别为p，1-p,现从总体中重复地取n个样本，在n个样本中，事件A发生的数量为x（x为随机变量），则在样本中事件A发生的比例为，要求利用样本的比例对总体比例p进行区间估计。首先，求样本比例的分布：E()=由于x服从二项分布，则E(x)=np，=npq则：E()===p===当n足够大时x由二项分布转化成正态分布，其均值和方差分别为：(p，)。则根据给定置信概率，我们知道样本比例落入与之间的概率，即的概率。\n由于q=1-p,另有n足够大的情况下，为了方便起见，在计算方差时，用与分别代入计算，这样就可以根据上面的不等式对p进行区间估计。六、利用两个样本均值的差与和来估计两个总体均值的差与和已知：是来自总体一的样本均值，则~(,),为总体一的方差与均值，为样本容量是来自总体二的样本均值，则~(,),为总体二的均值与方差，为样本容量\n则：则：~~则根据给定的概率置信度，知道S1＋S2落入Z1与Z2之间的概率，则根据上式可以得出区间估计，如果n1,n2足够大，在计算时可以用样本的方差来代替总体方差。\n七、如何利用给定的抽样误差来确定样本容量已知样本均值服从在利用样本均值来估计总体均值的过程中，之间的距离为△，为，△由两个因素决定：一是置信概率，二是例如在95%的置信概率水平下，如果我们事先确定△，则可以根据上式计算出n.),(~2nxlm\n假设检验一、原理假设检验的目的是利用样本信息作出有关总体的决策。它首先对总体的参数作出某种假设，然后通过样本信息来决定假设是否成立。假设检验所遵循的方法是一种演绎的方法，在总体参数服从某一假设的情况下，样本的信息应该与这一假设一致，如果样本的信息和对总体参数的假设相差太大，就会使人自然怀疑原有假设是否正确，当然样本信息和假设之间的差异有可能是由于抽样的随机性引起的，尽管这种情况的出现是一个小概率事件。但人们对小概率事件往往持否定态度，所以往往会根据小概率事件出现的结果来拒绝原假设。假设检验中，我们一般以显著性水平作为小概率的界限，所以假设检验又称为显著性检验。二、如何建立假设原假设：与备择假设对应的假设，也就是需要通过样本去推断是否正确的命题。备择假设：一般将期望出现的假设作为备择假设，备择假设无法自我直接证明，而是通过对原假设的否定而得到间接的证明。由备择假设决定进行双测和单测检验。\n三、构造统计量在确定和后，就要构造统计量来决定哪一个假设是正确的。统计量依据原假设对总体参数的设定来构造，确定统计量后，利用统计量的分布与事先确定的显著性水平，来确定对原假设的接受区域为和拒绝区域，接受区域为，是大概率区域，后者为，是小概率区域。例一：利用假设检验来检验一枚硬币是否均匀。决策如下：在投掷100次的一个样本中，如果正面出现的次数在40～60之间，则接受假设，否则拒绝假设。求：①当假设正确时，拒绝假设的概率②如果在100次投掷中产生了53次正面，60次正面，是否支持原假设③在②中你的结论是否会犯错误，请解释解：①投100次硬币出现40～60次正面的概率为P（40≤X≤60）X～（np,npq)的正态分布np＝100×＝50npq=100×=25则X～（50，25）则P（40≤X≤60）＝P（）＝P（）则所求概率为0.4772×2＝0.9544\n如果硬币是均匀的，出现正面次数不在40～60之间的概率为1－0.9544＝0.0456，所以假设正确而被拒绝的概率为0.0456②根据①的结果可以画出接受域与拒绝域，由于53和60都落在接受域里，故认为原假设是正确的。③会犯错误。当假设实际上应该被拒绝时，我们可能接受该假设。例如实际情况是正确出现的概率是0.7而不是0.5。例二、要求以0.05的显著性水平检验一枚硬币是否均匀。已知样本为连续投掷64次硬币，问如何给出接受域？解：另X代表正面出现的次数，在0.5的显著性水平下，X的标准化值分别－1.96，1.96由于X~(np,npq)np=64×＝32npq＝64×＝16所以X~(32,16)则X的标准化为则在两个临界点的X为\n得出X＝24.16和X＝39.84则在0.05的显著性水平下，如果正面出现的次数在24.16~39.84之间就可以接受原假设。四、两种类型的错误：弃真，取伪第一类错误：弃真，在原假设是正确的情况下，拒绝原假设，犯第一类错误的概率伪显著性水平的大小。第二类错误：取伪，把不正确的原假设当成正确的加以接受的错误。例三：在例一中，如果真实情况是正面出现的概率是0.7时，接受硬币是均匀的这一假设的概率是多少？解:当P＝0.7时，投掷100次正面在40～60次的概率为：P（40≤X≤60）X~（np,npq)np＝100×0.7＝70npq＝4.582则P（40≤X≤60）＝P（）＝P（）=0.0145五、涉及均值或比例的差的检验例四：两个班分别有40个和50个学生，进行一场测验，第一班分别为74，标准差为8，第二班平均分为78，标准差为7，要求在0.05的显著性水平检验两个班的成绩是否有显著差异。解：设两个班来自两个总体，均值分别为和\n则在下，两个班的均值相等，则则样本的标准化值为：在0.05的显著性水平下，临界值为±1.96。－2.49在－1.96之外，已落入已落入拒绝域故拒绝原假设。例五：有A、B两群病人，每群100人，给A群一种药，B不给，其余完全一样，结果A群分别有75人和65人痊愈，要求以0.01的显著性水平检验该药对疾病有效。解：设P1与P2分别是使用药物和不使用药物两群人重的痊愈比例在假设下，则而在0.01的显著性水平下，Z＝2.53故接受原假设六、卡方检验：检验观测值与期望值之间是不是存在显著差异统计量｛\nf为实际观测值e为期望值原理：从二项总体中抽取容量n的样本，为了确定其中成功的概率P是否与总体的成功概率显著不同，现用比例的检验或成功次数的检验，令分别代表成功和失败，样本中成功的次数为x，则失败的次数为n-xz，则X～（np,npq)P为总体成功的比例事件（成功）（失败）观测频数xn-x期望频数npnp则卡方统计量事件A1A2……AK观测频数X1X2……XK期望频数np1np2……npk\n则自由度为k-1例六：检验一个骰子是否均匀，投掷120次后的观测频数与期望频数如下：点数123456观测频数251715232416期望频数202020202020（要求X0.05的显著性水平检验骰子是否均匀）解：所以可以认为骰子是均匀的。七：利用检验分析列联表观测值f是现存的，问题是如何计算e建立假设：X与Y不相关：X与Y相关如果成立，预期频数显然不等于观测值的频数预期频数e＝预期概率×n预期概率也就是在原假设成立时，依X与Y无关则\n这样预期频数依次计算可得预期频数表：然后计算自由度df=(r-1)(c-1)=(行数－1）（列数－1）然后根据显著性水平进行检验。例七：研究不同性别（X）的学生对父母的敬重情况（Y），从一个随机样本中得到下面的列联表，要求依0.05的显著性水平检验学生性别X对父母就敬重情况Y之间的关系。解：若X与Y无关，则在成立时的预期频数的分布为：则df=(2-1)(2-1)=1故拒绝458261197合计23316271母22599126父合计女男458261197合计23316271母22599126父合计女男