统计学时间序列 162页

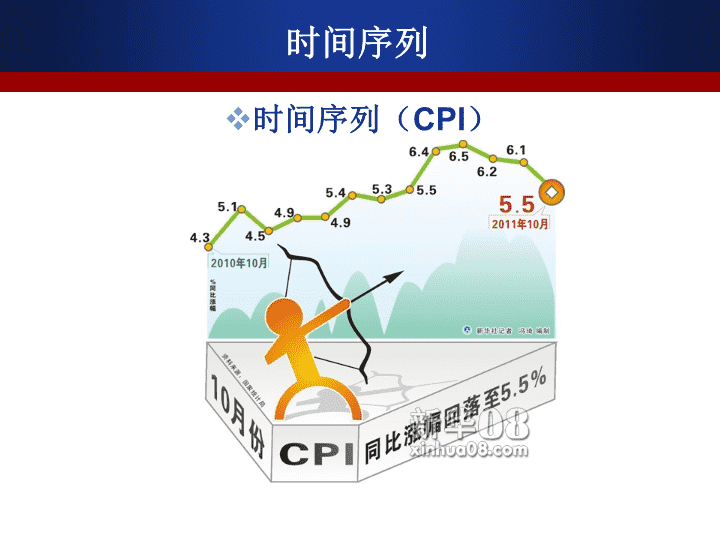
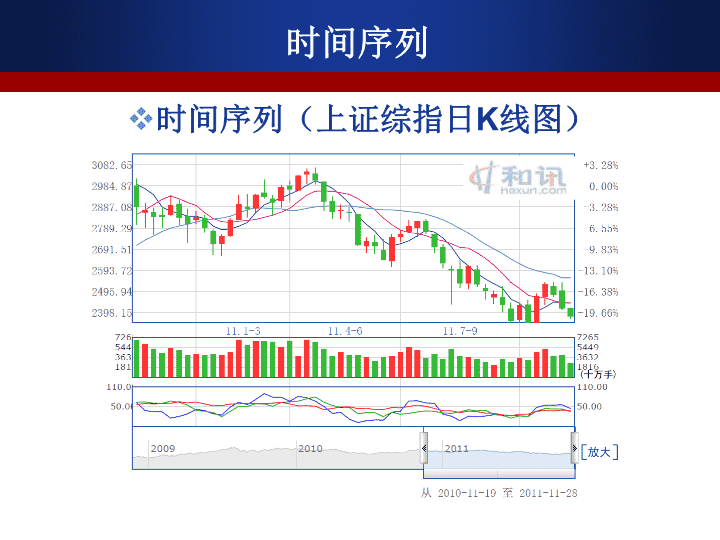
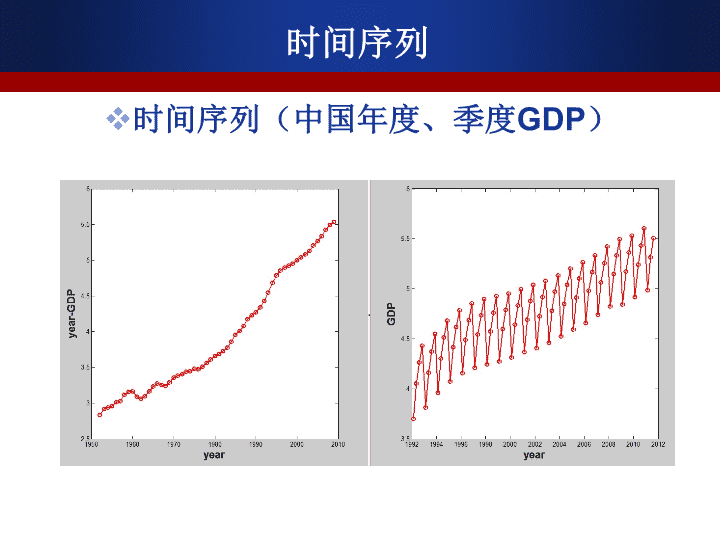
时间序列时间序列（CPI）\n时间序列时间序列（上证综指日K线图）\n时间序列时间序列（中国年度、季度GDP）\n时间序列时间序列（中国年度、季度GDP增长率）\n主要内容5.1时间序列概述5.2时间序列的水平分析5.3时间序列的速度分析5.4长期趋势变动分析5.5季节变动与循环波动分析\n学习目标掌握：时间序列的分类；时间序列的水平分析（序时平均数）和速度分析（平均发展速度与平均增长速度）；理解：长期趋势分析的方法和应用。了解：季节变动和循环波动分析的原理和应用。\n第一节时间序列的概念和分类一、概念二、分类三、编制原则\n第一节时间序列的概念和分类社会经济现象总是随着时间的推移而变化，呈现动态性。统计对事物进行动态研究的基本方法是编制时间序列。时间序列：就是把不同时间的社会经济统计指标按时间先后顺序排列所形成的数列；又称动态数列或时间数列。；描述现象发展变化的过程，是分析各种现象的动态过程及其演化规律的重要依据\n时间序列——按时间顺序排列的某项统计指标的一串数值。如：1986—2000年间，我国逐年的人均GDP，构成一个时间序列。记：y1,y2,…,yn(n项)或：y0,y1,y2,…,yn(n+1项)\n时间数列的构成要素1.现象所属的时间（时间要素）2.不同时间的具体指标数值（数据要素）。\n时间序列(一个例子)另见课本P122表5-1\n时间序列的图形描述（线图P81）\n时间序列的分类（指标的性质）总量指标（绝对数）时间序列一系列总量指标（包括单位总量和标志总量）按时间顺序排列而成；反映现象在不同时间上所达到的总规模或者总水平；时间序列中最基本的表现形式，派生出其他时间序列。\n时间序列的分类（指标的时间属性）总量质保的分类时期指标时间序列一系列时期指标按时间顺序排列而成；反映社会经济现象在一段时期发展变化的结果通常以年度、季度或者月度等时间段为单位时点指标时间序列一系列时点指标按时间顺序排列而成反映社会经济现象在某一时刻（瞬间）的情况。\n时期序列列与时点序列时期指标时间序列具有以下特点：A）可加性，不同时期的总量指标可以相加；B）指标值的大小与所属时间的长短有直接关系（正相关）。C）指标值采用连续统计的方式获得。\n时点指标时间序列具有以下特点：A）不可加性。不同时点的总量指标不可相加，这是因为把不同时点的总量指标相加后，无法解释所得数值的时间状态。B）指标数值的大小与时点间隔的长短一般没有直接关系。在时点数列中，相邻两个指标所属时间的差距为时点间隔。存在长期趋势时例外。C）指标值采用间断统计的方式获得。时期序列列与时点序列\n年份199219931994199519961997职工工资总额（亿元）3939.24916.26656.48100.09080.09405.3年末职工人数（万人）147921484914849149081484514668国有经济单位职工工资总额所占比重(％)78.4577.5577.7845.0674.8176.69职工平均货币工资（元）271133714538550062106470时间序列的种类（例）\n时间序列的分类（指标的性质）质量指标（相对指标或平均指标）时间序列一系列相对指标或平均指标按时间顺序排列而成相对指标时间序列反映社会经济现象之间相互联系的发展过程。平均指标时间序列反映社会现象发展的一般趋势\n时间序列的特点派生性—由绝对数列派生而得不可加性可加性、关联性、连续登记不可加性—不同时期资料不可加无关联性—与时间的长短无关联间断登记—资料的收集登记平均相对时期时点特点序列\n复习时点数列与时期数列P154-158：1.1，1.2，2.1，2.2\n时间序列的分类（指标的平稳性）随机性时间序列各指标值的变动除了随机因素的影响外，不存在某种规律性的变动平稳时间序列基本稳定在某个水平附件波动非平稳时间序列各指标值受各种因素的影响，存在某种规律性的变动趋势性：增加或减少的趋势季节性：随季节周期性波动\n时间序列的分类（指标的平稳性）平稳时间序列各指标值的变动除了随机因素的影响外，不存在某种规律性的变动基本稳定在某个水平附件波动平稳性数列?\n时间序列的分类（指标的平稳性）非平稳时间序列各指标值受各种因素的影响，存在某种规律性的变动。趋势性、季节性等季节性数列\n时间序列的分类（指标的平稳性）非平稳时间序列（中国年度、季度GDP）趋势性数列趋势性+季节性数列\n时间序列分类指标性质时间属性平稳性总量指标数列相对指标数列平均指标数列时期数列时点数列平稳数列非平稳数列时间序列的分类质量指标数列\n各期指标数值所属时间可比各期指标数值总体范围可比各期指标数值经济内容可比各期指标数值计算口径可比保证数列中各期指标数值的可比性编制时间序列的基本原则\n第二节时间序列的水平分析一、发展水平二、增长水平\n时间序列的水平分析时间序列的水平指标1.发展水平发展水平平均发展水平或序时（动态）平均数2.增长水平逐期增长量累计增长量平均增长量\n发展水平\n一、发展水平（一）发展水平时间序列中，各指标数值就是该指标所反映的社会经济现象在所属时间的发展水平。动态比较时：基期水平y0、报告期水平y1。\n（二）平均发展水平又叫序时平均数，动态平均数序时平均数将指标在各时间上表现的差异加以抽象，以一个数值来代表现象在这一段时间上的一般发展水平。是将时间数列中各时期的发展水平加以平均而得出的平均数。单位时间内的水平或速度解决对比性问题（如日平均产量优于月总产量）二、平均发展水平\n相同点：忽略差异，反映一般水平区别：平均对象不同：平均发展水平：时间序列动态平均一般平均数：变量数列静态平均抽象的差异不同：平均发展水平：同一现象的时间差异一般平均数：不同单位的标志值差异平均发展水平与一般平均数\n平均发展水平的计算序时平均数，要根据不同数列总量指标数列（具体又分为时期数、时点数）、相对指标数列和平均指标采用不同的计算公式计算！相对指标和平均指标由总量指标派生，总量指标时间序列的序时平均数最基本\n1.总量指标时期数列的序时平均数：算术平均法y1y2yiyn12……i……n…时期发展水平\n年份199119921993199419951996国内生产总值（亿元）2161826638346344675658478678851991～1996年平均国内生产总值：时期数列1.总量指标时期数列的序时平均数：算术平均法\n2.时点数列的序时平均数序时平均数：不同时间的指标的平均数。时点指标：描述任意时刻的状态的指标。时点指标序时平均数：所有时点上指标的平均数原则上时点无穷多，平均用积分\n2.时点数列的序时平均数实际上两种处理方式：对时间进行分割（比如最小到天），已知每个最小时点的数值（实际上是一段时间的代表值），则简单算术平均。【连续时点数列1】\n2.时点数列的序时平均数实际上两种处理方式：只记录一些时点的指标。又分两种情况1）、变动一次登记一次，则实际上所有时点的指标都已知【连续时点数列2】。\n2.时点数列的序时平均数2）、中间有变动但没有登记，则两个时点之间的指标都未知【间断时点数列】。用两个时点指标的平均值近似看成这段时期的代表值。如果间隔相等，等化简为首尾折半法\n2.时点数列的序时平均数时点序列序时平均数：所有（原则上无穷多）时点上指标的平均数。实际上只有有限个时点的数据，这些已知数据的时点将时间分割成一系列时期。时点序列序时平均数等于每个时期的代表值用时期长度作为权重的加权算术平均。\n2.时点数列的序时平均数\n年份199119921993199419951996年底人数（亿人）11.5811.7111.8511.9912.1112.241992年～1996年我国平均人口总数：【课堂练习】1991年底～1996年底我国人口总数：2.时点数列的序时平均数\n时间3月末4月末5月末6月末库存量（百件）66726468【课堂练习】某商业企业2004年第二季度某商品库存资料如下，求第二季度的月平均库存额。2.时点数列的序时平均数【分析】库存量一般变动都会登记，但不会总是在月末变动，因此是中间数据未知且等间隔，首尾折半法【对比课本P127式5-3】\n22323间隔年数1837516851140711182899498350年底人数（万人）199519971993199019881985年份【课堂练习】1985～1997年我国第三产业从业人数（年底数）我国第三产业平均从业人数：2.时点数列的序时平均数\n时间1月1日5月31日8月31日12月31日社会劳动者人数（万人）362390416420某地区1999年社会劳动者人数资料如下：【课堂练习】解：则该地区该年的月平均人数为：2.时点数列的序时平均数：\n二）.相对数数列(平均数数列）序时平均数\n⑴a、b均为时期数列时⑵a、b均为时点数列时二）.相对数数列(平均数数列）序时平均数\n⑶a为时期数列、b为时点数列时二）.相对数数列(平均数数列）序时平均数\n月份一二三计划利润（万元）200300400利润计划完成程度（﹪）125120150【例】某化工厂某年一季度利润计划完成情况如下：因为所以，该厂一季度的计划平均完成程度为：二）.相对数数列(平均数数列）序时平均数\n月份三四五六七工业增加值（万元）11.012.614.616.318.0月末全员人数（人）20002000220022002300【例】已知某企业的下列资料：要求计算：①该企业第二季度各月的劳动生产率；②该企业第二季度的月平均劳动生产率；③该企业第二季度的总劳动生产率。二）.相对数数列(平均数数列）序时平均数\n解：①第二季度各月的劳动生产率：四月份：五月份：六月份：二）.相对数数列(平均数数列）序时平均数\n③该企业第二季度的劳动生产率：②该企业第二季度的月平均劳动生产率：二）.相对数数列(平均数数列）序时平均数\n复习平均发展水平（序时平均数）时点数列的序时平均数P154-158：1.6，1.7，1.9，2.33.1，3.2\n增长水平\n时间序列的增长水平指标\n逐期增长量累计增长量二者的关系：⒈⒉逐期增长量和累计增长量\n年距增长量：消除季度和月度时间序列中季节波动因素的影响；本期发展水平与上年同期发展水平之差年距增长量\n平均增长量\n增长水平练习P154-158：1.4；3.4（1）【课后作业】\n第三节时间序列的速度分析一、发展速度和增长速度二、平均发展速度和平均增长速度三、速度分析应注意的问题\n时间序列的速度指标辅助的水平指标定基增长速度平均增长速度环比增长速度平均发展速度定基发展速度环比发展速度增长1％的绝对值二、增长速度一、发展速度速度指标\n发展速度和增长速度\n时间序列的发展速度发展水平一般是正数，发展速度也总是一个正数。当发展速度指标值大于0小于1时，表明报告期水平低于基期水平；当发展速度指标值等于1或大于1时，表明报告期水平达到或超过基期水平。一、发展速度:反映发展快慢的相对指标\n发展速度根据采用的基期不同，可分为：时间序列的发展速度\n定基和环比发展速度相互关系时间序列的发展速度\n【例】某产品外贸进出口量各年环比发展速度资料如下:1996年为103.9%，1997年为100.9%，1998年为95.5%，1999年为101.6%，2000年为108%，试计算2000年以1995年为基期的定基发展速度。解：=103.9%*100.9%*95.5%*101.6%*108%=109.57%时间序列的发展速度\n年距发展速度报告期水平与上年同期水平对比达到的相对程度。计算年距发展速度是为消除季节变动的影响。计算公式：季度或者月度时间序列\n增长速度（增长率）利率、收益率本质上是增长速度增长速度指标值有可能为正数，也有可能为负数，负数即负增长。二、增长速度反映增长程度的相对指标，与发展水平相差1。\n增长速度（增长率）增长速度根据采用的基期不同，可分为：\n增长速度（增长率）定基增长速度与环比增长速度之间没有直接的换算关系。需要用发展速度换算（P133例）\n增长速度练习P154-158：1.5；2.5\n平均发展速度和平均增长率\n平均发展速度的计算方法：几何平均法（水平法）高次方程法(累计法)时间序列的平均发展速度平均发展速度：各时期环比发展速度的序时平均数反映社会经济现象较长时期内速度变化的平均水平。\n平均发展速度—环比发展速度的几何平均数。几何平均法环比速度\n总速度几何平均法：只与初末两期水平有关，又称水平法若划分时期且知各时期平均发展速度，则加权几何平均\n解：平均发展速度为：【例】某产品外贸进出口量各年环比发展速度资料如下，1996年为103.9%，1997年为100.9%，1998年为95.5%，1999年为101.6%，2000年为108%，试计算1995年到2000年的平均增长速度。几何平均法：\n几何平均法有关指标的推算:⒈推算最末水平yn：⒉预测达到一定水平所需要的时间n：推算的最末水平与实际资料的最末水平相同。\n高次方程法\n各期定基发展速度之和高次方程法：\n着眼于各期水平累计之和，所以它又称为累计法。因为，可用定基发展速度计算当时，表明现象是递增的；当时，表明现象是递减的。高次方程法：\n【例】某公司2000年实现利润15万元，计划今后三年共实现利润60万元，求该公司利润应按多大速度增长才能达到目的。平均每年增长﹪各年发展水平总和为基期的﹪1年2年3年4年5年14.9114.90246.92398.61572.90773.1715.0115.00247.25399.34574.24991.0415.1115.10247.58400.06575.571075.57高次方程法：\n几何平均法和方程式法的比较:几何平均法研究的侧重点是最末水平；方程法侧重点是各年发展水平的累计总和。1、目的不同。几何平均法侧重考察最末期的水平，时期时点数列均适用；方程式法侧重考察整个发展过程的累计总水平，适用时期数列。2、计算方法不同。几何平均法是求几何平均数，实际上只考虑了最初水平和最末水平。方程式法是解高次方程，考虑的是全期水平之和。3、适用场合不同：末期水平用几何平均，累计量用方程法计算平均发展水平\n1)求平均增长速度，只能先求出平均发展速度，再根据上式来求。平均增长速度：2)平均发展速度的计算方法：几何平均法（水平法）高次方程法(累计法)\n例：某投资银行25年的年利率分别是：1年3%，4年5%，8年8%，10年10%，2年15%，求平均年利率。平均增长速度\n年度化增长率（要点）增长率以年来表示时，称为年度化增长率或年率可将月度增长率或季度增长率转换为年度增长率，计算公式为m为一年中的时期个数；n为所跨的时期总数季度增长率被年度化时，m＝4月增长率被年度化时，m＝12\n年度化增长率（例）【例】1998年3月份财政收入总额为240亿元，2000年6月份的财政收入总额为为300亿元解：m=12，n=27年度化增长率为该地区财政收入的年增长率为10.43%\n年度化增长率（实例）【例】某为期一月的理财产品的年化收益率是4%，计算其一月收益率。解：m=12，n=1年度化增长率与与收益率的关系为该理财产品的月收益率为0.327%\n平均增长速度练习P154-158：1.11；1.12\n增长率分析应注意的问题\n平均增长率分析应注意的问题根据目的选择计算方法。关心最末水平用几何平均法关心发展总和用方程法（仅时期指标）注意社会现象的特点最初水平和最末水平不宜特殊（过高或过低）；\n增长率分析应注意的问题3、分段平均补充说明分析较长时期历史数据特别需要注意4、结合其他指标全面分析发展水平、增长量、环比发展速度、定基发展速度等要结合基期水平——增长1%的绝对值\n增长1%的绝对值：指现象每增长1﹪所代表的实际数量。对增长率分析其补充作用增长率分析应注意的问题\n例：1949年我国的钢铁产量为25万吨，1950年达98万吨，是上年的3.92倍（即增长292%）；1989年生铁产量是5820万吨，1990年高达6238万吨，比上年增长7.18%。增长1%的绝对值\n增长1%的绝对值练习P154-158：2.4\n速度分析应注意的问题【补充】当时间序列中的观察值出现0或负数时，不宜进行速度分析例如：假定某企业连续五年的利润额分别为5、2、0、-3、2万元，对这一序列计算速度，要么不符合数学公理，要么无法解释其实际意义。在这种情况下，适宜直接用绝对数进行分析\n第四节长期趋势变动分析一、时距扩大法二、移动平均法三、数学模型法\n时间序列因素分析\n时间序列时间序列（中国年度、季度GDP）\n指数时间序列指数时间序列（上证综指月K线图）http://q.stock.sohu.com/zs/000001/index_kp.shtml#1\n构成因素和分析模型（1）长期趋势（T）（2）季节变动（S）（3）循环变动（C）（4）不规则变动（I）可解释的变动—不可解释的变动时间序列的构成因素：\n又称趋势变动。是时间序列在较长持续期内表现出来的总态势。是由现象内在的根本性的、本质因素决定的，支配着现象沿着一个方向持续上升、下降或在原有水平上起伏波动。1.长期趋势变动（T）构成因素\n2.季节变动（S）由于自然季节因素（气候条件）或人文习惯季节因素（节假日）更替的影响，时间序列随季节更替而呈现的周期性变动。季节周期：—通常以“年”为周期、—也有以“月、周、日”为周期的—准季节变动。构成因素\n3.循环变动（C）—时间序列中以若干年为周期、上升与下降交替出现的循环往复的运动。如：经济增长中：“繁荣－衰退－萧条－复苏－繁荣”—商业周期。固定资产或耐用消费品的更新周期等。构成因素\n经济系统的内部因素自然因素制度性因素规律性低固定周期循环季节波动成因周期规律变动季节变动和循环变动的比较构成因素\n—由于偶然性因素的影响而表现出的不规则波动。故也称为不规则变动。随机变动的成因：—自然灾害、意外事故、政治事件；—大量无可言状的随机因素的干扰。4.随机变动（I）：构成因素\n时间序列分析模型1.加法模型：假定四种变动因素相互独立，数列各时期发展水平是各构成因素之总和。2.乘法模型：假定四种变动因素之间存在着交互作用，数列各时期发展水平是各构成因素之乘积。\n1.测定各构成因素的数量表现，认识和掌握现象发展的规律；2.将某一构成因素从数列中分离出来，便于分析其它因素的变动规律；3.为时间序列的预测奠定基础。分解分析的作用：时间序列的分解分析\n时距扩大法\n时距扩大法：是测定长期趋势最原始、最简单的方法。将时间序列的时间单位予以扩大，并将相应时间内的指标值加以合并，从而得到一个扩大了时距的时间序列。作用：—消除较小时距单位内偶然因素的影响（互相抵消），显示现象变动的基本趋势。\n时距扩大法：数据大量减少！\n移动平均法\n移动平均法：是测定时间序列趋势变动的基本方法时距扩大法的改良对时间数列的各项数值，按照一定的时距进行逐期移动，计算出一系列序时平均数，形成一个派生的平均数时间数列，以此削弱不规则变动的影响，达到对原序列进行修匀的目的，显示出原数列的长期趋势。\n移动平均法移动平均法简单移动加权移动平均法奇数项移动偶数项移动\n奇数项移动平均法原数列移动平均新数列奇数项简单移动平均\n奇数项简单移动平均新序列比原序列少2项。窗口宽度l：首尾各少(l-1)/2项，共少l-1项\n偶数项简单移动平均偶数项的中心化简单平均数要经过两次移动计算才可得出。例如：移动项数l＝4时，计算的一次移动平均数对应中项在两个时期的中间由于这样计算出来的平均数的时期不明确，故不能作为趋势值。解决办法：对第一次移动平均的结果，再作一次移动平均。\n移动平均移动平均新数列原数列偶数项简单移动平均\n偶数项简单移动平均对于l=2k的移动窗口：1.要取“2k+1”项；2.采用“首尾取半法”计算移动平均数；3.作为2k+1项的长期趋势值。4.比原序列首尾各少k项。\n简单移动平均原数列三项移动平均四项移动平均五项移动平均\n移动平均对数列具有平滑修匀作用，移动项数越多，平滑修匀作用越强；由移动平均数组成的趋势值数列，较原数列的项数少，N为奇数时，趋势值数列首尾各少项；N为偶数时，首尾各少项；简单移动平均的特点\n移动平均的目的是消除短期波动，因此移动间隔应长短适中。移动时间越长，个别观察值的影响越弱，所得趋势值越少，有时会脱离现实；另外丢失的信息（首尾减少的项数）也越大；移动间隔过短，难以消除短期波动；如果现象的发展具有一定的周期性，应以周期长度作为移动间隔的长度。简单移动平均的特点\n5、10、20天均线指数时间序列（上证综指日K线图）\n——555814.5528415.8———566074.0566061.0539793.7496847.3—580819200354813320025692702001580780200046933119994404311998n=4n=3移动平均数产量（y吨）年份例如\n（2）加权移动平均法【补充】加权移动平均法就是根据同一个移动段内不同时间的数据对预测值的影响程度，分别给予不同的权数，再进行移动平均预测长期趋势。简单移动平均法在计算平均值时对移动期内的数据同等看待加权移动平均法根据愈是近期数据对预测值影响愈大这一特点，不同地对待移动期内的各个数据。对近期数据给予较大的权数，对较远的数据给予较小的权数，这样来弥补简单移动平均法的不足。\n（2）加权移动平均法【补充】一般计算奇数项加权移动平均数；权数以二项展开式为基础。中项的权数最大，两边对称，逐期减小。如l=3时，应以（a+b)2=a2+2ab+b2的系数1，2，1为权数：\n又如：l=5时，应以（a+b)4=a4+4a3b+6a2b2+4ab3+b4的系数1，4，6，4，1做为权数。用加权移动平均法求预测值，对近期的趋势反映较敏感，但如果一组数据有明显的季节性影响时，用加权移动平均法所得到的预测值可能会出现偏差。（2）加权移动平均法【补充】\n数学模型法\n数学模型法根据时间序列的数据特征，建立一个合适的数学模型（方程）来描述时间序列的趋势变动，推算各时期的趋势值。建立趋势模型的程序：1.选择合适的模型：判断方法：a.直接观察法（散点图法）b.增长特征法\n1）线性趋势方程—逐期增长量（一阶差分）大致相等。2）二次曲线趋势方程—逐期增长量大致等量递增或递减，二级增长率（二阶差分）大致相等。3）指数曲线方程—环比发展速度近似一个常数。常见的趋势方程[补充]数学模型法\ntyi一阶差分yi-yi-11234na+ba+2ba+3ba+4ba+nb—bbbb直线趋势方程：数学模型法\ntyi一阶差分二阶差分1234na+b+ca+2b+4ca+3b+9ca+4b+16ca+nb+n2c—b+3cb+5cb+7cb+(2n-1)c——2c2c2c抛物线趋势方程：数学模型法\ntyiyi/yi-11234nabab2ab3ab4abn—bbbb指数曲线趋势方程：数学模型法\n逐期增长量大致相等二级增长量大致相等环比发展速度大致相等数学模型法\n（加权）最小二乘法3.计算趋势变动测定值—将自变量t的取值，依次代入趋势方程，求出相应时期的趋势变动测定值。2.估计模型的参数数学模型法\n第五节季节波动和循环波动分析一、季节波动分析二、循环波动分析【补充】\n季节波动分析\n季节变动含义季节变动：在一定时期内由于受自然季节变化或人文习惯因素的影响而形成有规则的周期性的重复变动。特征：有规律的变动；按一定的周期重复进行；每个周期变化大体相同。最大周期为一年，以年份为单位的时间序列一般没有（原始意义上的）季节波动。季节变动分析\n季节变动分析之同期平均法1、同期平均法以若干年资料数据求出同月(季)的平均水平与各年总月(季)水平，进而对比得出各月(季)的季节指数来测定季节变动的程度。季节变动分析\n计算步骤：A、计算各年同月(季)的平均数(i=1~k年，j=1~12月或j=1~4季)（列平均）B、计算各年所有月份(或季度)的总平均数C、计算季节指数SI，同期平均法：直接按月(季)平均法\n例：1）直接平均法：·同期平均法：直接按月(季)平均法\nA、计算第i年平均数；（行平均）B、将历年各月(季)的实际数据同其本年的平均数相比，计算季节比率：(i表示年度，j表示季或月)C、将各年度同期(月或季)的比率进行简单算术平均，求出季节指数Sj同期平均法：比率按月(季)平均法\n同期平均法：比率按月(季)平均法\n年份第一季第二季第三季第四季合计19990.7950.99381.51550.6957420000.81191.00991.46530.7129420010.83820.95591.36760.83834合计2.44512.95964.34842.246912季节指数%81.5098.65144.9574.90400同期平均法：比率按月(季)平均法\n二、趋势剔除法：在具有明显的长期趋势变动的数列中，为了测定季节变动，必须先将趋势变动因素在数列中加以剔除，而后计算季节比率。季节变动分析：移动平均趋势剔除法\n1）对原时间序列求移动平均数，作为相应时期的趋势值T。2）剔除原数列中的趋势变动T，即将原数列各项除以移动平均数的对应时间数据：3）以消除趋势变动后的数列S*C*I计算季节指数，测定季节变动。移动平均趋势剔除法步骤\n例：1999年到2001年某城市旅游人数资料如表所示。某风景旅游城市旅游人数资料试用移动平均趋势剔除法分析季节变动季节变动分析：移动平均趋势剔除法\n季节变动分析：移动平均趋势剔除法\n季节变动分析：移动平均趋势剔除法\n分析：季节指数最高，表明该季为旺季；季节指数最低，表明该季为淡季。调整：季节指数之和必须等于周期长度N（N为季或月），即。当两者不等时，须做相应的调整。调整系数为：经调整，季节指数为：季节变动分析：移动平均趋势剔除法\n循环波动分析\n经济系统的内部因素自然因素制度性因素规律性低固定周期循环季节波动成因周期规律变动季节变动和循环变动的比较循环波动和季节波动的区别\n1、直接法1）测定方法：将每年各季或各月的数值与上年同期进行对比，即求出年距发展速度。它适用于季度和月度时间序列。年距发展速度：循环波动的分析方法\n循环波动分析：直接法2）特点：直接法简便易行，可以大致消除趋势变动和季节变动的影响。主要局限性是忽略了随机波动因素的影响，在消除时间序列长期趋势的同时，相对放大了年度发展水平的影响，当某期发展水平偏低或偏高时，必然会影响C·I的数值，使之偏高或偏低，使得循环波动的振幅被拉大。\n2、剩余法1）剩余法：分解法，利用分解分析的原理，在时间序列中逐次剔除长期趋势变动T、季节变动S的影响，从而得到C·I值。2）计算步骤：A）剔除季节变动，先求季节指数而后剔除季节变动的影响。循环波动分析：剩余法\nB）剔除趋势变动，一般以趋势模型法推算趋势值，剔除趋势值之后求循环变动值CIC）剔除随机变动，对时间序列CI进行移动平均，消除不规则变动I，求得循环波动C具体计算过程中，对时间序列的各个构成要素分解后再剔除，剔除的先后顺序依资料的特点而定。循环波动分析：剩余法\n时间数列的速度分析指标时间数列的水平分析指标发展水平增长量平均发展水平平均增长量增长速度发展速度平均增长速度平均发展速度动态平均指标动态比较指标总结\n影响时间数列变动的因素可分解为：（1）长期趋势（T）（2）季节变动（S）（3）循环变动（C）（4）不规则变动（I）可解释的变动—不可解释的变动总结\n时间序列的分解分析时间序列的分解分析就是按照时间序列的分析模型，测定出各种变动的具体数值。其分析取决于时间序列的构成因素。1.仅包含趋势变动和随机变动（年度数据）：乘法模型为：Y=T×I加法模型为：Y=T+I\n2.含趋势、季节和随机变动：按月（季）编制的时间序列通常具有这种形态。分析步骤：a.分析和测定趋势变动，求趋势值T；b.对时间序列进行调整，得出不含趋势变动的时间序列资料。时间序列的分解分析\nc.对以上的结果进一步进行分析，消除随机变动I的影响，得出季节变动的测定值S。2.含趋势、季节和随机变动：时间序列的分解分析\n长期趋势现象在较长时期内受某种根本性因素作用而形成的总的变动趋势:时距扩大法、移动平均法、数学模型法季节变动现象在一年内随着季节的变化而发生的有规律的周期性变动：同期平均法、趋势剔除法循环变动现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动：直接法、剩余法不规则变动是一种无规律可循的变动，包括严格的随机变动和不规则的突发性影响很大的变动两种类型总结\n课后作业P154-158课后作业：实训题：3;4;6;9