统计学分析总结 7页

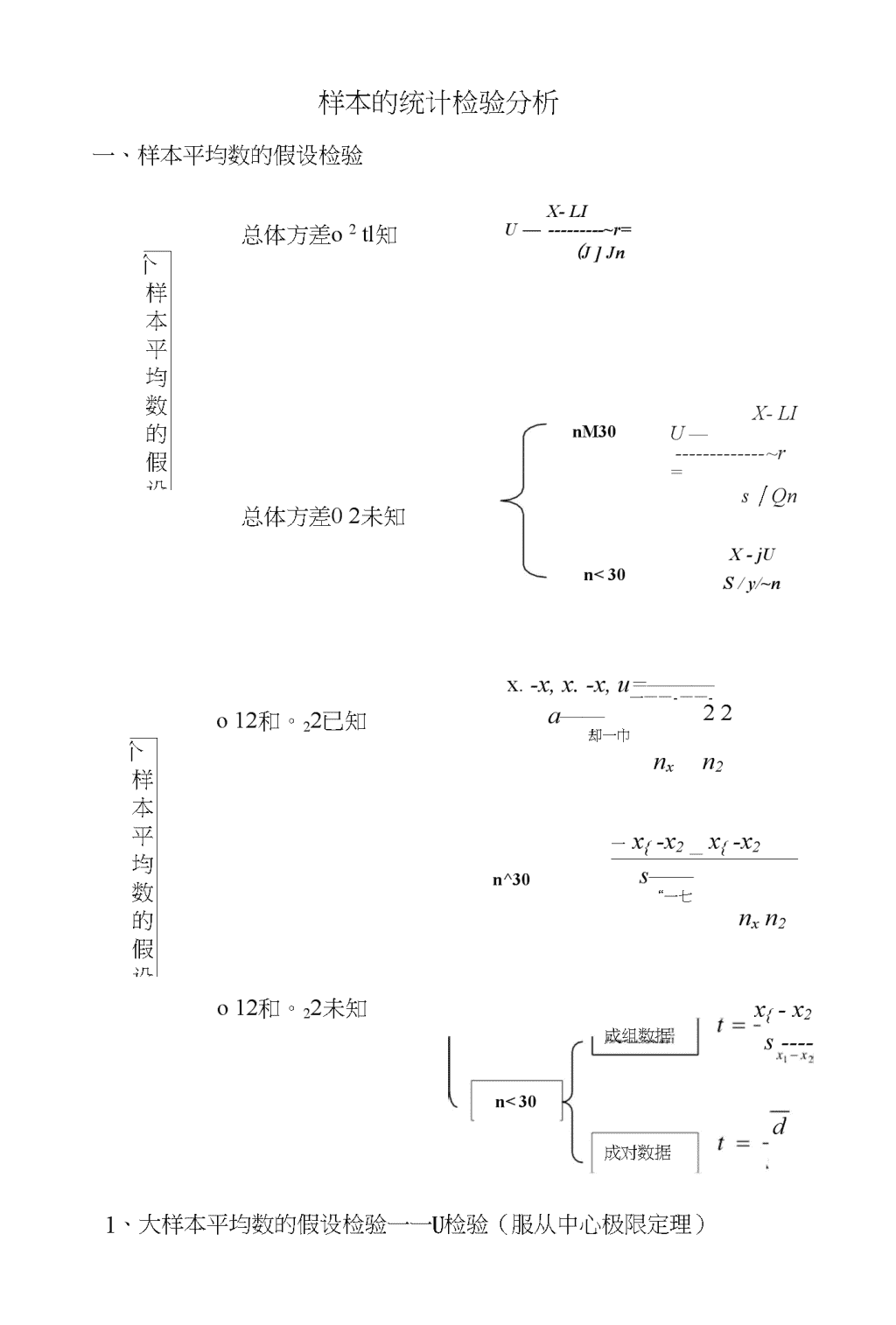
样本的统计检验分析一、样本平均数的假设检验总体方差o2tl知个样本平均数的假设检X-LIU—~r=(J]Jn总体方差02未知nM30X-LIU—~r=s丨Qnn<30X-jUS/y/~no12和。22已知个样本平均数的假设检o12和。22未知x.-x,x.-x,u=———一——-——-a——却一巾22nxn2n^30一x{-x2_x{-x2s——“一七nxn2成组数据dx{-x2sn<30成对数据1、大样本平均数的假设检验一一U检验（服从中心极限定理）\n2、小样本平均数的假设检验一一t检验*单一样本的t检验（遵循自市度df=n-l的t分布）X=——nX-/LIs-X*成组数据平均数的t检验（成组数据两个样本抽自不同总体，两个样本Z间的变量没有任何关联。）oCF2",II1H1I2成组数据s——刁一兀2彳(/1|—1)+£；(直—1)-(“I-1)+(2-1)\Rs-+x】七22S\|S2n,n2df=n-\df=R2(I-/?)222tVl[S2n{n2*配对数据平均数的比较（配对数据的比较耍求两样本间成对，每一\n对除随机地给予不同处理外，其它试验条件应尽量一致。）"一1dsd二、样本方差同质性检验1、一个样本方差的同质性检验——/检验适用范用于检验一个样本所属总体方差02和给定的总体方差0°?是否差异显著。力2=伙_］）二（df=k-l）2、两个样本方差的同质性检验F检验（F检验常常只作右尾检验;F检验是两样本t检验的第一步）适用范用于检验两个样本所属总体方差和。孑是否具有同质c2性。F=—!—(dfi=ni-l・df?二n”l)52…32三、方差分析——对多组样本平均数差异的显著性进行检验1检验可以判断两组数据平均数间的差异显著性，而方差分析既可以判断两组乂可以判断多组数据平均数之间的差异显著性。\n平方和自由度方差F处理间SSt=0：-Cndft=k-l2=idf{2-「2Se处理内SSe=SST—SStdfe=k(n-l)2SS。哦~dfe总变异SST=》J一cdfT=nk-\\n分析・・确定各种原因在总变异处理效应试验误差处理效应试验误差(1)相差不大，说明试验处理对指标影响不大(2)相差较大，即处理效应比试验误差大得多，说明试验处理影响是很人的，不\n最小显著LSD法多重比较LSD0.05=5.05$xl.x2LSDo.oi=to.oi・Sxj.x2新复极公法SSR法:LSR«=SSRa-SXl最小显著LSR法q检验：LSRa=Qa・SxlLSD法的实质是两个平均数相比较的t检验法。LSR法克服了LSD法的局限性，采用不同平均数间用不同的显著差数标准进行比较，它可用于平均数间的所有相互比较。要求：q检验>新复极差法>LSD法，但，当样本数k=2时，LSD法、LSR法和q检验法的显著性尺度是相同的。小结：(1)大样本(n^30)平均数的假设检验一一u检验(2)小样本(n<30)平均数的假设检验一一t检验——独立样本t检验：抽样与％作比较\n——成组样本t检验:成组数据两个样本抽自不同总体,两个样本之间的变量没有任何关联，即两个抽样样本彼此独立O——配对样本t比较:配对数据的比较要求两样本间成对,每一对除随机地给予不同处理外，其它试验条件应尽量一致。（3）平均数的假设检验是建立在方差的同质性检验的基础上(4)离散型资料，即数据为抽样样本统计量一一X?检验eg：实验的两种方法是否一致，两组实验是否相互独立等。是检验实际频数与期望频数的区别。（5）x2检验的用途：1）一个样本方差的同质性检验（数据属于连续变量）2）适合性检验：比较实际观测值与理论数是否符合的假检验3）独立性检验：判断两个或两个以上因素Z间是否具有关联的假设检验（6）方差分析：多组样本总变异的显著性检验对于精度要求高的试验——q检验法一般试验——SSR检验法试验中各个处理均数皆与对照相比的试验一一LSD检验法