统计学回归分析 4页

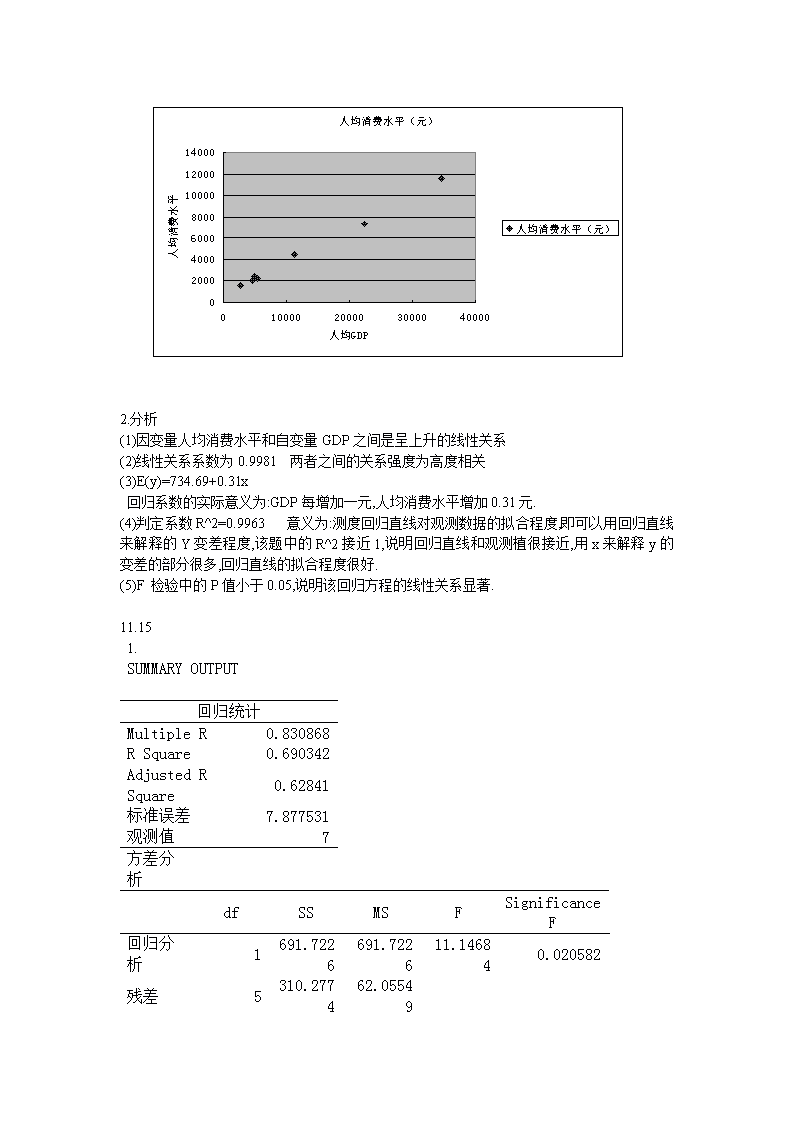
统计学实验报告二习题11.61.图解SUMMARYOUTPUT回归统计MultipleR0.9981RSquare0.9963AdjustedRSquare0.9955标准误差247.3观测值7方差分析　dfSSMSFSignificanceF回归分析181444969814449691331.6923E-07残差530579561159.01总计681750764　　　　Coefficients标准误差tStatP-valueIntercept734.692822139.54035.2650940.003285XVariable10.308682750.00845936.492362.91E-07Lower95%Upper95%下限95.0%上限95.0%375.991093.393375.99305271093.3930.28690.3304270.2869386270.330427\n2.分析(1)因变量人均消费水平和自变量GDP之间是呈上升的线性关系(2)线性关系系数为0.9981两者之间的关系强度为高度相关(3)E(y)=734.69+0.31x回归系数的实际意义为:GDP每增加一元,人均消费水平增加0.31元.(4)判定系数R^2=0.9963意义为:测度回归直线对观测数据的拟合程度,即可以用回归直线来解释的Y变差程度,该题中的R^2接近1,说明回归直线和观测植很接近,用x来解释y的变差的部分很多,回归直线的拟合程度很好.(5)F检验中的P值小于0.05,说明该回归方程的线性关系显著.11.151.SUMMARYOUTPUT回归统计MultipleR0.830868RSquare0.690342AdjustedRSquare0.62841标准误差7.877531观测值7方差分析　dfSSMSFSignificanceF回归分析1691.7226691.722611.146840.020582残差5310.277462.05549\n总计61002　　　　Coefficients标准误差tStatP-valueIntercept29.399114.8072536.1155730.001695XVariable11.5474780.4634993.3386880.020582Lower95%Upper95%下限95.0%上限95.0%17.0416741.7565517.0416741.756550.3560162.7389390.3560162.7389392.分析:(1)E(y)=29.40+1.55x(2)P<0.05所以广告费支出与销售额之间的线性关系是显著的.(3)观察广告费支出与销售额之间的残差图,可以看出,各残差基本位于一条水平带中间,这表明广告费支出与销售额之间的误差项的假设是成立的.(4)选用这个模型.12.11.图解　Coefficients标准误差tStatP-valueIntercept25.028722.278631.123440.298298XVariable1-0.049710.105992-0.469040.653301XVariable21.9281691.472161.3097550.2316242.分析:)E(y)=25-0.05*x1+1.93*x2当x1=200,x2=7时E(y)=28.5112.61.图解回归统计MultipleR0.947362RSquare0.897496AdjustedRSquare0.878276\n标准误差791.6823观测值20方差分析　dfSSMSFSignificanceF回归分析3878035052926783546.696973.88E-08　Coefficients标准误差tStatP-valueIntercept148.7005574.42130.258870.799036XVariable10.8147380.5119891.5913210.131099XVariable20.820980.2111773.8876460.001307XVariable30.1350410.0658632.0503220.0570882.分析(1)E(y)=148.7+0.81*x1+0.82*x2+0.65*x3(2)判定系数R^2=0.89被估计的回归方程所解释的比例是0.89(3)F检验中的P<0.05,所以回归方程的线性关系是显著的.(4)t检验中只有X2对应的P小于0.05,回归系数显著,其他的回归系数不显著.