统计学答案46803 30页

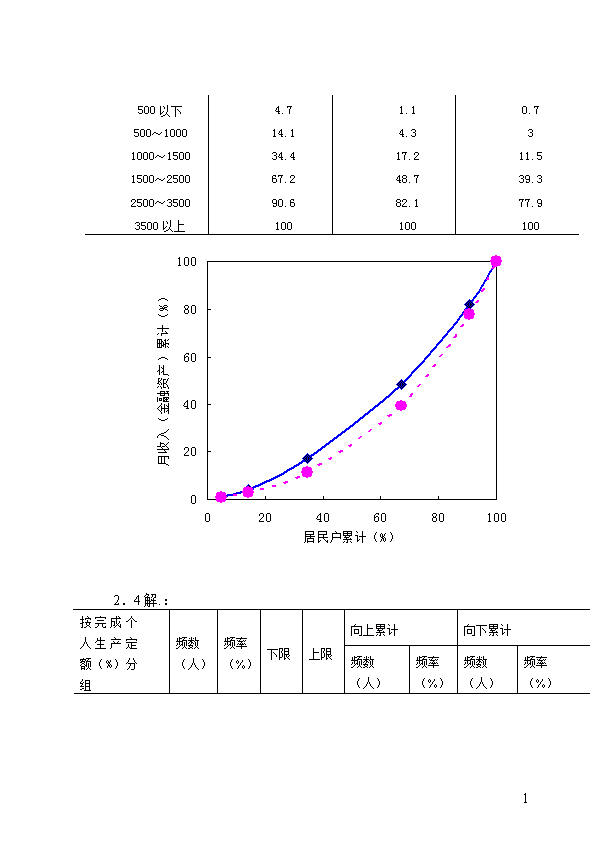
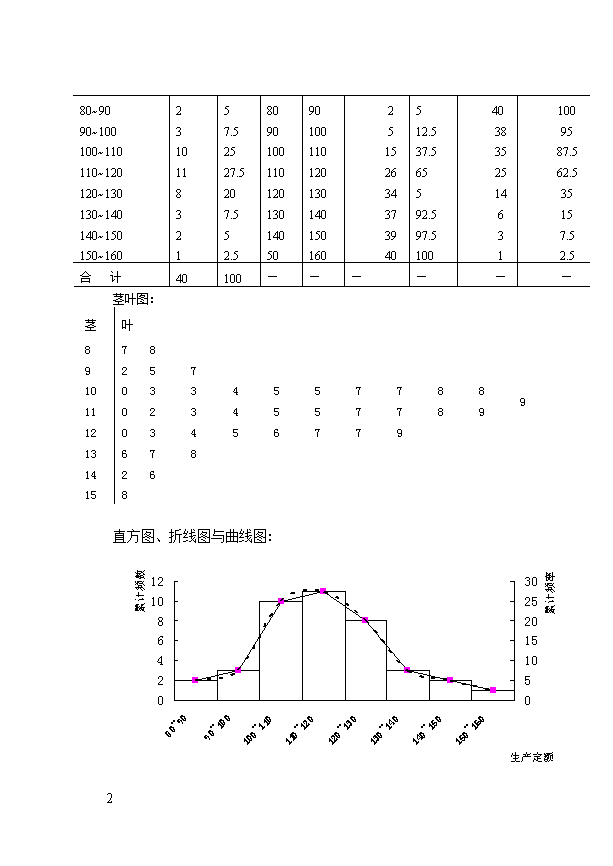
思考与练习第一章1.1判断题：(1)错、(2)错、(3)错、(4)对、(5)错、(6)错、(7)错、(8)对1.2答：民族是定类尺度数据；教育程度是定序尺度数据；人口数、信教人数、进出口总额是定距尺度数据；经济增长率是定比尺度数据。1.3选择题：(1)社会经济统计学的研究对象是：A.(2)属于不变标志的有:（A）属于数量标志的有：（B、C）(3)A1.4答：例如考察全国人口的情况，全国所有的人为统计总体，而每个人就是总体单位。每个人都有许多属性和特征，比如民族、性别、文化程度、年龄、身高、体重等，这些就是标志。其中，性别、民族和文化程度是品质标志，年龄、身高、体重等则是数量标志；而指标是说明统计总体数量特征的，用以说明全国人口的规模如人口总数等指标就是数量指标，而用以说明全国人口某一方面相对水平的相对量指标和平均量指标如死亡率、出生率等指标就是质量指标，质量指标通常是在数量指标的派生指标。1.5（略）第二章2．1：（略）2．2：（1）B（2）D（3）C2．3：按收入分组累计百分数（元）居民户数月收入金融资产29\n500以下4.71.10.7500～100014.14.331000～150034.417.211.51500～250067.248.739.32500～350090.682.177.93500以上1001001002．4解.：按完成个人生产定额（%）分组频数（人）频率（%）下限上限向上累计向下累计频数（人）频率（%）频数（人）频率（%）29\n80~9090~100100~110110~120120~130130~140140~150150~160231011832157.52527.5207.552.58090100110120130140509010011012013014015016025152634373940512.537.565592.597.510040383525146311009587.562.535157.52.5合计40100——————茎叶图：茎叶891011121314157200062885323767334844555655777777988899直方图、折线图与曲线图:29\n由上图可以看出，工人完成个人生产定额属于钟形分布。累计曲线图:第三章3．1（略）3．2（1）B；（2）B、C；（3）A、C；；（4）C。3．313.7元/件3．4解：3．5解：（1）平均利率=存款额=（2）平均利率=存款额=29\n3．6解：0.52750.72633．7：偏度；峰度3．8解：；甲品种更有推广价值。3．9：（1）平均为24.71厘米；（2）众数24.86厘米，中位数24.96厘米；（3）极差24厘米，平均差4.45厘米，标准差5.42厘米。3．10解：优秀率合格率第四章4．1（1）C；（2）A；（3）C；（4）C4．2（1）A、B、C、D（2）A、B、C、E（3）A、B、C、E4．3（1）pr.=0.3;(2)pr.=0.4666674．4pr.=0.8724．5（1）pr.=0.19705;(2)pr.=0.000354．6设三个车间分别记为A1、A2、A3，是次品记为B。则有：p(A1)=25%P(B|A1)=5%p(A1|B)=0.362319p(A2)=35%p(B|A2)=4%p(A2|B)=0.405797p(A3)=40%p(B|A3)=2%p(A3|B)=0.231884与p(A1|B)、p(A3|B)比，p(A2|B)最大，来自乙车间的可能性最大。第五章29\n5.1(1)ABCDE；(2)ABDE;(3)C;(4)B5.2答：因为类型抽样的样本平均数标准差与组间方差无关，决定于组内方差的平均水平；整群抽样的样本平均数标准差与组内方差无关，决定于组间方差大小。所以类型抽样在分组时应尽量提高组间方差，降低组内方差，具体来说，就是使类型抽样的各部分内部单位差异尽可能地小，不同类型间的差异尽可能地大。而整群抽样在分组时为了降低样本平均数标准差，应该设法降低群间方差，可通过提高群内方差方法达到降低群间方差目的。因此，类型抽样与整群抽样对总体进行分组的要求刚好是相反的。5.3由于，样本均值的期望与总值差异为0，样本平均数是总体均值的无偏估计。样本平均数的标准差反映这个无偏估计量本身的波动程度，这个标准差越小，估计量的代表性越强，产生较大偏误的可能性越小；标准差越大，估计量的代表性越差，产生较大偏误的可能性越大。因此，抽样平均数的标准差从整体上反映估计的误差大小，成为该抽样的误差指标。从这个意义上我们建立起平均数与总体均值的内在联系，应用中就是利用样本平均数估计总体平均数的这种内在联系，通过样本平均数去估计总体平均数。5.4答：5.5设这家灯泡制造商的灯泡的寿命为x，则。从而：，不再购买意味着样本平均数小于等于680小时。所求概率Pr.==0.0227529\n第六章6．1(1)D；(2)A;(3)B;(4)B6．2（1）A、C、D、E（2）A、C、E（3）A、B、C6．3(1)N=1500,n=50，样本平均数=560，样本标准差=32.77629806。由于总体标准差未知，可使用样本标准差替代。则重复抽样标准差：。(2)由题意得，=2，月平均工资。所以=[494.45,625.55]6．4(1)已知=4小时，n=100，σ=1.5小时，α=5%。由于样本容量在地区居民人数中所占的比重太小，重复与不重复抽样效果相差不大，按重复抽样计算，区间估计是：因此，95%置信度估计该地区内居民每天看电视的平均时间在3.71到4.29个小时之间。（2）要求极限误差等于27分钟，即Δ=0.45小时。这时概率度：查表知置信度=99.73%6.529\n(1)合格品率：P=190/200100%=95%抽样平均误差：=0.015(2)(3)6．6（1）学生身高的区间估计[169，175.1]（cm）(2)学生身高的区间估计[169.28，175.38]（cm）第七章7.1(1)B;(2)B;(3)C;(4)C7.2(1)A、B、D(2)A、C、D、E7．3(双侧检验)。检验统计量。查出＝0.05和0.01两个水平下的临界值(df=n-1=15)为2.131和29\n2.947。。因为<2.131<2.947，所以在两个水平下都接受原假设。7.4假设检验为（右侧检验）。n=100可近似采用正态分布的检验统计量。查出＝0.01水平下的反查正态概率表得到临界值2.34到2.36之间（因为表中给出的是双侧检验的接受域临界值，因此本题的单侧检验显著性水平应先乘以2，再查到对应的临界值）。计算统计量值。因为z=3>2.36(>2.34)，所以拒绝原假设，认为彩电无故障时间有显著增加。7.5（1）（右侧检验）。，s=450，n=50>30，作大样本处理，检验统计量。＝0.05，=1.65。计算统计量值=1.571348。因为z<，所以样本没有显示新生儿体重有显著增加。（2）p值＝1-P（z<1.571348）=1-0.941949=0.05805>=0.05.接受原假设，样本证据显示新生儿体重没有显著增加。7．629\n当为真时，选择检验统计量查表，因此，在0.05的显著性水平下，可以拒绝原假设，认为平均加油量并非12加仑。(2)计算(1)的p-值。解答：检验的p值为由于，所以拒绝原假设。(3)以0.05的显著性水平来说，是否有证据说明少于20%的驾车者购买无铅汽油？解答：p=0.19当为真时，选择为统计量趋近于标准正态；查表，在显著性水平为0.05的情况下，29\n因此，在显著性水平为0.05的情况下，不能拒绝原假设，没有证据说明少于20%的驾车者购买无铅汽油。(4)计算(3)的p-值。解答：检验的p值为0.4由于，所以不能拒绝原假设。(5)在加油量服从正态分布假设下，若样本容量为25，计算(1)和(2)。解答：当为真时，选择检验统计量查表，因此，在0.05的显著性水平下，可以拒绝原假设，认为平均加油量并非12加仑。并且，检验的p值为由于，所以拒绝原假设。7.729\n解：假设检验为。采用成数检验统计量。查出＝0.05水平下的临界值为1.64和1.65之间。计算统计量值，z＝-0.577>-1.64，所以接受原假设。单侧检验的p值为0.48和0.476之间。显然p值>0.05，所以接受原假设。7.8解：，7.9解：南段28204328121648820北段2011131045151113258差值符号++-+--++-+n+个数＝6n-个数＝4n个数＝10临界值＝9因为6<9，所以认为南段和北段含铁量无显著差异。7.10解：将样本混合排序，有：29\nAB秩A秩B131172183204225246257.5257.52793010.53010.5331234133514361529\n3716381739184019412042214422462347244825502653275428由Excel得：H0:无显著差异；H1:有显著差异取A为总体I，B为总体II，n1=n2=14总体I的秩和T=246alpha＝0.0529\nn=n1+n2=28T平均=n1*(n+1)/2=203标准差=21.76388Z统计量=1.97575临界值＝1.96p值＝0.048183由表可知，Z=1.97575>1.96，且p值=0.048<0.05，所以可以拒绝原假设。7.11解：因为A(8个)，AA(4个)，AAA(2个)，AAAAA(1个)，B(7个)，BB(6个)，BBBB(1个)。n1=27，n2=23。假设检验H0:样本为随机样本，H1:样本为非随机样本。求出游程总和。R1=15，R2=14，R=29。因为，构造统计量。由于=0.05的临界值为1.96，z=0.909<1.96，所以接受原假设。7.12解：：，：；检验统计量是：F=5.285714，相应2.257412。拒绝29\n，认为两总体方差差异显著。资深人员的作用相对稳定，管理人员存在较大差别（结合所了解资料进一步阐述）。7.13解：：性别与偏好不相关；：性别与偏好相关。=6.12，p-值=0.04683<0.05。拒绝原假设，认为性别与偏好相关。第八章8.1(1)D、(2)B、(3)A8．2(1)A、B、C、D、E(2)A、B、C、D8.3离差平方和分解是：SST=SSA+SSB+SSAB+SSE。相对应于SST、SSA、SSB、SSAB和SSE的自由度分别是rnm-1、r-1、n-1、(r-1)(n-1)和rn(m-1)。8.4解：方差分析表：由于P值=0.008819<0.05,所以肥料对农作物的收获量有显著的作用。8.5方差分析表：29\n由于p值=0.11949>0.05,所以品种检验对产量没有显著影响。8.6方差分析表：由于行(地区)因素的p值=0.241868>0.05,所以地区对销售量也没有显著影响。同理，列(包装)因素的p值=0.31943>0.05，所以，包装对销售量没有显著影响。8.7上表中列是工人，行是设备。从P-value可知，无论是工人还是设备对产量都没有显著影响。第九章9.129\n（1）BCD;(2)C;(3)C;(4)ABD9.2证明：教材中已经证明是现行无偏估计量。此处只要证明它在线性无偏估计量中具有最小方差。设为的任意线性无偏估计量。也即，作为的任意线性无偏估计量，必须满足下列约束条件：；且又因为，所以：分析此式：由于第二项是常数，所以只能通过第一项的处理使之最小化。明显，只有当时，才可以取最小值，即：29\n所以，是总体回归系数的最优线性无偏估计量.9.3解：（1）因此，，其中，0.7863为边际成本，表示销售收入每增加一个单位，销售成本平均增加0.7863单位。40.3720为固定销售成本，表示当没有销售收入的情况下仍要花费的销售成本。（2）又，可得回归误差标准差（3）29\n查ｔ分布表可知：显著水平为５％，自由度为10的双侧ｔ检验的临界值是2.228。以上计算的ｔ值远远大于此临界值,所以拒绝原假设,接受备择假设，即认为销售收入对销售成本的影响是非常显著的。（4）把=800代入模型，得（万元）===2.2282查ｔ分布表可知：显著水平为５％，自由度为10的双侧ｔ检验的临界值是2.228。因此，当销售收入为800万元时，置信度为95％的销售成本的预测区间如下：669.41-2.228×2.2282≤Ｙf≤669.41+2.228×2.2282即664.45（万元）≤Ｙf≤674.37（万元）9.4解：(1),Y=0.0727+0.0273x(2)0.071996（3）相关系数29\nｔ＝15.7044≥2.365所以，拒绝原假设。可以得出身高与体重存在显著相关关系的结论。(4)＝≥2.365所以，拒绝原假设。根据样本，可判断体重与身高有显著关系。第十一章11．1（1）A、B、D；（2）A、B、C、E（3）A、B、C、D、（4）B、C、D（5）B、D、E11．2解：①填写表中空格，结果用斜体表示。月份1234月初职工人数（人）月总产值（万元）月平均人数（人）月劳动生产率（元/人）25027.8252651050无资料26.500265100028029.1502751060270———29\n②第一季度平均职工人数==268.33（人）③第一季度工业总产值=27.825+26.500+29.150=83.475（万元）第一季度平均每月工业总产值==27.825（万元）④第一季度劳动生产率==3110.91（元/人）第一季度平均月劳动生产率===1036.97（元/人）11．3解：每年应递增：=118.64%以后3年中平均每年应递增：=114.88%11．4解：第一步：计算十二个月的移动平均修匀值，由于移动项数为偶数项，需进行二次移动平均，结果见下表。十二个移动平均的结果消除了季节变动和随机变动的影响，所得各月的二次移动平均值为趋势变动和循环变动综合作用的结果，即。第二步：剔除趋势变动与循环变动的影响。用各月的实际值分别除以各月的移动平均修匀值，则得到季节变动与随机变动共同作用的结果，即。二次移动平均值结果表月份2000200120022003200429\n1—72.92114.42145.46165.632—73.42116.09146.00164.173—74.38118.38146.88162.754—76.46122.54147.00163.675—83.33128.59148.67164.506—92.92137.34152.00164.50763.75100.83144.42155.96—867.92107.08145.67161.59—970.00110.42146.09164.92—1071.46111.88146.50165.96—1172.25112.92145.75166.50—1272.59113.46145.34166.42—第三步，对第二步的计算结果进行各年同月平均，则消除随机变动的影响，所得结果为各月的季节指数S。第二步、第三步的相应计算结果见下表。如1月份的季节指数：S=（205.7%+209.75%+192.49%+208.3%）/4=204.24%；7月份的季节指数：S=（12.55%+11.9%+22.16%+23.72%）/4=17.59%。月份（%）季节指数S（%）199019911992199319941—205.70209.75192.49208.30204.242—122.58129.2195.89127.92119.003—53.7850.6854.4755.3053.604—32.7032.6420.4127.4928.335—12.0015.558.076.0810.4429\n6—8.618.015.925.477.00712.5511.9022.1623.72—17.59817.6718.6827.4629.70—23.40928.5731.7047.9250.33—39.661069.9775.97102.3984.36—83.2411290.66301.10288.16282.28—290.8112344.40308.48330.26306.45—322.69通过各月季节指数的比较可以看出，1、2、11、12四个寒冷月份的季节指数远高于其它月份，其毛线销量是正常水平的2-3倍，而春、夏季的季节指数非常低，这说明毛线这种产品的需求量季节性非常明显，符合该产品的特性。11．5解：由于数据的波动幅度较大，因而先分别采用三项加权移动平均和平滑系数为0.9的指数平滑法对各期数据进行预测。①取N=3，，根据公式可计算各期的加权移动平均预测值见表中第4栏斜体部分。则2002年的加权移动平均预测值为②用指数平滑法计算各期的预测值，取，则取平滑初始值，则可计算各期的平滑预测值，29\n1984年的预测值：1985年的预测值：同理可得1986-2001年各年的指数平滑预测值，见表中最后一栏斜体部分。则2002年的指数平滑预测值：实际上2002年全社会铁路客运量为105606万人，用指数平滑法预测的相对误差仅为0.49%，预测效果优于加权移动平均预测法.第十二章12.1：（1）C；（2）B；（3）A；（4）C12.2．：（1）（2）12.3：用加权算术平均数指数102.9%，用加权调合平均数指数102.36%，29\n12.4：=110.28%12.5：（1）40亿元；（2）7.84%，31.37亿元（3）8.63亿元12.6：（1）135.95%；307000元（2）307000=190000+11700012.7：106.25%12.8：101.2%12.9：（1）4.7%；（2）用加权算术平均数指数156.02%，加权调和平均数指数141.09%12.10：（1）i技=106.25%；i普=112.5%（2）110.36%（3）110.36%=101.43%×108.80%11.6=1.6+10（4）略（5）11.6×1500=1.6×1500+10×1500即17400=2400+1500012.11：解：指标权数功效系数甲地区乙地区丙地区主要工业产品质量稳定提高率（%）20808868百元总产值利税额（元）30808656可比产品成本降低率（%）10847652全员劳动生产率（元/人）2076886429\n每万元产能消耗（吨）20547784综合指数—74.48465.5排名—213第十三章13.1解(1)ABCD（2）CD(3)B(4)B13.2解（1）根据最大的最大收益值准则，应该选择方案一。（2）根据最大的最小收益值准则，应该选择方案三。（3）在市场需求大的情况下，采用方案一可获得最大收益，故有：在市场需求中的情况下，采用方案二可获得最大收益，故有：在市场需求小的情况下，采用方案三可获得最大收益，故有：根据后悔值计算公式，可以求得其决策问题的后悔矩阵，如下表：后悔矩阵表状态需求大需求中需求小方案方案一0100140方案二200020方案三4002000根据最小的最大后悔值准则，应选择方案一。（4）29\n由于在所有可选择的方案中，方案一的期望收益值最大，所以根据折中原则，应该选择方案一（5）因为方案二的期望收益值最大，所以按等可能性准则，应选择方案二。综上，最后结果如下表：所依据的准则选择的方案最大的最大收益值准则方案一最大的最小收益值准则方案三最小的最大后悔值准则方案一折衷准则（方案一等可能性准则方案二13.3解(1)方案一：期望E(a1)=150变异系数V1=0.5033，方案二：期望E(a2)=140变异系数V2=0.4124，方案三：期望E(a3)=96变异系数V3=0.1443，所以，根据期望值准则，选择方案一；根据变异系数准则，选择方案三。(2)该企业宜采用满意准则，选择方案二。(3)该企业宜采用最大可能准则，选择方案三。13.4解设由于飞机自身结构有缺陷造成的航空事故为,由于其它原因造成的航空事故为，被判定属于结构缺陷造成的航空事故为，则根据已知的条件有：=0.35,=0.65,=0.80,=0.3029\n当某次航空事故被判断为结构缺陷引起的事故时，该事故确实属于结构缺陷的概率为：该事故确实属于结构缺陷的概率是0.5517。13.5解汽车被盗的司机将汽车钥匙留在车内的概率是0.5556。13.6(1)根据现有信息，生产的期望收益值为41.5万元，大于不生产的期望收益值，应选择生产该产品。(2)如果采用自行调查方案，a．得出受欢迎的概率=0.65×0.7+0.35×0.3=0.56，市场受欢迎的后验概率=0.65×0.7/0.56=0.8125，生产的期望收益=80×0.8125-30×0.1875=59.375万元；b．得出不受欢迎的概率=0.65×0.3+0.35×0.7=0.44，市场受欢迎的后验概率=0.65×0.3/0.44=0.4432，生产的期望收益=80×0.4432-30×0.5568=18.75万元（尽管预报不受欢迎，但生产的预期收益仍大于0即不生产情况）。c．因此，如果采用自行调查，其后验分析最佳方案的期望收益=0.56×59.375+0.44×18.75-3=38.5万元，小于先验分析最佳方案的期望收益41.5万元，所以不宜采取此方案。(3)如果采用委托调查，a．得出受欢迎的概率=0.65×0.95+0.35×0.05=0.635，市场受欢迎的后验概率=0.65×0.95/0.635=0.9724，生产的期望收益=80×0.9724-30×0.0276=76.9685万元；b．得出不受欢迎的概率=0.65×0.05+0.35×0.95=0.365，市场受欢迎的后验概率=0.65×0.05/0.365=0.089，选择生产的期望收益=80×0.089-30×0.911=-20.2055万元（选择不生产）。c．因此，如果采用委托调查，其后验分析最佳方案的期望收益=0.635×76.9685+0.365×0-5=43.872万元，大于先验分析最佳方案的期望收益41.5万元，所以应该采用此方案。29\n29