统计学4(60用) 156页

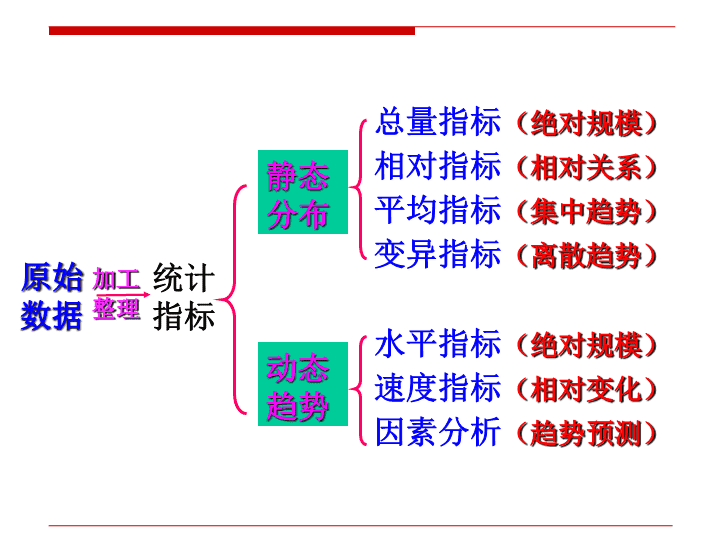
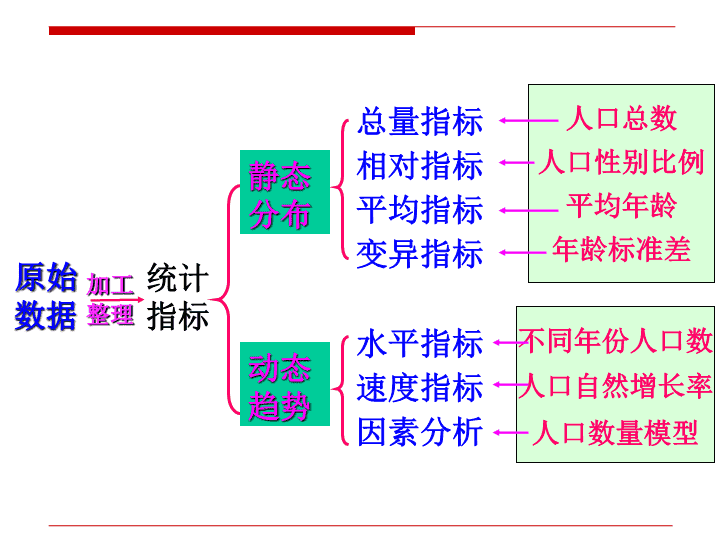
原始数据静态分布动态趋势总量指标（绝对规模）相对指标（相对关系）平均指标（集中趋势）变异指标（离散趋势）水平指标（绝对规模）速度指标（相对变化）因素分析（趋势预测）统计指标加工整理\n原始数据统计指标静态分布动态趋势总量指标相对指标平均指标变异指标水平指标速度指标因素分析加工整理人口总数人口性别比例平均年龄年龄标准差不同年份人口数人口自然增长率人口数量模型\n第四章　综合指标教学目的和要求广义上说，所有的统计指标都可以称为综合指标。根据综合指标数字的表现形式，可将综合指标分为三大类即总量指标、相对指标和平均指标。本章对这三种基本的综合指标作了详细的介绍。通过本章的学习，一般了解各种综合指标的概念、作用及种类，理解各种综合指标的特点和应用场合并熟练掌握其计算方法，能作简单的分析。\n第四章　综合指标★§4.1总量指标§4.2相对指标§4.3平均指标\n§4.1总量指标一、总量指标的概念与作用二、总量指标的基本分类三、计算方法★\n反映现象总体规模或总水平的综合指标，即数量指标，也称为绝对数。总量指标是认识社会经济现象的起点；是实现宏观经济调控和企业经营管理的基本指标；是计算其他统计指标的基础。总量指标的作用：\n§4.1总量指标一、总量指标的概念与作用二、总量指标的基本分类三、计算方法★★\n总体标志总量总体单位总数按反映的总体内容不同分为：总量指标的基本分类按反映的时间状况不同分为：时期指标时点指标按计量单位不同分为：实物指标价值指标劳动指标\n总体标志总量总体单位总量只有可加总体能够计算总体单位总量，不可加总体没有总体单位总量；一个总体中只有一个单位总量，但可以有多个标志总量，它们由总体单位的数量标志值汇总而来。总体单位某一数量标志的标志值总和总体所包含的总体单位的数量\n时期指标时点指标表明现象总体在一段时期内发展过程的总量，如在某一段时期内的出生人数、死亡人数表明现象总体在某一时刻（瞬间）的数量状况，如在某一时点的总人口数具有可加性、数值大小与时期长短有直接关系、需要连续登记汇总不具有可加性、数值大小与时期长短没有直接关系、由一次性登记调查得到\n实物单位自然单位度量衡单位标准实物单位价值单位劳动单位计量单位多个单位的结合运用：复合单位双重单位多重单位（如：人·次、吨·公里）（如：人/平方公里）（如：艘/吨/千瓦）适用范围综合能力差强大小如：台、件如：米、平方米如：标准吨如：工日、工时如：元\n§4.1总量指标概述一、总量指标的概念与作用二、总量指标的基本分类三、计算方法★★★\n计量方法㈠相加计算㈡平衡计算与推算对于同类的计算对象按实际计量单位直接加起来直接相加折算相加对于同类的计算对象按标准计量单位相加如：国内生产总值=总产出－中间投入\n第四章　综合指标★§4.1总量指标§4.2相对指标§4.3平均指标★\n§4.2相对指标一、相对指标的概念及作用二、相对指标的种类三、使用相对指标应注意的问题★\n指是两个有联系的现象数值的比率，用以反映现象的发展程度、结构、强度、普遍程度或比例关系。也称为相对数。相对指标使不能直接对比的现象找到共同的比较基础；用来进行宏观经济管理和评价经济活动的状况。如:反映总体内在的结构特征；用于不同对象的比较评价；反映事物发展变化的过程和趋势等相对指标的作用：\n无名数有名数用倍数、系数、成数、﹪、‰等表示用双重计量单位表示的复名数相对指标的表现形式成数应当用整数的形式来表述3成、近7成8.6成分母为1分母为1.00分母为10分母为100分母为1000主要是用来表现强度相对指标,如:密度.普遍程度.强度等.翻番数：一个数是另一个数的2m倍，即m是番数;(是倍数的一种形式)\n百分点相当于百分数的计量单位，一个百分点就指1﹪。它主要是用绝对数形式表明百分数中1%的个数.上例中，实际比计划多提高的百分点为（7﹪--5﹪）×100=2（个百分点）实际工作中常用，但并不是相对数\n§4.2相对指标一、相对指标的概念及作用二、相对指标的种类三、使用相对指标应注意的问题★★\n相对指标的种类结构相对数比例相对数比较相对数计划完成程度相对数强度相对数动态相对数\n例：我国某年国民收入使用额为19715亿元，其中消费额为12945亿元，积累额为6770亿元。则说明⒈为无名数；⒉同一总体各组的结构相对数之和为1；⒊用来分析现象总体的内部构成状况。\n恩格尔系数＝消费支出中用于食品的支出全部消费支出又如:\n例：我国某年国民收入使用额为19715亿元，其中消费额为12945亿元，积累额为6770亿元。则⒈为无名数，可用百分数或一比几或几比几表示；⒉用来反映组与组之间的联系程度或比例关系。说明\n例：某年某地区甲、乙两个公司商品销售额分别为5.4亿元和3.6亿元。则⒈为无名数，一般用倍数、系数表示；⒉用来说明现象发展的不均衡程度。说明\n是同类指标数值在不同时间上的对比动态相对数⒈为无名数；⒉用来反映现象的数量在时间上的变动程度。说明\n例：某年某地区年平均人口数为100万人，在该年度内出生的人口数为8600人。则该地区一般用﹪、‰表示。其特点是分子来源于分母，但分母并不是分子的总体，二者所反映现象数量的时间状况不同。无名数的强度相对数\n例：某地区某年末现有总人口为100万人，医院床位总数为24700张。则该地区（正指标）（逆指标）为用双重计量单位表示的复名数，反映的是一种依存性的比例关系或协调关系，可用来反映经济效益、经济实力、现象的密集程度等。有名数的强度相对数\n⒈短期计划完成情况的检查⑴计划数与实际数同期时，直接应用公式:A.计划任务数表现为绝对数时\n例：某企业2005年计划产量为10万件，而实际至第三季度末已生产了8万件，全年实际共生产11万件。则⑵考察计划执行进度情况:\n⒉长期计划完成情况的检查⑴累计法计划指标按计划期内各年的总和规定任务\n例：某市计划“十五”期间要完成社会固定资产投资总额60亿元，计划任务的实际完成情况为：年份20012002200320042005合计投资额（亿元）11.411.912.512.813.161.7其中，2005年各月份实际完成情况为（单位：亿元）：月份123456789101112投资额1.11.01.21.11.11.11.21.21.31.10.90.8要求计算：⒈该市“十五”期间固定资产投资计划的完成程度;⒉提前完成计划的时间。已累计完成固定资产投资额60亿元\n解：提前完成计划时间：因为到2005年10月底已完成固定资产累计投资额60亿元（61.7–0.8–0.9=60），即已完成计划任务，提前完成计划两个月。\n例：某市计划“十五”期间要完成社会固定资产投资总额60亿元，计划任务的实际完成情况为：年份20012002200320042005合计投资额（亿元）11.411.912.512.813.161.7其中，2005年各月份实际完成情况为（单位：亿元）：月份123456789101112投资额1.11.01.21.11.11.11.21.21.31.10.90.81.10.8如何确定提前完成计划的时间?思考\n月份123456789101112投资额1.11.11.21.11.11.11.21.21.31.10.80.8【分析】已累计完成固定资产投资额60.1亿元已累计完成固定资产投资额59亿元可以判断出，计划任务应是在2005年10月份的某一天完成的假定10月份每天都完成相等的投资额59亿元60.1亿元601亿元0.1亿元\n在2005年10月为完成尚差的1.0亿元投资额的计划任务需要的天数：【方法一】在2005年10月为完成超额的0.1亿元的投资额所用的天数：【方法二】即提前完成任务两个月零两天。即提前完成任务两个月零两天。\n⑵水平法计划指标以计划末期应达到的水平规定任务⒉长期计划完成情况的检查\n例：某自行车厂计划“十五”末期达到年产自行车120万辆的产量，实际完成情况为：年份20012002200320042005产量（万辆）108114117119123其中，最后两年各月份实际产量为（单位：万辆）：：要求计算：⒈该厂“十五”期间产量计划的完成程度；⒉提前完成计划的时间。月份1234567891011122004年9.69.69.89.89.99.910.010.010.110.110.110.12005年10.110.110.210.210.210.210.210.310.310.410.410.4=120\n解：提前完成计划时间：因为自2004年3月起至2005年2月底连续12个月的时间内该厂自行车的实际产量已达到120万辆〔119+﹙10.1–9.6﹚+（10.1–9.6）=120〕，即已完成计划任务，提前完成计划10个月。\n例：某自行车厂计划“十五”末期达到年产自行车120万辆的产量，实际完成情况为：年份20012002200320042005产量（万辆）108114117119123其中，最后两年各月份实际产量为（单位：万辆）：：月份1234567891011122004年9.69.69.89.89.99.910.010.010.110.110.110.12005年10.110.110.210.210.210.210.210.310.310.410.410.410.010.010.510.5如何确定提前完成计划的时间?思考\n【分析】月份1234567891011122004年9.69.69.89.89.99.910.010.010.110.110.110.12005年10.010.010.210.210.210.210.210.310.310.410.510.5=119.8月份1234567891011122004年9.69.69.89.89.99.910.010.010.110.110.110.12005年10.010.010.210.210.210.210.210.310.310.410.510.5=120.2可以判断出，计划任务应是在2005年3月份的某一天完成的（尚未完成计划）（已超额完成计划）\n2004年3月2005年3月9.8万辆10.2万辆全月轮换将共增加0.4万辆每轮换一天将增加（）万辆在2005年3月份为完成尚差的0.2万辆的计划任务还需要的天数：即提前完成任务九个月零15天。\nB.计划任务数表现为相对数时例：己知某厂2005年的计划规定产品产量要比上年实际提高5﹪而实际提高了7﹪。则\n§4.2相对指标一、相对指标的概念及作用二、相对指标的种类三、使用相对指标应注意的问题★★★\n正确选择对比的基础；指标对比要有可比性；相对指标要与总量指标结合运用；多种相对指标结合运用。使用相对指标应注意的问题\n结构相对数比例相对数比较相对数动态相对数计划完成相对数强度相对数（部分与总体关系）（部分与部分关系）（横向对比关系）（纵向对比关系）（实际与计划关系）（关联指标间关系）多种相对指标应当结合运用\n第四章　综合指标★§4.1总量指标§4.2相对指标§4.3平均指标★★\n§4.3平均指标一、平均指标的概念、特点、作用二、平均指标的种类三、平均指标的计算四、平均指标的测定—变异指标五.是非标志值的平均数与标准差★\n一、平均指标的概念．特点和作用１．平均指标又称统计平均数，用以反映总体各单位某一数量标志在一定时间、地点、条件下所达到的一般水平的综合指标。２．特点（１）把总体各单位标志值的差异抽象化了；（２）平均指标是个代表值，代表总体各单位标志值的一般水平３．作用反映总体各单位变量分布的集中趋势；比较同类现象在不同单位发展的一般水平；比较同一单位的同类指标在不同时期的发展状况；分析现象之间的依存关系等。\n§4.3平均指标一、平均指标的概念、特点、作用二、平均指标的种类三、各平均指标的计算四、平均指标的测定—变异指标五.是非标志值的平均数与标准差★★\n二、平均指标的种类常用的平均指标主要包括两类：1、数值平均数2、位置平均数\n§4.3平均指标一、平均指标的概念、特点、作用二、平均指标的种类三、平均指标的计算四、平均指标的测定—变异指标五.是非标志值的平均数与标准差★★★\n三、平均指标的计算方法㈠算术平均数㈡调和平均数㈢几何平均数㈣中位数㈤众数数值平均数位置平均数★\n1.基本形式：例：直接承担者※注意区分算术平均数与强度相对数算术平均数\n2.强度相对指标与平均指标的区别：①指标的含义不同。强度相对指标说明的是某一现象在另一现象中发展的强度、密度或普遍程度；而平均指标说明的是现象发展的一般水平。②计算方法不同。强度相对指标与平均指标，虽然都是两个有联系的总量指标之比，但是，强度相对指标分子与分母的联系，只表现为一种经济关系；而平均指标是在一个同质总体内标志总量与单位总量的对比。分子是各单位标志值的总和，分母是单位总数，对比结果是反映总体各单位某一标志值的平均数。\n例:下列统计指标属于强度相对指标的是（）。A、平均年龄B、商业网点密度C、人均日产零件数D、人均国民生产总值E、人口自然增长率答案：BDE\nA.简单算术平均数——适用于总体资料未经分组整理、尚为原始资料的情况式中：为算术平均数;为总体单位总数；为第个单位的标志值。3.算术平均数的计算方法\n平均每人日销售额为：3.算术平均数的计算方法某售货小组5个人，某天的销售额分别为520元、600元、480元、750元、440元，则【例】\nB.加权算术平均数——适用于总体资料经过分组整理形成变量数列的情况式中：为算术平均数;为第组的次数；为组数；为第组的标志值或组中值。3.算术平均数的计算方法\n【例】某企业某日工人的日产量资料如下：日产量（件）工人人数（人）101112131470100380150100合计800计算该企业该日全部工人的平均日产量。3.算术平均数的计算方法\n解：3.算术平均数的计算方法若上述资料为组距数列，则应取各组的组中值作为该组的代表值用于计算；此时求得的算术平均数只是其真值的近似值。说明\n分析：成绩（分）人数（人）甲班乙班丙班603915010013950平均成绩（分）619980起到权衡轻重的作用3.算术平均数的计算方法决定平均数的变动范围\n表现为次数、频数、单位数；即公式中的表现为频率、比重；即公式中的3.算术平均数的计算方法指变量数列中各组标志值出现的次数，是变量值的承担者，反映了各组的标志值对平均数的影响程度权数绝对权数相对权数\n4.影响加权算术平均数大小的因素①受单位标志值(变量值)大小的影响。变量值决定平均数的范围；②受各标志值次数的影响，更准确的讲是受个组次数占总次数比重即频率的影响,即受权数的影响.它决定平均数的偏向位置.加权算术平均数的大小受两个因素影响权数的作用：权衡平均数大小.即某一组的次数或频率越大，则该组的标志值对平均数的影响就越大，反之越小。\n(1).变量值与其算术平均数的离差之和衡等于零，即：(2).变量值与其算术平均数的离差平方和为最小，即：5.算术平均数的主要数学性质\n离差的概念12345678-1-1-213\n5.算术平均数的主要数学性质(3).两个独立的同性质变量代数和的平均数等于各变量平均数的代数和。(4).两个独立的同性质变量乘积的平均数等于各变量平均数的乘积。\n思考题力加啤酒公司雇用了468名员工，其中有56名管理人员，130名行政和技术人员，其余282人是工人。这三组人的月平均工资分别是5000元、3000元和2000元。财务主管希望计算全体员工的平均工资。)3(元.3333335000+3000+2000===åNXXi\n正确的计算方法\n二、平均指标的种类及计算方法㈠算术平均数㈡调和平均数㈢几何平均数㈣中位数㈤众数数值平均数位置平均数★★\n【例】设X=（2，4，6，8），则其调和平均数可由定义计算如下：⒉再求算术平均数：⒈求各标志值的倒数：，，，⒊再求倒数：是总体各单位标志值倒数的算术平均数的倒数，又叫倒数平均数调和平均数\nA.简单调和平均数——适用于总体资料未经分组整理、尚为原始资料的情况式中：为调和平均数;为变量值的个数；为第个变量值。调和平均数的计算方法\n【例】设某蔬菜的价格:早0.8元/斤;中0.6元/斤晚0.5元/斤.则(1).早中晚各买一斤,则一天的平均价格为:(2).早中晚各买1元,则一天的平均价格为:这种情况是掌握的资料是各组标志值,且各组的标志总量恰好相等(1元)\nB.加权调和平均数——适用于总体资料经过分组整理形成变量数列的情况式中：为第组的变量值；为第组的标志总量。调和平均数的计算方法\n日产量（件）各组工人日总产量（件）10111213147001100456019501400合计9710【例】某企业某日工人的日产量资料如下：计算该企业该日全部工人的平均日产量。调和平均数的应用掌握的资料是各组标志值和各组的标志总量,而不是各组单位数时,计算平均数应用加权调和平均数形式.\n即该企业该日全部工人的平均日产量为12.1375件。调和平均数的应用解:\n★计算平均指标时如何选择使用加权算术平均数还是使用加权调和平均数计算平均指标时如果已知母项指标，缺子项指标，且计算子项指标时要先做乘法运算，应选择加权算术平均数。如果已知子项指标，缺少母项指标，且计算母项指标时要先做除法运算，应选择加权调和平均数。说明1:\n★在经济统计中加权算术平均数与加权调和平均数的关系说明2:在统计工作中，调和平均数常常被作为算术平均数的变形来使用。经常因为无法直接得到被平均标志值的相应次数的资料而采用调和平均数形式来计算，使用调和平均数的计算结果与加权算术平均数的计算结果相同。\n已知m与f,采用基本平均数公式己知x与f,采用加权算术平均数公式己知x与m,采用加权调和平均数公式比值m与xf令:m=xf\n【例A】某季度某工业公司18个工业企业产值计划完成情况如下：计划完成程度（﹪）组中值（﹪）企业数（个）计划产值（万元）90以下90～100100～110110以上8595105115231038002500172004400合计—1824900计算该公司该季度的平均计划完成程度。\n【例A】某季度某工业公司18个工业企业产值计划完成情况如下：计划完成程度（﹪）组中值（﹪）企业数（个）计划产值（万元）90以下90～100100～110110以上8595105115231038002500172004400合计—1824900计算该公司该季度的平均计划完成程度。分析：应采用加权算术平均数公式计算\n【例B】某季度某工业公司18个工业企业产值计划完成情况如下（按计划完成程度分组）：组别企业数（个）计划产值（万元）实际产值（万元）12342310380025001720044006802375180605060合计182490026175计算该公司该季度的平均计划完成程度。\n【例B】某季度某工业公司18个工业企业产值计划完成情况如下（按计划完成程度分组）：组别企业数（个）计划产值（万元）实际产值（万元）12342310380025001720044006802375180605060合计182490026175计算该公司该季度的平均计划完成程度。分析：应采用平均数的基本公式计算\n二、平均指标的种类及计算方法㈠算术平均数㈡调和平均数㈢几何平均数㈣中位数㈤众数数值平均数位置平均数★★★\n是N项变量值连乘积的开N次方根几何平均数用于计算现象的平均比率或平均速度应用：各个比率或速度的连乘积等于总比率或总速度；相乘的各个比率或速度不为零或负值。应用的前提条件：\nA.简单几何平均数——适用于总体资料未经分组整理尚为原始资料的情况式中：为几何平均数;为变量值的个数；为第个变量值。几何平均数的计算方法\n【例】某流水生产线有前后衔接的五道工序。某日各工序产品的合格率分别为95﹪、92﹪、90﹪、85﹪、80﹪，求整个流水生产线产品的平均合格率。分析：设最初投产100A个单位，则第一道工序的合格品为100A×0.95；第二道工序的合格品为（100A×0.95）×0.92；……第五道工序的合格品为（100A×0.95×0.92×0.90×0.85）×0.80；\n因该流水线的最终合格品即为第五道工序的合格品，故该流水线总的合格品应为100A×0.95×0.92×0.90×0.85×0.80；则该流水线产品总的合格率为：即该流水线总的合格率等于各工序合格率的连乘积，符合几何平均数的适用条件，故需采用几何平均法计算。\n因该流水线的最终合格品即为第五道工序的合格品，故该流水线总的合格品应为100A×0.95×0.92×0.90×0.85×0.80；则该流水线产品总的合格率为：即该流水线总的合格率等于各工序合格率的连乘积，符合几何平均数的适用条件，故需采用几何平均法计算。解\n思考若上题中不是由五道连续作业的工序组成的流水生产线，而是五个独立作业的车间，且各车间的合格率同前，又假定各车间的产量相等均为100件，求该企业的平均合格率。几何平均数的计算方法\n因各车间彼此独立作业，所以有第一车间的合格品为：100×0.95；第二车间的合格品为：100×0.92；……第五车间的合格品为：100×0.80。则该企业全部合格品应为各车间合格品的总和，即总合格品=100×0.95+……+100×0.80几何平均数的计算方法分析：\n不再符合几何平均数的适用条件，需按照求解比值的平均数的方法计算。又因为应采用加权算术平均数公式计算，即\nB.加权几何平均数——适用于总体资料经过分组整理形成变量数列的情况式中：为几何平均数;为第组的次数；为组数；为第组的标志值或组中值。几何平均数的计算方法\n【例】某金融机构以复利计息。近12年来的年利率有4年为3﹪，2年为5﹪，2年为8﹪，3年为10﹪，1年为15﹪。求平均年利率。设本金为V，则至各年末的本利和应为：第1年末的本利和为：第2年末的本利和为：………………第12年末的本利和为：分析：第2年的计息基础第12年的计息基础\n则该笔本金12年总的本利率为：即12年总本利率等于各年本利率的连乘积，符合几何平均数的适用条件，故计算平均年本利率应采用几何平均法。解：\n几何平均数的计算方法思考若上题中不是按复利而是按单利计息，且各年的利率与上相同，求平均年利率。分析第1年末的应得利息为：第2年末的应得利息为：第12年末的应得利息为：…………设本金为V，则各年末应得利息为：\n则该笔本金12年应得的利息总和为：=V（0.03×4+0.05×2+……+0.15×1）这里的利息率或本利率不再符合几何平均数的适用条件，需按照求解比值的平均数的方法计算。因为假定本金为V\n所以，应采用加权算术平均数公式计算平均年利息率，即：解：（比较：按复利计息时的平均年利率为6.85﹪）\n三种不同形式的平均数，有它各自的应用条件，但数量上有一定关系，就同一资料计算时，有：只有当总体全部变量值都相同时，据以计算的三种平均数的数量才会相等。算术平均数。调和平均数与几何平均数的关系\n例：设x取值分别为：４、４、５、５、５、10算术平均与几何平均更为常用一些，其中几何平均数对小的极端值敏感，算术平均数对大的极端值敏感。\n是否为比率或速度各个比率或速度的连乘积是否等于总比率或总速度是否为其他比值是否否是否是几何平均法算术平均法注：数值平均数计算公式的选用顺序指标\n二、平均指标的种类及计算方法㈠算术平均数㈡调和平均数㈢几何平均数㈣中位数㈤众数数值平均数位置平均数★★★★\n是指将总体各单位标志值按大小顺序排列后，处于数列中间位置的标志值，用表示中位数（Median)不受极端数值的影响，在总体标志值差异很大时，具有较强的代表性。中位数的作用：\n如果统计资料中含有异常的或极端的数据，就有可能得到非典型的甚至可能产生误导的平均数，这时使用中位数来度量集中趋势比较合适。比如有5笔付款：9元，10元，10元，11元，60元平均付款为100/5=20元。很明显，这并不是一个好的代表值，而中位数10元是一个更好的代表值。\n中位数的位次为：即第3个单位的标志值就是中位数【例A】某售货小组5个人，某天的销售额按从小到大的顺序排列为440元、480元、520元、600元、750元，则中位数的确定（1）、未分组资料按中位数的含义计算。即先将各标志值按大小排序，再用(n+1)/2确定中位数的位置。当n为奇数时，Me=当n为偶数时，\n中位数的位次为：中位数应为第3和第4个单位标志值的算术平均数，即【例B】若上述售货小组为6个人，某天的销售额按从小到大的顺序排列为440元、480元、520元、600元、750元、760元，则中位数的确定（未分组资料）\n中位数的确定（分组为单值数列）步骤:首先,用确定中位数的位次;其次,逐步向上累计或向下累计至超过中位数位次时,对应的标志值即为中位数.\n【例C】某企业某日工人的日产量资料如下：日产量（件）工人人数（人）向上累计次数（人）10111213147010038015010070170550700800合计800—计算该企业该日全部工人日产量的中位数。中位数的位次：中位数的确定（分组为单值数列）\n中位数的确定（分组为组距数列）步骤:首先,用确定中位数的位次;再次,计算累计次数(向上或向下累计)至大于中位数的位次时,所对应的组即是中位数所在组;然后用近似公式计算中位数的近似值.\n中位数的确定（组距数列）【例D】某车间50名工人月产量的资料如下：月产量（件）工人人数（人）向上累计次数（人）200以下200～400400～600600以上373283104250合计50—计算该车间工人月产量的中位数。\n二、平均指标的种类及计算方法㈠算术平均数㈡调和平均数㈢几何平均数㈣中位数㈤众数数值平均数位置平均数★★★★★\n指总体中出现次数最多的变量值，用表示,它不受极端数值的影响，用来说明总体中大多数单位所达到的一般水平。众数(Mode)有时众数是一个合适的代表值比如在服装行业中，生产商、批发商和零售商在做有关生产或存货的决策时，更感兴趣的是最普遍的尺寸而不是平均尺寸。\n日产量（件）工人人数（人）101112131470100380150100合计800【例A】已知某企业某日工人的日产量资料如下:众数的确定（未分组或单值数列.按众数的意义确定）计算该企业该日全部工人日产量的众数。\n众数的确定（组距数列）确定办法:先按众数定义确定众数组,然后按近似分式计算众数的近似值.Mo:众数;L:众数组的下限;U:众数组的上限;:众数组次数与前一组次数之差(fi-fi-1);:众数组次数与后一组次数之差(fi-fi+1).\n众数的确定（组距数列）【例B】某车间50名工人月产量的资料如下：月产量（件）工人人数（人）向上累计次数（人）200以下200～400400～600600以上373283104250合计50—计算该车间工人月产量的众数。\n众数的原理及应用有83名女生身高原始数据这83名女生身高组距数列\n当数据分布存在明显的集中趋势，且有显著的极端值时，适合使用众数；当数据分布的集中趋势不明显或存在两个以上分布中心时，不适合使用众数（前者无众数，后者为双众数或多众数，也等于没有众数）。众数的原理及应用\n出生1981.01980.01979.01978.01977.01976.01975.0160140120100806040200有400名学生出生时间分布直方图众数的原理及应用没有突出地集中在某个年份\n192.5190.5188.5186.5184.5182.5180.5178.5176.5174.5172.5170.5168.5166.5164.5162.5160.5158.5156.5154.5152.5150.5148.56050403020100众数的原理及应用400名学生的身高分布直方图出现了两个明显的分布中心\n(六).中位数、众数与算术平均数的关系1.中位数、众数与算术平均数之间存在着一定的关系。这种关系，决定于总体内部的次数分配状况。2.对称的次数分配时：3.右(正)偏分布时:左(负)偏分布时:4.不论左偏或右偏,在轻微偏态时,一般有:如:某储蓄所活期存款余额中小于500元的占半数,经测定,出现次数最多的为350元,则活期存款的平均余额为:\n☆位置测度的一种常用方法：百分位数(Percentile)概念：第p个百分位数是这样的数值：至少有p%个数值跟它一样大或比它小；至少有(100－p)%个数值跟它一样大或比它大。例如，一个考生入学考试的口语成绩是54分，对应第70个百分位数，我们就可以知道大约有70%的考生成绩比他低，或者说大约有30%的考生成绩比他高。\n☆位置测度的另一种常用方法：四分位数(Quartile)通常将数据分成四个部分是合乎需要的，每一部分大约包括1/4或25%的数据，分位点称为四分位数。\n☆位置测度的另一种常用方法：四分位数(Quartile)25%25%25%25%Q1Q2Q3把排序数据等分为四个区间Quarters\n§4.3平均指标一、平均指标的概念、特点、作用二、平均指标的种类三、平均指标的计算四、平均指标的测定—变异指标五.是非标志值的平均数与标准差★★★★\n课程学生语文数学英语总成绩平均成绩甲乙丙606555656565706575195195195656565单位：分某班三名同学三门课程的成绩如下：请比较三名同学学习成绩的差异。\n集中趋势弱、离中趋势强集中趋势强、离中趋势弱\n四、平均指标的测定—变异指标(一)、变异指标的含义和作用(二).变异指标的种类及计算(三)、是非标志的标准差及方差★★★\n指反映统计数列中以平均数为中心,总体各个单位标志值的差异程度或离散程度的指标。也称为标志变动度.变异指标即:变异指标值越大，标志值之间的差异程度越大,平均指标的代表性越小；反之，平均指标的代表性越大.作用:1.用来衡量和比较平均数代表性的大小；2.用来反映社会经济活动过程的均衡性和节奏性和稳定性.\n测定标志变异度的绝对量指标（与原变量值名数相同）测定标志变异度的相对量指标（表现为无名数）全距平均差标准差全距系数平均差系数标准差系数标志变异指标的种类★\n指所研究的数据中，最大值与最小值之差，又称极差。全距最大变量值或最高组上限或开口组假定上限最小变量值或最低组下限或开口组假定下限【例A】某售货小组5人某天的销售额分别为440元、480元、520元、600元、750元，则\n【例B】某季度某工业公司18个工业企业产值计划完成情况如下：计划完成程度（﹪）组中值（﹪）企业数（个）计划产值（万元）90以下90～100100～110110以上8595105115231038002500172004400合计—1824900计算该公司该季度计划完成程度的全距。\n优点:计算方法简单、易懂；缺点:易受极端数值的影响，不能全面反映所有标志值差异大小及分布状况，准确程度差往往应用于生产过程的质量控制中全距的特点\n⑴简单平均差——适用于未分组资料是各个数据与其算术平均数的离差绝对值的算术平均数，用A.D表示平均差计算公式：总体算术平均数总体单位总数第个单位的变量值\n【例A】某售货小组5个人，某天的销售额分别为440元、480元、520元、600元、750元，求该售货小组销售额的平均差。解：即该售货小组5个人销售额的平均差为93.6元。\n⑵加权平均差——适用于分组资料平均差的计算公式总体算术平均数第组变量值出现的次数第组的变量值或组中值\n【例B】计算下表中某公司职工月工资的平均差。月工资（元）组中值（元）职工人数（人）300以下300～400400～500500～600600～700700～800800～900900以上2503504505506507508509502083143824563052377820合计—2000\n解：即该公司职工月工资的平均差为138.95元。\n优点:不易受极端数值的影响，能综合反映全部单位标志值的实际差异程度；缺点:用绝对值的形式消除各标志值与算术平均数离差的正负值问题，不便于作数学处理和参与统计分析运算。平均差的特点一般情况下都是通过计算另一种标志变异指标——标准差，来反映总体内部各单位标志值的差异状况\n⑴简单标准差——适用于未分组资料计算公式：总体单位总数第个单位的变量值总体算术平均数是各个数据与其算术平均数的离差平方的算术平均数的开平方根，用来表示；标准差的平方又叫作方差，用来表示。标准差(又称均方差或均方根差)\n【例A】某售货小组5个人，某天的销售额分别为440元、480元、520元、600元、750元，求该售货小组销售额的标准差。解：（比较：其销售额的平均差为93.6元）即该售货小组销售额的标准差为109.62元。\n⑵加权标准差——适用于分组资料标准差的计算公式总体算术平均数第组变量值出现的次数第组的变量值或组中值\n【例B】计算下表中某公司职工月工资的标准差。月工资（元）组中值（元）职工人数（人）300以下300～400400～500500～600600～700700～800800～900900以上2503504505506507508509502083143824563052377820合计—2000\n解：（比较：其工资的平均差为138.95元）即该公司职工月工资的标准差为167.9元。\n标准差的特点不易受极端数值的影响，能综合反映全部单位标志值的实际差异程度；用平方的方法消除各标志值与算术平均数离差的正负值问题，可方便地用于数学处理和统计分析运算.由同一资料计算的标准差的结果一般要略大于平均差。\n简单标准差加权标准差标准差的简捷计算避免离差平方和计算过程的出现目的:变量值平方的平均数变量值平均数的平方\n测定标志变异度的绝对量指标（与原变量值名数相同）测定标志变异度的相对量指标（表现为无名数）全距平均差标准差全距系数平均差系数标准差系数标志变异指标的种类★★\n可比变异系数指标\n身高的差异水平：cm体重的差异水平：kg用变异系数可以相互比较可比\n平均差系数标准差系数变异系数指标用来对比不同水平的同类现象，特别是不同类现象总体平均数代表性的大小:——标准差系数小的总体，其平均数的代表性大；反之，亦然。应用:\n【例】某年级一、二两班某门课的平均成绩分别为82分和76分，其成绩的标准差分别为15.6分和14.8分，比较两班平均成绩代表性的大小。解：一班成绩的标准差系数为：二班成绩的标准差系数为：因为，所以一班平均成绩的代表性比二班大。\n§4.3平均指标一、平均指标的概念、特点、作用二、平均指标的种类三、平均指标的计算四、平均指标的测定—变异指标五.是非标志值的平均数与标准差★★★★★\n是非标志总体分组单位数变量值具有某一属性不具有某一属性10合计—为研究是非标志总体的数量特征，令指总体中全部单位只具有“是”或“否”、“有”或“无”两种表现形式的标志，又叫交替标志是非标志\n是非标志总体的指标具有某种标志表现的单位数所占的成数不具有某种标志表现的单位数所占的成数指是非标志总体中具有某种表现或不具有某种表现的单位数占全部总体单位总数的比重成数\n是非标志总体的指标均值标准差\n是非标志总体的指标方差标准差系数\n【例】某厂某月份生产了400件产品，其中合格品380件，不合格品20件。求产品质量分布的集中趋势与离中趋势。是非标志总体的指标解：\nEND