统计学的哲学思考 27页

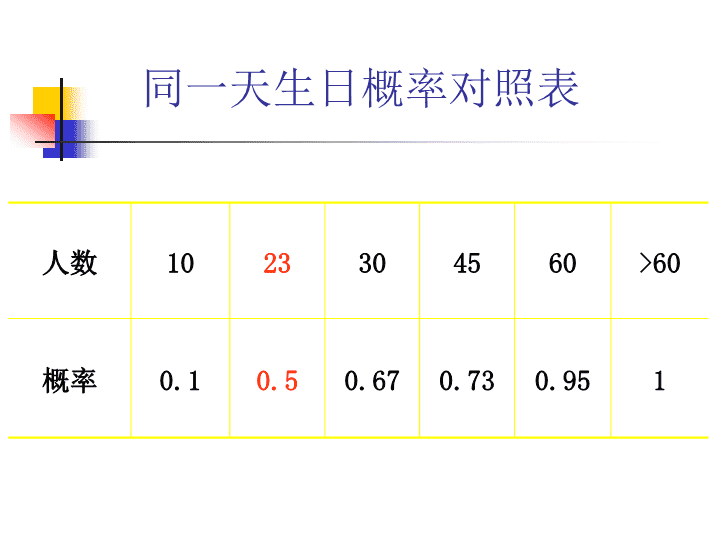
统计学的哲学思考\n统计学的魅力（一）我们来打一个赌：我赌咱们班全部同学中,至少有两个人的生日是同月同日！甚至有可能是同年同于同日！\n同一天生日概率对照表人数1023304560>60概率0.10.50.670.730.951\n有趣的实验从装有相同个数的黑球和白球的口袋中一个个地取球,取后放回,记0为取得黑球,1为取得白球;到内蒙古医院,观察并记录相继在该院出生的婴儿的性别.记M为男婴,F为女婴.我们则得到一个如投掷硬币或随机重复取球所得到的相同的二元符号列.这些随机列，一个是生物学现象白然产生的，另一个是人为产生的.大家猜想一下：两者之间有何关系吗？\n\n\n频数分布数频数期望值男婴白球0546.251273431.252646562.503657062.504302231.255956.25合计200200200.00卡方检验2.225.04\n统计学的魅力（二）上帝投掷硬币来决定人的性别!\n统计的魅力（三）--悲哀的数字原因少活天数原因少活天数未结婚（男性）3500饮酒130未结婚（女性）1600枪炮事故11惯用左手3285自然放射线830%超重1300医疗X-射线620%超重900咖啡6吸香烟（男性）2250口服避孕药5吸香烟（女性）800减肥饮料2抽雪茄330PAP检验—4用烟斗抽烟丝220家里有烟雾警报—10危险工作，事故300带有气垫的轿车—50一般工作，事故74移动冠状动脉监护器—125注：数据来源于Cohen&Lee(1979)的文章\n什么是统计学1.统计工作收集数据的活动2.统计数据对现象计量的结果3.统计学分析数据的方法与技术\n漫画统计它是一种由经验到理性的认识，是一种运用偶然发现规律的科学，无序中深藏有序，偶然中蕴含必然，这是属于统计学的哲学；统计是动态的历史，历史是静态的统计。\n统计学思想远古即存,但作为一门学科历史却不长.统计学无处不在,无论在解开自然奥秘的科学调查中,或是要在日常生活中做出最佳决策或者要解决法庭争端时,统计学都是一种探求真理的必不可少的工具.我们都生活在信息时代,大多数的信息都是以量化的形式传播的.例如:今年的犯罪率与前一年相比下降了10%;明天有30%的可能要下雨;股票市场的道·琼斯指数价格增加了50点;世界上每4个新生婴儿中有一个是中国人;如果你坚持独身,你的寿命要减少8年.所有这些数字对一般公众来说到底意味着什么呢?这些数字里面包含什么样的信息会有助于个人做出正确决策去改进提高他们的生活质量呢?\n漫话统计在终极的分析中，一切知识都是历史在抽象的意义下，一切科学都是数学在理性的基础上，所有的判断都是统计学\n统计学是一门收集、整理和分析统计数据的方法科学，其目的是探索数据的内在数量规律性，用于指导实践，以达到对客观事物的科学认识。Statistics:thescienceofcollecting,analyzing,presenting,andinterpretingdata.Copyright1994-2000EncyclopaediaBritannica,Inc.（不列颠百科全书）\n统计学不只是一种方法或技术，还含有世界观的成分——它是看待世界上万事千物的一种方法，我们常讲某事从统计观点看如何如何，指的就是这个意思。但统计思想（或观点）的养成，不但需要学习一些具体的指示，还要能够从发展的眼光，把这些指示连缀成一个有机的、清晰的图景，获得一种历史的厚重感。——陈希孺《数理统计简史》湖南教育出版社，2002\n统计学没有任何固有的对象，是一门独特的学问。统计学由解决其他领域内的问题而存在并兴旺发达.按萨维奇(L.J.Savage)的说法:统计学基本上是寄生的:靠研究其他领域内的工作而生存，这不是对统计学表示轻视，这是因为对很多寄主来说，如果没有寄生虫就会死。对有的动物来说，如果没有寄生虫就不能消化它们的食物。因此，人类奋斗的很多领域，如果没有统计学，虽然不会死亡，但一定会变得很弱。\n统计中的哲学\n惊人的巧合在一篇发表于美国统计学会杂志(JournaloftheAmericanstatisticalAssociation,Vol.84,p.853-880)的文章中，两个哈佛大学的教授，戴肯斯(Diaconis)和莫斯特雷(Mosteller)证明犷绝大多数的巧合（如一度作为一惊人事件报道的美国某地某人在4个月内赢了两次彩票）是在一定时间内以相当小的概率发生的。统计学中存在一种法则，它是这样叙述的:一次实验中以很小的机会发生的事件，当样本足够大时必然会发生，并可以在任何时候发生而不需要归因于任何特别的理由。\n无序中的有序就像原子和分子的个体游动一样，尽管单个水平下的游动存在不确定性，但对大量个体活动的平均行动来说，我们可以观察到某种稳定性，即会出现“无序中的有序”.概率论中存在被称为大数律的命题，这个命题解释了这种现象.大数律断言，一个系统中多个个体平均行为所显示的不确定性将会随着个体总数的不断增加而逐渐减少，因而可以把这个系统作为一个整体，其表现的几乎是决定性的现象，“越多越保险”这句名言，确实有一个很强的理论基础。大数定律最经典应用：人寿保险。\n随机中的确定性波利亚(Polya)的一段有关一个医生的趣闻例证了一种被称为“赌徒误解”的说法。这个医生安慰他的病人说:你患了一种非常严重的病，患这种病的人只有十分之一能活下来。但是你不必担心，你到我这儿来看病是十分幸运的，因为最近有九个患你这种病的人到我这儿来治疗，他们都去世了。德国哲学家马比(KarlMarbe,1916)就非常坚持这种观点.基于他调查的巴伐利亚州的4个城镇200000个人的出生记录，他总结到:如果过去几天连续出生的女婴相当多的话，就会增加一对夫妇得到男婴的机会。\n另一种与马比的统计安定论类似的观点是另一个哲学家斯特任格尔(O.Sterzinger,1911)提出的“累计理论”。这一观点形成“链法则”，或者说同事件在短时间内容易连续发生这趋势的理论基础。生物学家卡默雷尔(P.Kammerer,1919)把这种观点公式化了。谚语说“祸不单行”，人们总是真诚地接受这个观点并用于一切场合。随机中的确定性\n不确定性知识+所含不确定性量度的知识=可用的知识\n一、平均数———中庸法则平均数,是代表一个群体特性的集中趋势。人生一切行为,应以中庸为法则,既不可过分自我膨胀,也不宜过分自我矮化。认为：平均数的代表性———不偏不激；    平均数的有效性———执两用中；    中央极限———坚守中庸；    平均数的简化性———执简驭繁。\n二、变异数———谨慎法则变异数是指一个群体特性相互差异的程度。人生路上也是高低不平,所谓“世道崎岖,人心险恶”。我们必须有“居安思危”的警觉,处处小心谨慎。认为：误差的累积性———谨小慎微；    误差的传播性———防患未然；    防止误差扩大———把握重点；    事先设计———谋定后动；    及时检验改正误差—切切多检点。\n三、随机抽样———公平法则随机抽样,即是在有限的人力、财力下,以较少样本之特征值,借以推测大量群体之现象。人生有许多事,可用随机抽样方法之旨处理,以收事半功倍之效。认为：随机抽样的代表性———见微知著；随机抽样的同等机会性———公平无私；随机抽样的不确定性——尽人事听天命；大量观察,可靠性加大———多方留意；随机样本,各变量互相独立—人格超然；抽样误差不能避免———求其心安理得。\n四、常态分配———自然法则在统计学中最重要的连续机率分配,其图形称为常态曲线(钟形) ,在自然界出现许多资料,皆用此曲线描述。人生应以自然为法则,自强不息,并应建立中心信仰,以为指针。常态分配的由来———顺应自然；常态分配的普遍性———取道中庸；常态分配的偏态及峰度——不亢不卑；常态分配的所在范围———有容乃大。\n统计学给予我们人生智慧的启发是：平均———中庸之道以为人。  变异———谨小慎微以行事。  随机———公平精神以处世。  大量观察—圆通态度以求实。  常态———崇敬自然以为法。