统计学思维框架new 7页

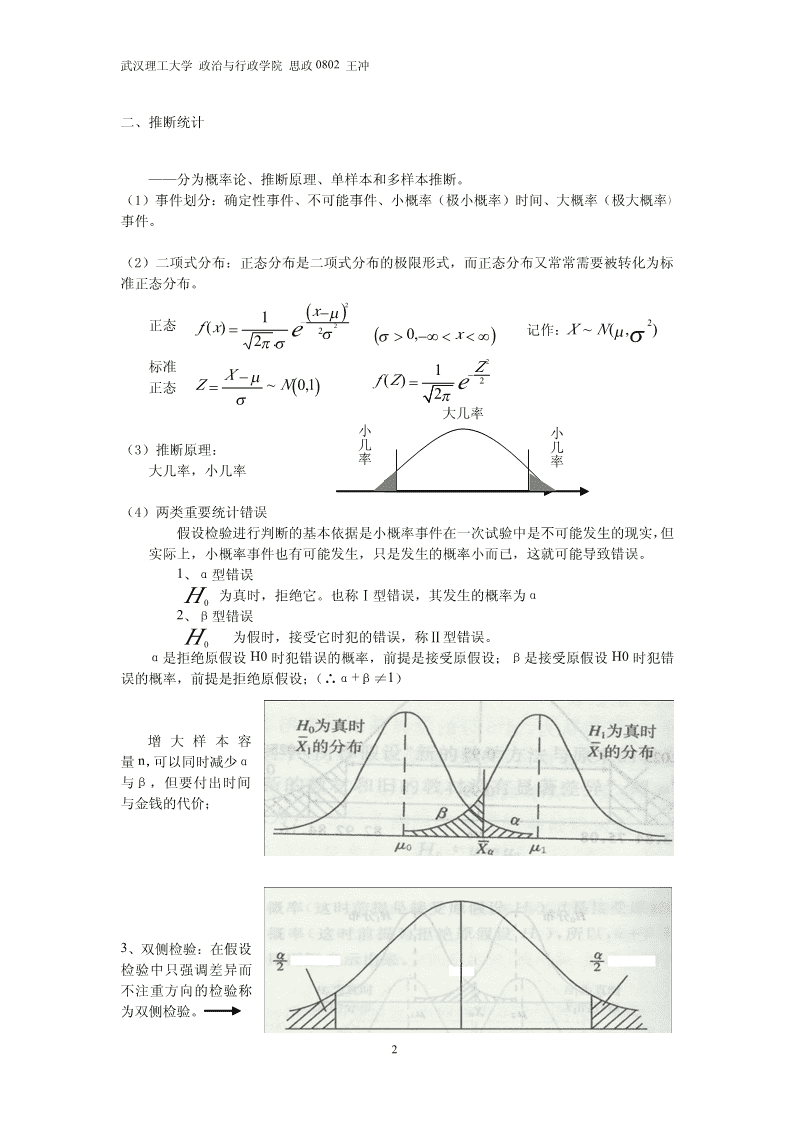
武汉理工大学政治与行政学院思政0802王冲统计学可分为三部分，一是描述统计，二是推断统计，三是实验设计。一、描述统计...................................................................................................................................1（1）集中.................................................................................................................................1（2）离散.................................................................................................................................1二、推断统计...................................................................................................................................2（1）事件划分.........................................................................................................................2（2）二项式分布.....................................................................................................................2（3）推断原理.........................................................................................................................2（4）两类重要统计错误.........................................................................................................21、α型错误.....................................................................................................................22、β型错误.....................................................................................................................23、双侧检验.....................................................................................................................24、单侧检验.....................................................................................................................35、单侧检验与双侧检验的区别.....................................................................................3（5）从样本推断总体.............................................................................................................31、点估计.........................................................................................................................32、区间估计.....................................................................................................................3（6）差异显著性检验.............................................................................................................4（7）方差分析.........................................................................................................................41、组间误差.....................................................................................................................42、组内误差.....................................................................................................................5（8）相关系数与线性回归.....................................................................................................51、相关系数的几何学解释.............................................................................................52、总体无关.....................................................................................................................63、总体相关.....................................................................................................................62（9）X检验.............................................................................................................................6（10）线性回归.......................................................................................................................61、回归方程的求法.........................................................................................................62、判定线性的步骤.........................................................................................................7一、描述统计两个特征——集中与离散：（1）集中。可以运用平均数，或者众数，或者中位数（掌握中位数的计算）反映集中趋势。对于正态分布，三者均可反映集中趋势。但是对于偏态分布，应选择众数。（2）离散。①掌握四分位差、百分位差，二者可以消除极端数对离散程度的影响。②动差是力学上测量力的旋转趋势的名称，统计学用此概念来表示次数分布的离散情况。在动差体系中，一级动差无法用来表示数据分布的差异度。二级动差是用来表示一个分布中离中趋势的指标，也就是“方差”。三级动差是用来表示一个分布中偏斜度或偏态性的指标。四级动差是用来表示一个分布中峰态性的指标。1\n武汉理工大学政治与行政学院思政0802王冲二、推断统计——分为概率论、推断原理、单样本和多样本推断。（1）事件划分：确定性事件、不可能事件、小概率（极小概率）时间、大概率（极大概率）事件。（2）二项式分布：正态分布是二项式分布的极限形式，而正态分布又常常需要被转化为标准正态分布。()2x−µ1−2正态f(x)=σ2记作：e2(σ>0,−∞µH:µ≥µ,H:µ<µ00100010（5）从样本推断总体总体特征：µ，σ。样本特征σX，S参数估计在研究中，根据样本数据的信息来对总体的分布特征行估计，该过程即参数估计。有两种类型参数估计：点估计和区间估计。1、点估计：用样本统计量来估计总体参数。A、无偏性：即用样本统计量估计总体参数时，样本统计量抽样分布的中心等于总体参数。2222σX是µ的无偏估计，S是σ的有偏估计，sn−1是σ的无偏估计。B、有效性：指当总体参数的无偏估计不止一个时，统计量变异（方差）越小，则越有效。C、一致性：指的是样本容量n→∞时，样本估计值越来越接近它所估计的总体参数。D、充分性：指一个容量为n的样本统计量，是否反映了全部n个数据的信息。2、区间估计：指根据样本统计量以一定可靠程度推断总体参数所在的区间范围，它以区间界定总体参数可能出现的范围，它不具体指出总体参数等于多少，但能指出总体参数落入该区间的概率有多大。A、显著性水平：指断定总体参数落在某一区间时，可能犯错误的概率，常以符号α表示。1-α表示置信度或置信水平B、置信区间：也称置信距，是指在某一置信度时，总体参数所在的区间（区域）。2B1、总体方差σ已知，区间估计过程（示意图）2⎛σ⎞X−µX~N⎜µ,⎟Z=~N(0,1)设显著性水平为α，置信度为1-α，则：⎜n⎟σ⎝⎠n⎛⎞⎜X−µ⎟P⎜−Zα≤Z=≤Zα⎟=1−αP⎛σ≤µ≤Xσ⎞1α⎜2σ2⎟⎜X−Zα+Zα⎟=−⎝n⎠⎝2n2n⎠⎡σσ⎤结论：在置信水平为1-α时，总体均值µ的置信区间为⎢X−Zα,X+Zα⎥⎣2n2n⎦3\n武汉理工大学政治与行政学院思政0802王冲2B2、总体方差σ未知，总体µ的区间估计：X−µt=~t(n−1)sn−1n1n2sn−1=n∑(xi−X)−1i=1⎛⎞⎜⎟X−µP⎜tα≤t=≤tα⎟=1−α⎜−(n−1)(n−1)⎟2sn−12⎜⎟⎝n⎠⎡sn−1sn−1⎤结论：在置信水平为α时，µ的置信区间为⎢X−tα(n−1),X+tα(n−1)⎥⎣2n2n⎦（6）差异显著性检验：当遇到2个样本时，便涉及了相关样本均值差异显著性检验(2)∴X~N,µ1σ1(22)d=X−Y~Nµ1−µ2,σ1+σ2−2ρσ1σ2(2)Y~Nµ2,σ2⎛σ2+σ2−2ρσσ⎞d−(µ1−µ2)~N(0,1)d~N⎜µ−µ,1212⎟22⎜12n⎟σ1+σ2−2ρσ1σ2⎝⎠n22d−(µ1−µ2)当σ1、σ2未知时，t=~t(n−1)Sdn−122∑(di−d)22(X−Y)−(µ−µ)Sd==S1+S2−2rS1S112~t(n−1)nSd2()2n−12∑(xi−X)2∑yi−YS1=S2=nn（7）方差分析——用于应对三个样本的情况。F=组件误差/组内误差=（心理效应+组内误差）/组内误差=σ/σxi用平均值来估计总体的标准差，用组内平均差的品均值估计组内误差k22σ1、组间误差=n∑(x−µ−)/(k−1),σ=nŜ（中心极限定律）ii=1xk2∑(xi−µ)xi=1σx==Ŝ,组间自由度dfb=k-1k−14\n武汉理工大学政治与行政学院思政0802王冲2kn(xx−)∑∑ijii=1j=1n−12、组内误差σ=，组内自由度dfw=k(n-1)xik通过f分布对心理效应进行检验，当f值落在f>1的范围内，存在组间效应；否则不存2在组间效应。求得f分布之后要对检验的有效性进行检验，有w、效应量d进行有效性检验，再用N-K检验法和HSD检验检验出现差异的样本。df(1)F−22B若w>30%,则检验有效，否则检验无效。w=df(1)F−+NBxix−jN-K检验法：q=，kn22MSW(1+1)MSW=Kn(−1)σij=∑∑(xij−xi)2ni=1j=11n2若q落在有差异的区间之内，说明第i组和第j组之间存在差异。MSW11HSD，(X1-X2)的临界值=q(+)，若两组的平均值只差大于临界值，则2n1n2两样本存在差异。进行方差分析时要注意天花板效应和地板效应。方差分析最多只能进行3*3*3的分析（8）相关系数与线性回归1、相关系数的几何学解释⎛−x⎞⎛y−y⎞⎜x1⎟⎜1⎟⎜x−x⎟⎜y−y⎟⎜2⎟⎜2⎟⎜M⎟⎜M⎟向量A=⎜⎟向量B=⎜⎟⎜M⎟⎜M⎟⎜x−x⎟⎜y−y⎟⎜n⎟⎜n⎟⎜⎟⎜⎟⎝⎠⎝⎠n∑(xi−x)(yi−y)i=1γ=表示相量A和B之间的夹角的余弦，可以和二维的对比理解nσσxy5\n武汉理工大学政治与行政学院思政0802王冲相关系数的差异性检验，分为两个总体相关和无关两种情况2、总体无关：相关系数服从正态分布N（µ，）µ=0γσγγ21−γ当样本容量n>50或n>30时，σγ=，将γ转化为z分布，进行检验。n−121−γ当样本容量n<50时,σγ=,将γ转化为t分布，进行检验。n−21+γ3、总体相关：样本的γ满足偏态分布，通过费舍z变换zγ=ln，将偏态分布转换为1−γ1+γ1标准正态分布N(μ,σ)。µ=ln(γ为总体的相关系数)，σ=。1−γN−3相关系数的应用条件：两列数据呈正态分布；两列数据满足线性条件。相关系数的应用：尼古丁效应k2(−)222oiEiχ（9）X检验χ=∑通过的值判断数据的分布是否与期望值相符。j=1EI（10）线性回归1、回归方程的求法，确定系数和不确定系数n∑(xi−x)(yi−y)σy=a+bx,b=i=1=γy,a=ybx−n2σx∑(xi−x)i=1nn22∑(xi−x)∑(yi−y)i=1，i=1σ,σ,用修正量时，自由度为n-2，即σ=σ=yxxyn−2n−2n2∑(y−y)2i=1确定系数γ=，表示线性方程的有效性n2∑(y−y)ii=1n2∑(y−y)2ii=1不确定系数1−γ=n，表示线性方程的不确定性。2∑(y−y)ii=16\n武汉理工大学政治与行政学院思政0802王冲2、判定线性的步骤：A划散点图，判断趋势，判断线性性，即利用相关系数的第一个条件；B判断数据是否满足正态分布；C求相关系数；D相关系数差异性检验；E球回归方程。7