计量经济学计算机作业 11页

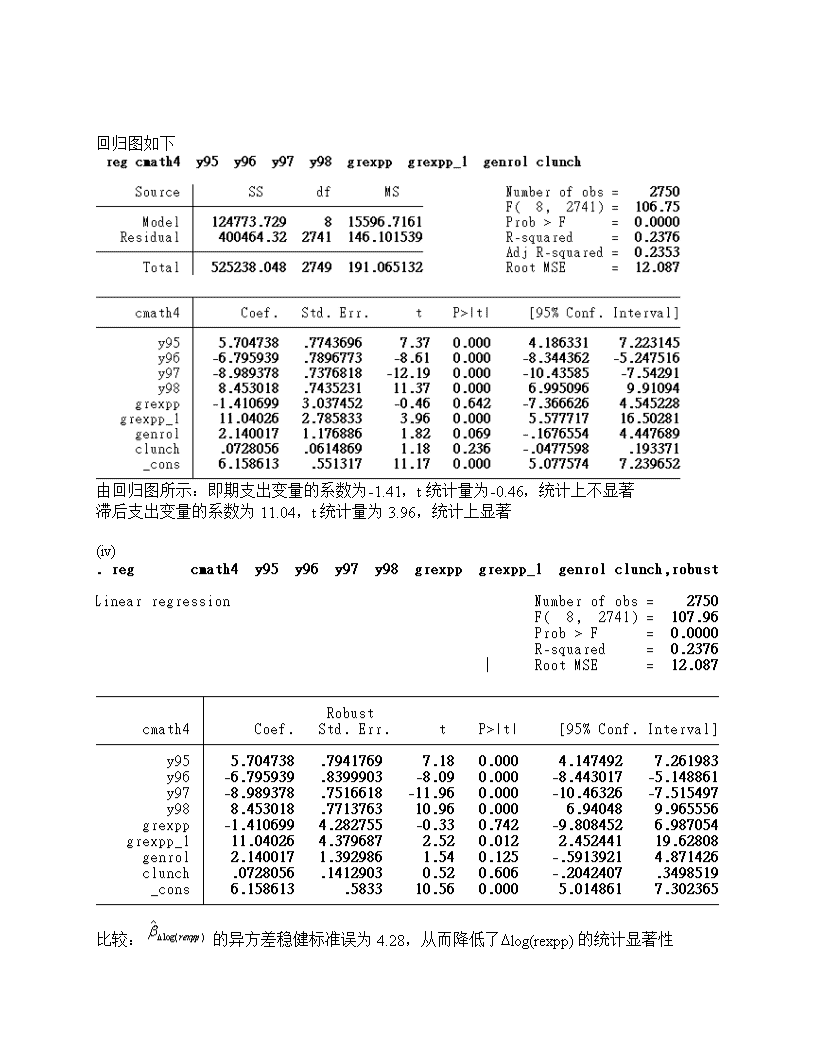
数量经济学付欢计量经济学计算机作业C13.11(i)在其他自变量不变的情况下：根据：log(X1)-log(X0)≈(X1-X0)/X0=△X/X0Dmath4it=b1Dlog(rexppit)=(b1/100)*[100*Dlog(rexppit)]»(b1/100)*(%Drexppit).因此if%Drexppit=10,thenDmath4it=(b1/100)*(10)=b1/10。所以，平均每个学生的真实支出提高10%，则math4it约改变b1/10个百分点。(ii)用一阶差分估计第一部分中的模型（包括1994-1998年度虚拟变量）Dmath4=5.95+.52y94+6.81y95-5.23y96-8.49y97+8.97y98(0.52)(0.73)(0.78)(0.73)(0.72)(0.72)-3.45Dlog(rexpp)+0.635Dlog(enroll)+0.025Dlunch(2.76)(1.029)(0.055)当rexpp增加10%，math4降低0.35%(3.45/10»0.35)(iii)在模型中添加支出变量的一阶滞后,并利用一阶差分估计得Dmath4=6.16+5.70y95-6.80y96-8.99y97+8.45y98(0.55)(0.77)(0.79)(0.74)(0.74)-1.41Dlog(rexpp)+11.04Dlog(rexpp-1)+2.14Dlog(enroll)(3.04)(2.79)(1.18)+0.073Dlunch(0.061)n=2,750,R2=0.238.\n回归图如下由回归图所示：即期支出变量的系数为-1.41，t统计量为-0.46，统计上不显著滞后支出变量的系数为11.04，t统计量为3.96，统计上显著(iv)比较：的异方差稳健标准误为4.28，从而降低了Dlog(rexpp)的统计显著性\n的异方差稳健标准误为4.38，其t统计量降低为2.52。在1%的显著性水平双侧检验下Dlog(rexpp-1)仍然是统计显著的。(t统计量大于1.96)(v)异方差序列相关稳健标准误为4.94，Dlog(rexpp)的t统计量降低了。的标准误为5.13,Dlog(rexpp-1)的t统计量为2.15.双侧检验的p值为0.032(vi)使用1995,1996,1997,1998年进行混合的OLS可得-0.423这表明差分误差有很强的负序列相关(vii)基于充分稳健的联合检验，如下图\n所以模型中没有必要包含学生注册的人数和午餐项目变量C14.10(i)根据回归可知利用混合OLS估计的β1=0.36,当Δconcen=0.10，则Δlfare=0.36*0.10=0.036.airfare增加3.6%、(ii)β1的95%的置信区间为[0.309,0.419]只有当复合误差序列无关，得出的标准误才是有效的,所以有点不太可能，充分稳健下的95%的置信区间为[0.245,0.475],条件为允许存在序列相关和异方差,所以充分稳健下的置信区间比一般的置信区间要大。忽略序列相关会导致参数估计产生不确定性.(iii).斜率变为正斜率的log(fare)的值为0.902/[2*0.103]≈4.38。dist的值为exp(4.38)=80.。该值表示的是fare对dist的正弹性系数。(iv)β1的RE估计值为0.209，表示fare与concern之间正相关。因为t=7.88估计值统计上显著\n(v)FE估计值为0.169，RE的λ估计值为0.9.我们可以预计RE估计值与FE估计值非常相似。\n(vi)在一个航班线上的两个机场附近的城市影响航行的因素为人口，教育水平，雇主类型等。高速路及铁路的便利情况及周围的地理环境，可以考虑为固定不变的。这些因素和concern相关。(vii)考虑到无法观测效应，我们可以使用固定效应模型得出估计值为正，且统计上显著。用FE估计得到的估计值为0.169concern与时间常量正相关C15.8(i)OLS估计方程:n=9,275,R2=0.180Pira=-0.198+0.054p401k+0.0087inc-0.000023inc2-0.0016age+0.00012age2(0.069)(0.010)(0.0005)(0.000004)(0.0033)(0.00004)p401k的系数表示保持收入和年龄不变的情况下，参加401（K）计划与拥有一个个人退休金账户的比没有参加401（K）计划与拥有一个个人退休金账户的概率多0.054。(ii)在上题的回归方程中，保持收入和年龄不变下，在给定的收入和年龄等级中，该方程并不能解释不同的人有不同的储蓄计划。而是解释了储蓄的人会参加401（k）计划和（IRA）计划.在保持其他条件不变的情况下，如果无法控制个人的储蓄计划，用普通的OLS估计无法得到我们想要的结果(iii)欲使e401k成为p401k的有效IV,应该满足两个条件:e401k对p401k有偏效应和e401k0与u无法观测的储蓄计划不相关.如果雇主会提供401（k）退休计划的，工人会储蓄。则u与e401（k）相关。(iv)p401(k)的约简型方程P401k=0.059+0.689e401k+0.0011inc-0.0000018inc2-0.0047age+0.000052age2\n(0.046)(0.008)(0.0003)(0.0000027)(0.0022)(0.000026)n=9,275,R2=.596e401k的系数表示，在保持收入与年龄不变的情况下，有资格参与一项401（k）计划的人参加401（k）的计划会多0.69，明显的是，e401k符合成为p401k工具变量的两个要求之一。(v)用e401k作为p401k的工具变量来估计Pira=-0.207+0.021p401k+0.0090inc-0.000024inc2-0.0011age+0.00011age2(0.065)(0.013)(0.0005)(0.000004)(0.0032)(0.00004)n=9,275,R2=0.180\nIV估计出来的bp401k0.021低于OLS估计值0.054的一半。相应的t统计量值为1.56.约简型中就是给定无法观测的储蓄计划下的估计值。但是我们仍然无法估计参加401（K）计划与拥有个人退休金账户之间的替换关系。C17.11(i)参加劳动的妇女的比率为3286/5634(总数)=0.583.(ii)只利用工作女性的数据用OLS估计工资方程:\nlog(wage)=0.649+0.099educ+0.020exper-0.00035exper2-0.030black+0.014hispanic(0.060)(0.004)(0.003)(0.00008)(0.034)(0.036)n=3,286,R2=0.205平均来说与非黑种人及非西班牙人群组相比，黑种多赚3%，西班牙人多赚1.3%,联合F检验的p值为0.63.所以当控制教育及经验水平下，不同种族之间工资差别不明显。(iii)nwifeinc的系数为-0.0091，t统计量为-13.47，kidlt6的系数为-0.5且t统计量为-11.05我们期待这两个系数为负。如果一个女人的丈夫赚更多的，她不太可能工作。有一个年轻的孩子在家庭中也降低了概率的女人。每个变量是非常显着。(iv)我们需要至少一个影响参加劳动的变量，这个变量并不会直接影响工资的多少。所以,我们必须假定,控制教育、经验和种族差异变量下,其他收入和有一个孩子的情况并不不影响工资。如果雇主歧视有小孩或是丈夫有工作的妇女。这些假定就不会成立。此外,如果有一个孩子会降低劳动力,也就是说她必须花时间去照顾生病的孩子。这样，我们就不能从工资方程中遗漏掉kidlt6。(v)每个观测的逆米尔斯比为1.77，相应的双侧p值为0.77.在3286个观测中，它并不是特别小的，的检验并没有提供有力的证据对零假设没有选择偏差。。\n(vi)把逆米尔斯比加到工资方程中去，斜率系数并没有改变多少。例如,education的系数从0.099变动到0.103，同样在OLS估计下的95%的置信区间内[0.092,0.106]。exper的系数变化很小，black和Hispanic的系数变化很大，但是这些估计值在统计上并不显著。最重要的变化是在–截距估计从[649,539]：从0.649变化到0.539.在本例中，截距为log(wage)的非黑人非西班牙裔妇女且没有受过教育和工作经验的估计值。在全样本下并没有一个妇女是这种情况的。因为斜率系数会发生改变,我们不能说,Heckman估计意味着与没有修正的估计相比，工资水平会更低。C18.5(i)估计的方程如下：hy6t=0.078+1.027hy3t1-1.021Dhy3t-0.085Dhy3t1-0.104Dhy3t2(0.028)(0.016)(0.038)(0.037)(0.037)n=121,R2=0.982,=0.123.使用t检验原假设H0:b=1的t统计量为(1.027 –1)/0.0161.69.在5%的显著性水平下的使用双侧检验中，我们不能拒绝H0:b=1，但在10%的水平上我们会拒绝原假设(b=1)。\n(ii)估计的误差纠正模型如下：=.070+1.259Dhy3t1-.816(hy6t-1–hy3t2)(.049)(.278)(.256)+.283Dhy3t2+.127(hy6t-2–hy3t3)(.272)(.256)n=121,R2=.795.这两个变量的F检验的联合显著的F值为1.35,相应的p-值=0.264,不显著