大学物理 (231) 13页

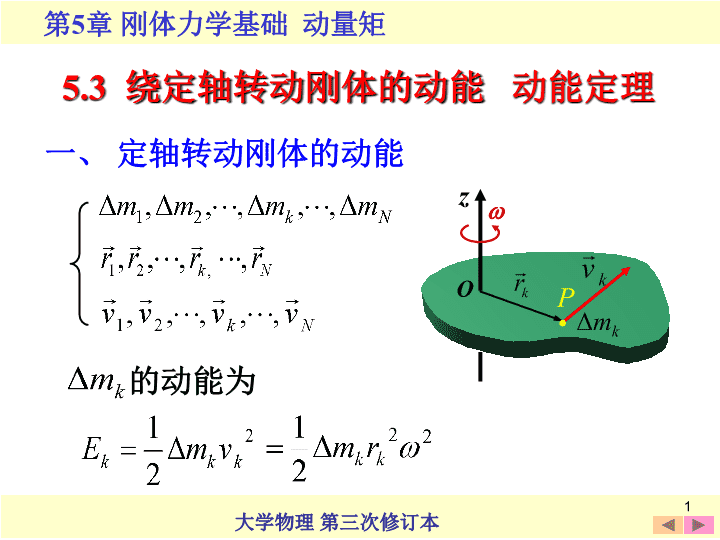
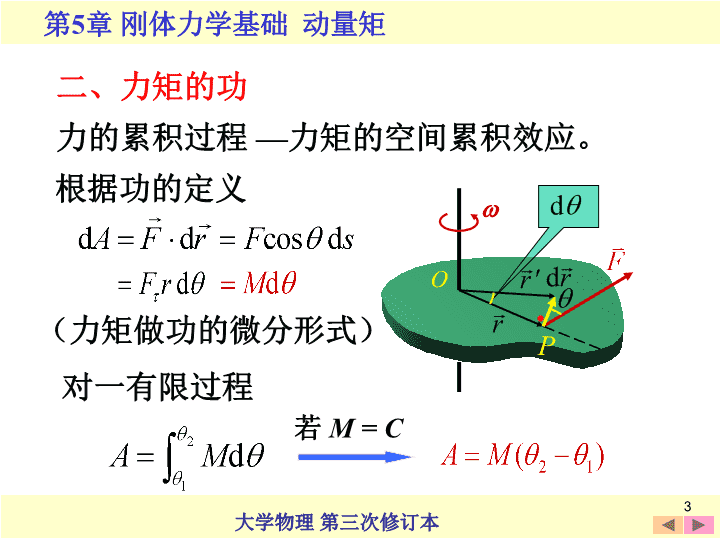
5.3绕定轴转动刚体的动能动能定理一、定轴转动刚体的动能zO的动能为P•1\n绕定轴转动刚体的动能等于刚体对转轴的转动惯量与其角速度平方乘积的一半。刚体的总动能2\n二、力矩的功O根据功的定义（力矩做功的微分形式）对一有限过程若M=C力的累积过程—力矩的空间累积效应。.P3\n(2)力矩的功就是力的功。(3)内力矩作功之和为零。(1)合力矩的功讨论(4)力矩的功率力矩的功率可以写成力矩与角速度的乘积。4\n三、绕定轴刚体的动能定理（合力矩功的效果）元功5\n对于一有限过程绕定轴转动刚体在任一过程中动能的增量,等于在该过程中作用在刚体上所有外力矩所作功的总和。绕定轴转动刚体的动能定理。即6\n(3)刚体动能的增量，等于外力的功。(2)刚体的内力做功之和为零。(1)质点系动能变化取决于所有外力做功及内力做功。讨论7\n刚体重力势能定轴转动刚体的机械能质心的势能对于包括刚体的系统，功能原理和机械能守恒定律仍成立。四、刚体的机械能8\n例1长为l,质量为m的均匀细直棒，可绕轴O在竖直平面内转动,初始时它在水平位置。解由动能定理求它由此下摆角时的。OlmCx9\n此题也可用机械能守恒定律方便求解。而OlmCx10\nh例2一个质量为M,半径为R的定滑轮(当作均匀圆盘)上面绕有细绳,绳的一端固定在滑轮边上，另一端挂一质量为m的物体而下垂。忽略轴处摩擦。ORmM求物体m由静止下落高度h时的速度。圆盘对中心轴的转动惯量11\n绳与圆盘间无相对滑动v=Rω利用刚体的动能定理,得圆盘受力矩FTR作用解hORmM由质点的动能定理：12\n解法2.根据机械能守恒定律hORmM13