大学物理 (10) 31页

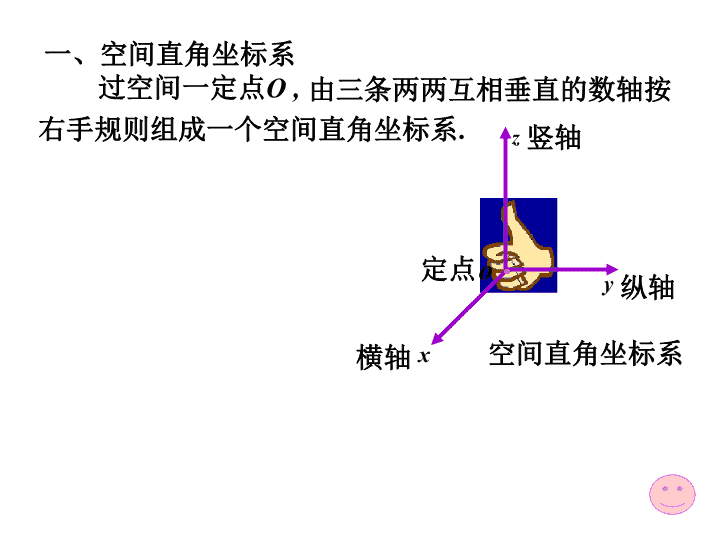
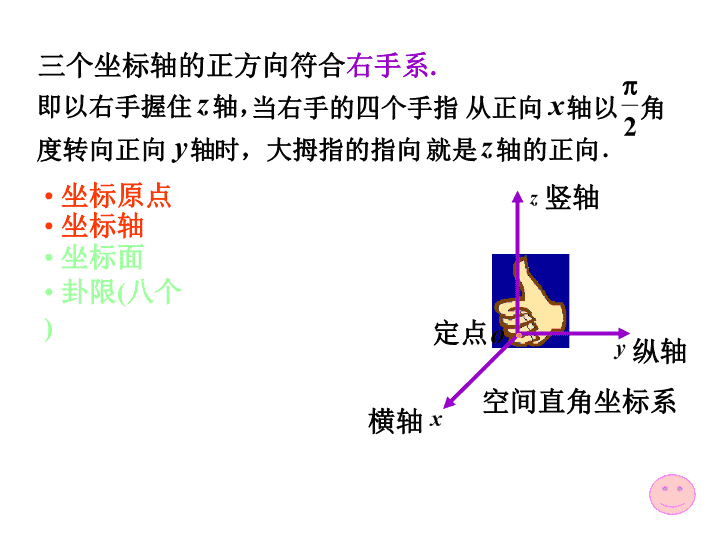
第二节点的坐标与向量的坐标1.空间直角坐标系3.向量的模，两点间距离5.向量的投影4.向量的方向角与方向余弦2.利用坐标作向量的线性运算\n一、空间直角坐标系由三条两两互相垂直的数轴按右手规则组成一个空间直角坐标系.过空间一定点O,横轴纵轴竖轴定点空间直角坐标系\n三个坐标轴的正方向符合右手系.即以右手握住z轴，当右手的四个手指从正向x轴以2p角度转向正向y轴时，大拇指的指向就是z轴的正向.横轴纵轴竖轴定点坐标原点坐标轴坐标面卦限(八个)空间直角坐标系\n坐标原点坐标轴坐标面卦限(八个)面面面\nⅦ面三个坐标面把空间分成八个部分----卦限ⅠⅡⅢⅣⅤⅥⅧ坐标原点坐标轴坐标面卦限(八个)面面\n向量点M有序数组(称为点M的坐标,也称为向量的坐标)向量称为点M关于原点O的向径。点M与向量的坐标相同。空间直角坐标系中有一点点M\n坐标轴上的点P,Q,R;坐标面上的点A,B,C原点O(0,0,0);特殊点的坐标:\n坐标轴:坐标面:\n向径点M有序数组(称为点M的坐标,称为向量的坐标)向量称为M原点O的向经。点M与向量的坐标相同。\n向量的坐标表示在空间直角坐标系下,设点M则的坐标为任意向量r可用向径OM表示.坐标x,y,z称为向量r在三个坐标轴上的分量向量xi,yj,zk称为向量r在三个坐标轴上的分向量\n二、利用坐标作向量的线性运算向量的加,减,数乘运算只需对向量的各个坐标分别进行相应运算！即有\n平行向量对应坐标成比例:\n例1解:\n例2.已知两点在AB直线上求一点M,使解:设M的坐标为如图所示及实数得即\n说明:由得定比分点公式:点M为AB的中点,于是\n三、向量的模，两点间距离公式\n因对两点与\n例3.求证以证:即为等腰三角形.的三角形是等腰三角形.为顶点\n解设P点坐标为所求点为例4在z轴上求与点A(-4,1,7)和点B(3,5,-2)等距离的点\n解例5已知两点A(4,0,5)和B(7,1,3)，求方向和AB相同的单位向量。\n四、向量的方向角与方向余弦与三坐标轴的夹角,,为其方向角.方向角的余弦称为其方向余弦.\n方向余弦的性质:\n例6.已知两点和的模、方向余弦和方向角.解:计算向量\n例7.设点A位于第一卦限,解:已知角依次为求点A的坐标.则因点A在第一卦限,故于是故点A的坐标为向径OA与x轴y轴的夹\n称为向量在轴u上的分向量.设,则数称为向量在轴u上的投影（或分量）记作五向量的投影\n是向量在轴上的投影是向量在轴上的投影是向量在轴上的投影对向量的投影与向量的坐标两个概念不加区分.\n关于向量投影具有与坐标相同的的性质：性质1其中为与轴的夹角.性质2性质3\n例8.设立方体的一条对角线为OM，一条棱为OA解:返回目录\n1.空间直角坐标系3.向量的模，两点间距离5.向量的投影4.向量的方向角与方向余弦2.利用坐标作向量的线性运算\n\n