大学物理 导体 24页

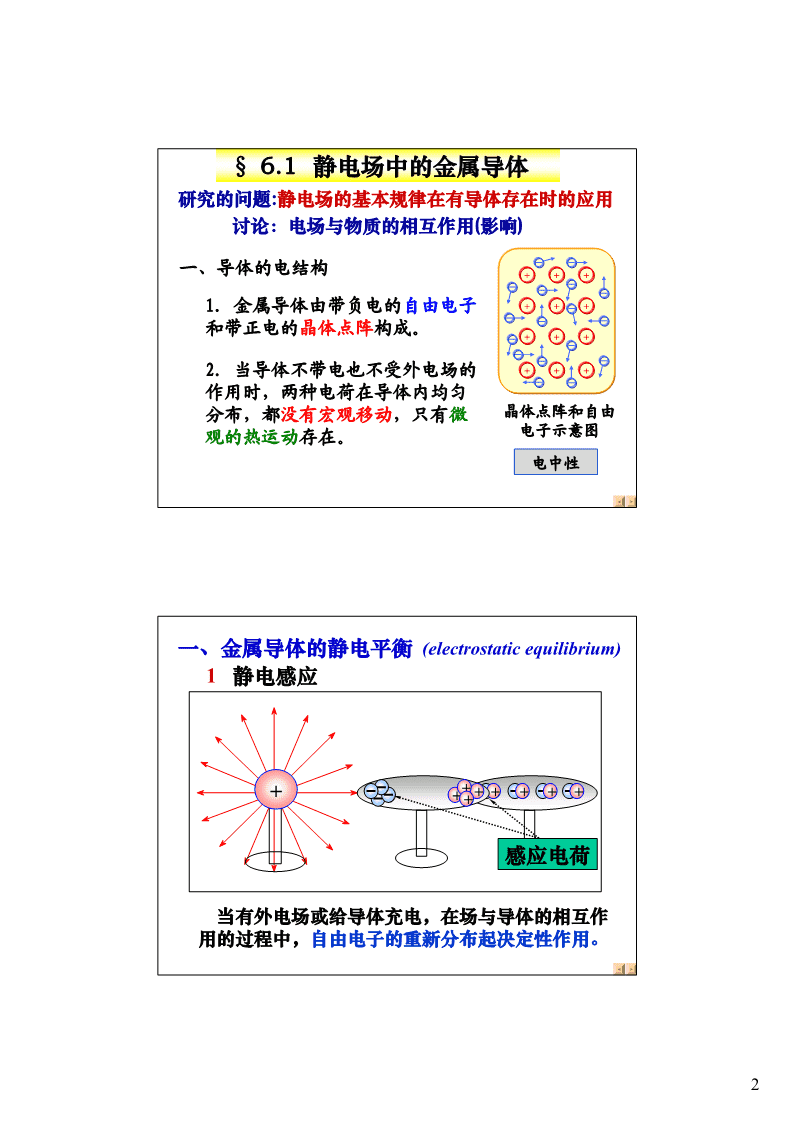
主要内容§1    静电场中的导体§2    电容和电容器§3    静电场中的电介质§4    带电体系的静电能1\n§6.1静电场中的金属导体研究的问题:静电场的基本规律在有导体存在时的应用讨论：电场与物质的相互作用(影响)一、导体的电结构+++1.金属导体由带负电的自由电子+++和带正电的晶体点阵构成。+++2.当导体不带电也不受外电场的+++作用时，两种电荷在导体内均匀分布，都没有宏观移动，只有微晶体点阵和自由观的热运动存在。电子示意图电中性一、金属导体的静电平衡(electrostaticequilibrium)1静电感应++++++++++感应电荷当有外电场或给导体充电，在场与导体的相互作用的过程中，自由电子的重新分布起决定性作用。2\n当把导体放入静电场E0中，导体中的自由电子在外电场E0的作用下定向运动，并在导体一侧集结出现负电荷，而另一侧出现正电荷，称静电感应现象。集结的电荷称为感应电荷。K'外电场与自由电荷移动后的附加场E之和为总场强KKKKK'E0EE=+EEoK0E'KE=0导体的静电平衡条件：KKK时,导体处于静电平衡状态！!'E内=Eo+E内=0此时导体内部和表面都无电荷定向运动！静电平衡条件：（1）导体内部任何一点处的电场强度为零；（2）导体表面处的电场强度的方向，都与导体表面垂直。反证法，若电场强度不为零，则自由电荷将能移动。3\n推论：导体为等势体，导体的表面是等势面。¾导体内部电势相等KK∵E=0enK()bGGE∴Ua−Ub=∫E⋅dl=0K()adlKe+++τ¾导体表面是等势面+A+KKB∵E⊥dl+KK∴UAB=∫ABE⋅dl=0导体等势是导体体内电场强度处静电平衡条件的处为零的必然结果另一种表述二静电平衡时导体上电荷的分布由导体的静电平衡条件和静电场的基本性质，可以得出导体上的电荷分布。1实心导体K∵E=0高斯面KKq++v∫ES⋅==d0++Sε+S+0+++∴q=0+结论：导体内部无净电荷，电荷只分布在导体表面.4\n2空腔导体空腔内无电荷时高斯KK面∫E⋅dS=0∑qi=0Si内表面？S电荷分布在表面外表面？若内表面带电，必等量异号高斯面KK∑qi∫E⋅dS==0Sε0++KK+＋+U=E⋅dl≠0+A－S+AB∫+BAB+++与导体是等势体矛盾结论：空腔内无电荷时，电荷分布在外表面,内表面无电荷.空腔内有电荷时高斯面KKq∫SE⋅dS=0+qS-q∑qi=0结论:空腔内有电荷+q时，空腔内表面有感应电荷-q，外表面有感应电荷+q．5\n导体空腔处于静电平衡时若腔内无带电若腔内有电荷q，则内体，电荷只能分表面上电量为-q，外布在外表面上；表面上电量为Q+q，Q为导体空腔原有电量。QQ+qSqS-q3导体表面附近场强与电荷面密度的关系作扁圆柱形高斯面n^KK：外法线方向∫E⋅dS=EΔS=σΔS/ε0ΔSSσ++++σ+KE=+E=0+ε0Gσ写作E=n^表ε0由于电场线与等势面垂直，因此导体表面附近的电场强度处处与表面垂直。6\n静电平衡条件：(充要条件)导体内部场强处处为零G电场E=0内导体表面邻近处场强垂直于导体表面GGσE⊥dSE=表面ε0导体为一等势体U=常量电势导体表面是一个等势面4.孤立带电导体表面电荷分布1).实验表明：孤立导体处于静电平衡时，它的表面各处的面电荷密度与各处表面的曲率有关：σ++++E=σ↑E↑;σ↓,E↓++++ε+++++0a.在表面凸出的尖锐部分(曲率是正值孤立导体且较大)电荷面密度较大，b.在比较平坦部分(曲率较小)电荷面密度较小，c.在表面凹进部分带电面密度最小。2).孤立的球形带电导体，球面上各部分的曲率相同，故电荷均匀分布，即面电荷密度在球面上处处相同。7\n尖端放电现象带电导体尖端附近的电场特别大，可使尖端附近的空气发生电离而成为导体产生放电现象．带电导体尖端附近电场最强σ↑E↑<电风实验>金属针上的电荷形成的“电风”会将蜡烛的火焰吹向一边，这就是尖端放电现象。++++++++++“电风”吹蜡烛8\n避雷针的工作原理+++++带电云－－－－－－接闪杆++静电感应电晕放电可靠接地为避免漏电危险，高电压的零部件必需做得十分光滑或成球面,相反,避雷针利用其尖端的电场强度大，空气被电离，形成放电通道。雷击尖端9\n空气中的直流高压放电图片：云层和大地间的闪电遭雷击后的草地云层和大地之间快速连续放电的结果：长3公里的中等闪电散发的热量等于200亿焦耳，温度可达摄氏1.5万度。10\nZ形通道被迫冲向云层俘获闪电：激光束引起空气电离，使闪电改道三、空腔导体第一类空腔（金属空腔导体,内部无带电体）(无论空腔导体是否带电、是否处于外电场中，)空腔导体都具有下列性质：1.内表面上不存在净电荷，所有净电荷都只分布在外表面。2.空腔内部电场强度为零，即它们是等电势。GG结论:在腔内E壳外表面+E壳外=0电量带电体这是静电屏蔽的一种基本含义。11\n2第二类空腔（金属空腔导体内部有带电体）1.空腔内表面有感应电荷。q–q内表面所带总电量与空腔内带电体的电量相等、符号相反。导体空腔是等势体，腔内场强不为零，电势不相等。U≠=CU=C11Q+q2.空腔外表面上的感应电荷的电量与内表面上的电量之和，要遵守电荷守恒定律。3.空腔外表面上的电荷分布与腔内带电体的位置无关，只取决于导体外表面的形状。腔内电荷q与内表面的感应电荷-q,对外部场的贡献恒为零。4.空腔导体接地时，外表面上的感应电荷被大地电荷中和，所以不带电荷。金属空腔是零等势体。此时壳内的任何电场都不影响外界，也不受外界影响。U=05.若第二类空腔导体接地，并且腔外有带电体时，外表面上的感应电荷被大地电荷部分中和，所Q'q–q+带电荷的多少必须保证腔内、腔内表面、腔外表面以及腔外电荷在导体内产生的场强为零，即满足静电平衡条件。金属空腔是零电势。接地：意味着“导体电势为零”，Q+q’U=0不意味着“电荷一定全跑光”。12\n腔外表面的电荷分布不影响外界KE=0不影响腔内电场分布不接地但是腔内有无电荷对腔外有影响。U=0外界不影响内部例如高压设备都用金属导体壳接地做保护，它起静电屏蔽作用，内外互不影响。例如在电子仪器、或传输微弱信号的导线中都常用金属壳或金属网作静电屏蔽。或常把测量仪器或整个实验室用金属壳或金属网罩起来，使测量免受外部电场的影响。空腔导体的静电屏蔽原理：空腔导体(无论接地与否)将使腔内空间不受外电场的影响，而接地空腔导体将使外部空间不受空腔内的电场的影响.四、有导体存在时静电场的计算1.静电平衡的条件E=0U=C内原GG1∫E⋅ds=∑Qi高斯定理Sε2.基本性质方程0iGG∫E⋅dl=0环路定理则L∑Qi=常量.3.电荷守恒定律iG有导体存在时的E,U分布求解思路：先假设导体表面的电荷面密度σ，再由导体静电平衡条件，用叠加原理与库仑定律或高斯定理与环路定理求出σG静电平衡条件导体上的计算E,U分电荷守恒定律布（方法同前）电荷分布13\nB例1:已知：金属球A与金属球壳B同心放置，QA球A的半径为R1、带电为q；金属球壳B的内q外半径分别为RR带电为Q；求:(1)电量分o2、3布（2）场强分布；(3)球A和球壳B的电势R3R2R1解：1)导体带电在表面∴球A表面均匀分布着电量q,Q+qB−q相当于一个均匀带电的球面Aqo由高斯定理和电量守恒可以证明壳B的电量分布R3R2R1Q=−qB内相当于均匀带电的球面Q=Q+qB外（2）场强分布Q+qE1=0(rRB4234πεr014\n（3)球的电势分布∞∞GG()rR<1U1球A=∫∫rrE⋅dl=EdrR1R2R3∞=Edr+Edr+Edr+Edr∫r1∫R12∫R23∫R34Eqq11+Q=+0()−++044πεRRRπε01203r1qqq+Q=(−+)4πεRRR0123R2R3∞()RrR12≤≤U2=∫rE2dr+∫RE3dr+∫RE4dr23q11q+Q=(−)+0+4πεrR4πεR0203(3)球壳B的电势()R≤rR≤23R3∞Q+qUE=+drEdr334C∫∫rR3−qqQ+RqRAB=+0314πεRR032qQ+=U4πεR03∞()rR>UE=dr344∫rrqQ+=4πεr015\n又解（3)球A的电势qqRU=11等效:在真空中三个4πεR01均匀带电的球面−q−qU=24πεR02Rq+Q2U=34πεRQ+q03根据叠加原理Rq−qQ+q3U=++球A4πεR4πεR4πεR010203球壳B的电势qR1qU1=−q4πεr0−qq+QU=U=R22壳4πεr04πε0R3q+QQ+qU=34πεR03rR316\n例2:接地导体球附近有一点电荷,如图所示。求:导体上感应电荷的电量解:接地即U=0设:感应电量为QlR由导体是个等势体oqo点的电势为0则QqR+=0Q=−q4πε0R4πε0ll例3：两块导体平板平行并相对放置，所带电量分别为Q和Q′，如果两块导体板的面积都是S，且视为无限大平板，试求这四个面上的面电荷密度。'解：设四个面的面电荷密度分别为σ、QQ1σ2、σ3和σ4，空间任一点的场强都是由四个面的电荷共同提供的。由高斯定σσσσ1234理，各面上的电荷所提供的场强都是σi/2ε0。另外，由于导体内部的合成场强为EEAB零。若取向右为正方向，则处于导体内部的点A和点B的场强可以表示为Pσσσσ12341E=(σ−σ−σ−σ)=0A12342ε01EE=(σ+σ+σ−σ)=0B1234E2ε0E4E17\n各个分区的电场分布（电场方向以向右为正）：σσσσ在Ⅰ区：1234E=−−−−方向向左Ι2222εεεε0000σσσσ在Ⅱ区：E=+−−1234方向向右ΙΙ2222εεεε0000σ1σ2σ3σ4σ1σ2σ3σ4σ1σ2σ3σ4E1E1E1E2E2E2E3E3E3E4在Ⅲ区：E4E4P•P••P根据已知条件σσσσ1234S(σ1+σ2)=QS(σ3+σ4)=Q′.S可解得(Q+Q′)σ=σ=142S(Q−Q′)Eσ2=−σ3=Q'2SQ上式表明两块无限大的导体平板，内侧表面上面电荷密度大小相等、符号相反。如果Q=−Q′，可以求出：Qσσ==0,σσ=−=1423S18\n例4:两个无限大带电平面，面积为S，带电量Q的一个金属板，与另一不代电的金属平板平行放置。求:静电平衡时，板上电荷分布及周围电场分布.σσσσS1234ABSKKE=?KE=?E=?QEIEIIEIIIQ解：设静电平衡后，金属板各面所带设Q>0电荷面密度如图所示(σ+σ)S=Q12由已知条件：σ+σ=034由静电平衡条件和高斯定理，做如图所示高斯柱面可得：GG选一个两底分别在两个金属∫E⋅dS=0板内而侧面垂直于板面的封闭曲面作为高斯面。∑qi=0σ+σ=0σσσσ231234金属B板内任一点的场强S为零，由叠加原理得：σ1σ2σ3σ4即：++−=02εo2εo2εo2εoσ+σ+σ−σ=01234EIEEIIIII以上四个方程联立可求出：Q设Q>0σ=σ=QQQ122Sσ3=−σ4=2S2S19\n由各板上的电荷面密度、金属板内场强为零和高斯定理可得各区间的场强：σ=σ=QQQ122Sσ3=−σ4=2S2S设Q>0σσσσ1234QEI=方向向左2εSoQ方向向右E=II2εSoEIEIIEIIIQE=方向向右QIII2εSo§6-6电容和电容器R1.孤立导体的电容QC=电容是指导体储存电荷的能力。U升高单位电压所需的电量为该导体的电容。孤立导体是指附近无其它带电体或导体。例如：孤立导体球的电容1qU=4πεR单位1F1C/V=0−6q1μF10F=C==4πεR1pF10=−12F0U任何孤立导体，q/U与q、U均无关，定义为电容64−♦地球RC=×6.410m,≈×710FEE20\n2.电容器的电容电容器：两相互绝缘的导体组成的系统。是一储能元件。电容器的两极板常带等量异号电荷。几种常见电容器及其符号：纸质电容器陶瓷电容器电解电容器可变电容器钽电容器由两个导体组成的导体如图用导体空腔B把导体A包围起来，B以外的导体和电场都不会体系----电容器。影响导体A以及A、B之间的电场。电容器的电容定义为RBQQRAAC==＋QU−UU-QABAB注意：电容器的电容与导体的几何形状,排列的位置和其间的电介质有关，而与其所带电量和电位差无关。孤立导体的电容是其与无穷远处导体组成的电容器的电容。21\n♦电容器电容的计算K步1.设两极板分别带电±Q2.求E(高斯定理)BKK骤3.求，UUEAB=∫⋅dl4.求C，CQU=/A1.平行板电容器σQd(1)板间电场强度：E==εεS＋00＋＋QdS(2)两板间的电压：UE==d＋εS＋0＋U＋Qε0S＋(3)平行板电容：C==+σ−σUd＋2.圆柱形电容器（同轴电缆）设两导体圆柱面单位长度上分别带±λ的电荷。λ(1)E=<,(RrR<)122πεr0-+R2λdrQR2-+R(2)U==∫lnL1R122πεrLπεR-+001R-+2QR(3)柱形电容2CL==2lπεnUR0_1___+++_++RR21+dd+++若dRRR=−<<,ln=≈ln__211RRR111_2πεεlRS00AC≈=平行板电容器电容dd22\n3.球形电容器设内外球面上所带电荷量为±QQ＋(1)E=2er()RrR12<<＋＋4πε0rrR1QrR2d＋＋(2)UEl=⋅=dO∫lR∫2R4πε01r＋2＋Q11＋ε=−()r4πεRR012Q4πεRR(3)球形电容012C==URR−21R2→∞CR=4πε0孤立导体球电容4、电容器的串联与并联等效电容•串联+Q-Q+Q-Q+Q-QóóóóóUAC1UBC2UCUACUCQQU−U=ABU−U=CAC1CQ+）UB−UC=111C2=+⎛11⎞CC1C2U−U=Q⎜+⎟AC⎜⎟⎝C1C2⎠1n1一般n个电容器串联=∑的等效电容为CiCi串联时总电容比每个电容器都减小了。若增强耐压，可将多个电容串联例如1atm下的干燥空气的击穿强度为3kV/mm.23\n+Q1-Q1等效电容•并联óóC1óóUA+Q2-Q2UBUCUABQC2C=1Q1C=U−UABQ=C()U−UU−U11ABAB+）Q2=C2()UA−UBQ=C(UA−UB)Q1+Q2=()C1+C2(UA−UB)C=C1+C2一般n个电容器并联的等效电容为并联时总电容增大实际的电容器的性能主要指标n常用电容：100μF25VC=∑Ci当单独一个电容器的电容或i耐压能力不能满足要求时。例1：两半径为R的平行长直导线中心间距为d，且，dR>>，求单位长度的电容。解：设两金属线的电荷线密度为±λ2RλλEEE=+=+E+−+λ−λ22πεxdπε()−x00dR−−λdR11PUE==∫∫d(x+)dxOxRR2πεxdx−xd−x0λλdR−dE=≈lnln+πε00RπεRE−λd单位长度的电容C==πεlnd0UR24