大学物理 (37) 193页

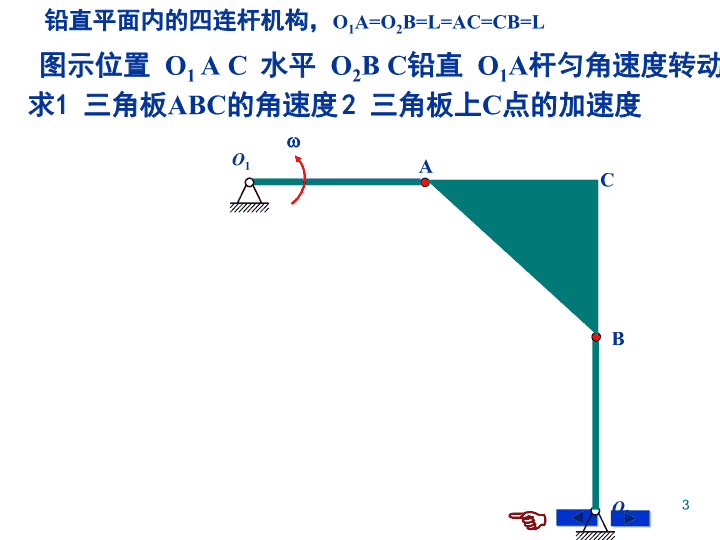
作业1铅直平面内的运动机构。定滑轮A动滑轮B的质量m半径R，可看成均质圆盘；物块D的质量为2mDABv求：图示瞬时系统的动能。已知图示瞬时物块D向下运动的速度v。绳的质量不计,绳与轮间无相对滑动。作业2习题12-12作业3习题12-141\n关于期末考试的有关事宜比例：平日成绩10%；卷面成绩90%重点章节静力学平面任意力系运动学点的合成运动速度加速度合成定理平面运动速度（角速度）加速度（角加速度）的问题动力学动力学普遍定理的单独应用动力学普遍定理综合应用题目类型：简单计算题选择题计算题动力学基本量的计算2\n铅直平面内的四连杆机构，O1A=O2B=L=AC=CB=L图示位置O1AC水平O2BC铅直O1A杆匀角速度转动求1三角板ABC的角速度2三角板上C点的加速度O2wO1ABC3\n均质圆柱体A和B质量均为m，半径均为R。圆柱A可绕固定轴O转动。一绳绕在圆柱A上，绳的另一端绕在圆柱B上。求B下落时，B的质心C点的加速度。不计摩擦和绳的质量。注意：截止到今天还没有学到一个万能的微分方程能够解决刚体系统中，已知力求运动的问题！！ABC问题的提出4\n5\nDCABE问题的提出更为复杂的运动机构求物块D向下运动的加速度思考利用所学的知识如何解决该问题？从两处断开，分别列运动微分方程？有没有更好的方法？？？6\n第十二章动能定理7\n本章重点★★★2动能定理★★★★★1两个重要概念力的功动能★★★★3动力学普遍定理的综合应用★★★8\n§12－1力的功要求1力的功的表达式（理解记牢）本章的第一个重点概念2力的功的计算(重点掌握)9\n2变力功的计算（1）自然表达式F（+）§12－1力的功1力的功是代数量恩格斯说功是从量的方面看的运动形式的变化！！适用于轨迹已知的情况下！！变力功的计算—元功表达式10\nF（2）矢量表达式§12－1力的功o最一般表达式推导公式2变力功的计算—元功表达式受力物体上的作用点的微小位移11\nF§12－1力的功（3）直角坐标表达式xyzOjik力可以正交分解时使用变力功的计算—元功表达式12\n几种常见力的功1）重力的功2）弹性力的功3）定轴转动刚体上力的功（力偶的功）§12－1力的功13\n3）作用于定轴转动刚体上的力的功刚体转过微小角位移后力所作的功z？另外两个力呢？力的特点：变力，且力作用点的轨迹是曲线（圆周运动）§12－1力的功3几种常见力功的计算14\n当力对轴之矩（力偶矩）为常量时：注意：正功负功如何判断？二几种常见力功的计算作用于定轴转动刚体上的力的功§12－1力的功15\n阻力偶矩（M以N.m计，以rad计），例题OMM’圆盘可绕水平轴O转动。在盘上作用一主动力偶，力偶矩按M=4的规律变化，求:由=0到时，力偶的功。正功还是负功？？变力偶的功功如何计算？常力偶的功功如何计算？16\n作业1铅直平面内的运动机构。定滑轮A动滑轮B的质量m半径R，可看成均质圆盘；物块D的质量为2mDABv求：图示瞬时系统的动能。已知图示瞬时物块D向下运动的速度v。绳的质量不计,绳与轮间无相对滑动。作业2习题12-1217\n思考题1摩擦力是否一定作负功？静滑动摩擦力可以作正功。！！思考题2半径为R，沿直线路面纯滚动的车轮。地面给车轮的摩擦力是静滑动摩擦力还是动滑动摩擦力？当在主动力偶作用下，轮心向右移动的距离为S时。静滑动摩擦力的功等于？结论：当圆轮沿固定面作纯滚动时，圆轮受到的摩擦力一定是静滑动摩擦力，且静滑动摩擦力的功一定等于零。1受力物体上的作用点的微小位移两种处理方法：2将静摩擦力用力的平移定理平移到质心上18\n计算轮心向右移动的距离为S时，力F对盘所作的功1受力物体上的作用点的微小位移均质圆盘质量为m、半径为R，其外圆上缠绕很多圈无重细绳，F绳头上用常力F作用，使盘沿水平直线路面纯滚动两种处理方法：2将力F用力的平移定理平移到质心上19\n正功还是负功？如何计算？根据常力偶的功的计算方法进行计算。结论：当圆轮沿固定面作纯滚动时，圆轮受到的摩擦力一定是静摩擦力，思考题3当轮心向右移动的距离为S时。滚动摩阻力偶的功？滚动摩阻力偶作负功且静摩擦力的功一定等于零。半径为R，沿直线路面纯滚动转角如何计算？20\n判断题判断下列说法是否正确？1功是非负的标量2质点作曲线运动时，作用在质点上的切向力作功，法向力不作功。3切向力永远作正功。4圆盘在粗糙面上作纯滚动。1）由于静摩擦力作用点是圆盘的瞬心点，因此静摩擦力的功等于零。2）由于圆盘运动，而静摩擦力不等于零，其位移也不等于零，因此静摩擦力作功。21\n§12－2质点和质点系的动能要求：熟练掌握刚体动能的计算本章的第二个重点概念预备知识1刚体对轴的转动惯量的计算2平移刚体的判断以及其上一点速度的计算3定轴转动刚体的判断以及转动角速度的计算4平面运动刚体的判断以及其角速度的计算22\n一质点的动能二质点系的动能§12－2质点和质点系的动能（一）一般表达式瞬时值，是机械运动的另一种度量形式。1平移刚体的动能（二）刚体的动能（重点要求熟练掌握）平移刚体的运动特点可以和哪个公式类比？23\n（二）刚体的动能（重点要求熟练掌握）2定轴转动刚体的动能可以和哪个公式类比？§12－2质点和质点系的动能z24\n3平面运动刚体的动能JP＝JC+md2思考dw=什么?dwCP为什么可以用这个公式？？思考问题1：将上述公式改为对任意点是否可以？思考问题2：如何选择上述两个公式？§12－2质点和质点系的动能（二）刚体的动能（重点要求熟练掌握）25\n总结1计算刚体的动能和计算刚体的动量矩相类似，2平移刚体的动能定轴转动刚体的动能平面运动刚体的动能3对刚体系统而言凡是有质量又运动的物体必然有动能4要用绝对的速度（角速度）§12－2质点和质点系的动能必须要分析刚体的运动形式！26\n例题1均质圆盘质量m，半径r,可绕轴O转动，转动的角速度已知。求：图示瞬时圆盘的动能。AO均质杆质量m长度为L图示瞬时转动的角速度为已知求：图示瞬时杆的动能。OCw均质偏心凸轮质量m偏心距为e图示瞬时转动的角速度为已知求：图示瞬时圆盘的动能。本质！！27\n例题2均质圆盘质量m，半径r,可绕轴O转动，角速度为w.求：图示瞬时系统的动能其上缠有一质量不计的绳，重物A的质量为m，并设绳与圆盘间无相对滑动。28\nCv例题3均质圆盘质量为m半径为R，沿水平直线路面作纯滚动。思考问题1圆盘的运动形式？思考问题2选择公式的形式？结论：平面运动刚体若能找到瞬心用那个公式计算动能！图示瞬时，轮心的速度为v.求该瞬时盘的动能。v均质圆盘质量为m半径为R，由不计质量的绳挂在固定的墙上。图示瞬时，轮心的速度为v.求：该瞬时盘的动能。29\n例题4铅直平面内的均质杆质量为m，长为L，在铅直平面内B端沿着水平地面，A端沿着铅垂墙壁运动。ABv思考问题1AB的运动形式？思考问题2选择公式的形式？结论：平面运动刚体若能找到瞬心设AB与水平面成夹角时B端的速度为v。求:该瞬时杆的动能PAB30\n例题5铅直平面内的运动机构。定滑轮A动滑轮B的质量m半径R，可看成均质圆盘；物块D的质量为2m、E的质量为m。思考问题1系统由几部分组成？DCABEv求：图示瞬时系统的动能已知图示瞬时物块D向下运动的速度v。绳的质量不计,绳与轮间无相对滑动。每一部分的运动形式如何？思考问题2动滑轮B的动能如何计算？31\n动量和动能都是机械运动形式的度量。动量是矢量有方向动能是标量与方向无关§12－2质点和质点系的动能思考问题3若物块D是放在与水平面成一倾角固定的斜面上其他条件都不发生改变，系统的动能是否发生改变？CABEv为什么？？DCABEv32\n★★★§12－3动能定理★★本章的第二个重点问题1质点系动能定理的内容特点(记牢理解)2质点系动能定理的应用（重点掌握）要求：能够解决什么问题？如何解决？预备知识1力的功的计算2质点系动能的计算（刚体动能）33\n一、质点的动能定理（基础）§12－3动能定理质点动能的增量等于作用于质点上力所作的元功在一段路程中，质点动能的改变量等于作用于质点上力在路程上所作的功。34\n二、质点系的动能定理2积分形式质点系动能定理微分形式质点系动能定理积分形式1微分形式§12－3动能定理35\n探索系统全部力的功的问题固定铰支座其约束力也不作功。全部力外力内力主动力外部约束力理想光滑面约束，约束力的功等于零。当轮沿固定面作纯滚动时，摩擦力是静摩擦力为什么？为什么？BAORAOB为什么？静摩擦力的功等于零。滚阻力偶作负功36\n3探索全部力的功的问题全部力外力内力主动力外部约束力思考：内力的主矢以及对任一点的主矩矢恒等于零。变形元件（弹簧）发动机内力作功内力所作的功（和）是否一定恒等于零？刚体所有内力作功的和等于零。为什么？§12－3动能定理人骑自行车时人和车组成的系统而言内力作功人运动时内力做功37\n3探索全部力的功的问题全部力外力内力主动力外部约束力刚体所有内力作功的和等于零。为什么？AOBAODrR不可伸长的绳----刚体38\n总结全部力的功1理想约束----约束力的功（的和）等于零的约束2外部约束里的理想约束理想光滑面约束固定铰支座当轮沿固定面作纯滚动，不计滚阻力偶时3内部约束里的理想约束光滑铰链刚性二力杆及不可伸长的细绳刚体所有内力39\n三（质点系）动能定理的特点1标量方程----只能求解一个未知量2不考虑中间过程，对运动不加限制3可以解决什么问题？思考能否求出理想约束里面的外部约束力？能否求出理想约束里面的内部约束力？对于具有理想约束的刚体运动机构，若在主动力（力矩）的作用下运动（隐含运动）。求运动量（速度角速度）、加速度（角加速度）§12－3动能定理AOB40\n四应用1取系统为研究对象，分析受力，选积分形式2计算始、末位置系统的动能注意：动能计算应该注意的问题3计算全部力的功4代入公式并求解★★注意内力的功外部约束力的功主动力的功★★§12－3动能定理理想约束则约束力的功(和)为零41\nOA例题1铅直平面内的均质杆OA质量m杆长L。A端系一质量不计的细绳，静止在水平位置。转动刚体几个自由度？某瞬时将绳剪断。求杆与水平位置成夹角时杆的角速度、角加速度。1取系统为研究对象，分析受力，选积分形式2计算始、末位置系统的动能3计算全部力的功单个刚体显示不出动能定理的优越性4代入公式并求解动能定理的优越性表现在一个自由度的刚体系统中。42\n例题2物块A的质量为m1，系在质量不计的不可伸长的绳子上，绳子跨过质量不计的定滑轮D，并绕在鼓轮上。动能功分别表示成哪个物体的量的函数？请同学们作笔记时留下空隙，该例题综合应用时用！全部力的功？几个自由度？由于物块A下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R，r对质心轴O的回转半径为。不计滚动阻力偶。求：重物A由静止开始下降距离为S时的速度、加速度。AODrR43\n作业1P28611-25仅求杆AB的加速度用动能定理解决作业2P321习题12-12注意：系统位于水平面内作业3（选）P327综-21仅求O点的加速度杆OA始终与斜面平行44\n关于16周周六的补课问题时间：16周周四一二节地点：五号教学楼102教室时间：16周周四一二节地点：五号教学楼102教室45\n判断题1有条件作平面运动刚体，如果所受外力主矢恒等于零，2有条件平面运动刚体，如果所受外力对质心的主矩恒则刚体的运动形式只能是绕质心的转动。则刚体的运动形式只能是平移。等于零要看运动的初始条件！！要看运动的初始条件！！质心是否运动？？是否有转动的角速度？？46\n物块A的质量为m1，系在质量不计的不可伸长的绳子上，绳子跨过质量不计的定滑轮D，并绕在鼓轮上。由于物块A下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R，r对质心轴O的回转半径为。不计滚动阻力偶。求：重物A下降的加速度AODrR这两段绳的张力相等有无条件？补充方程如何建立？？简单方法！用动能定理求解更简单！！47\n全部力的功知识点回顾动能定理的内容外力内力主动力外部约束力理想约束主动力的功48\nOA例题1铅直平面内的均质杆OA质量m杆长L。A端系一质量不计的细绳，静止在水平位置。转动刚体几个自由度？某瞬时将绳剪断。求杆与水平位置成夹角时杆的角速度、角加速度。1取系统为研究对象，分析受力，选积分形式2计算始、末位置系统的动能3计算全部力的功单个刚体显示不出动能定理的优越性4代入公式并求解动能定理的优越性表现在一个自由度的刚体系统中。49\n例题2物块A的质量为m1，系在质量不计的不可伸长的绳子上，绳子跨过质量不计的定滑轮D，并绕在鼓轮上。动能功分别表示成哪个物体的量的函数？请同学们作笔记时留下空隙，该例题综合应用时用！全部力的功？几个自由度？由于物块A下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R，r对质心轴O的回转半径为。不计滚动阻力偶。求：重物A由静止开始下降距离为S时的速度、加速度。AODrR50\n3动能定理的优越性对于具有理想约束的复杂一个自由度的刚体运动机构，求运动量（速度角速度）、加速度（角加速度）若在主动力（力矩）的作用下运动（隐含运动）。2动能定理的特点1）标量方程----只能求解一个未知量2）不考虑中间过程，对运动不加限制知识点回顾51\n思考：如果计入定滑轮的质量m3，半径为r可以看成均质圆轮。其他各项都不发生改变。全部力的功始末位置的动能如何计算?请同学们记笔记时留下空隙综合应用时用！自己动手，一切都有！！首先想到了运动机构的复杂性！动能定理的独特性！求：重物A由静止开始下降距离为S时的速度、加速度。AODrR质量不计的不可伸长的绳子物块Am1鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R，r对质心轴O的回转半径为。不计滚动阻力偶。52\n作业1综合题-13P325将杆KC去掉，C处加上固定铰链支座。求1）物块A上升的加速度求2）HE段绳的张力作业2综合题-14求：鼓轮的角加速度和绳子的张力以及斜面对圆柱体的摩擦力？不求轴承的水平约束力53\n关于18周周三补课问题时间：18周周三三四节地点：三号教学楼205教室时间：18周周三三四节地点：三号教学楼205教室54\n3动能定理的优越性对于具有理想约束的复杂一个自由度的刚体运动机构，求运动量（速度角速度）、加速度（角加速度）若在主动力（力矩）的作用下运动（隐含运动）。回顾1动能定理的内容2动能定理的特点1）标量方程----只能求解一个未知量2）不考虑中间过程，对运动不加限制55\n练习如图，铅直面内均质杆质量为m，长为L，可绕距上端点L/3的转轴O转动，jCO求杆由水平位置静止开始转动到任一位置时杆的角速度和角加速度56\nDCABE请同学们留下空隙综合应用时用！例题3铅直平面内的运动机构。定滑轮A动滑轮B的质量m、半径R，可看成均质圆盘；首先想到了运动机构的复杂性！动能定理的独特性！动能功分别表示为物块D质量均为2m，E的质量m，绳的质量不计。绳与轮不打滑。开始静止，求物块D向下运动S时的速度和加速度。哪个物体的量的函数？全部力的功！始末位置的动能？？57\n例4重物A和B通过动滑轮D和定滑轮而运动。设重物A和B的质量均为m，滑轮D和C的质量均为M，且为均质圆盘。重物B与水平面间的动摩擦系数为f'，绳索不能伸长，其质量忽略不计。如果重物A开始时向下的速度为v0，试问重物A下落多大距离，其速度增大一倍。DABCv058\n2v0DABCv0系统动能59\n受力分析DABCmgMgMgmgFNFSFOyFOx60\n3动能定理的优越性对于具有理想约束的复杂一个自由度的刚体运动机构，求运动量（速度角速度）、加速度（角加速度）若在主动力（力矩）的作用下运动（隐含运动）。收获1动能定理的内容2动能定理的特点1）标量方程----只能求解一个未知量2）不考虑中间过程，对运动不加限制61\n动能定理是万能的吗？不能求理想约束里面的外部约束力不能求理想约束里面内部约束力OA铅直平面内的均质杆OA质量m杆长L。A端系一质量不计的细绳，静止在水平位置。某瞬时将绳剪断。求该瞬时杆的角加速度用那个定理就可以立即解决？？定轴转动微分方程62\n§12－4功率功率方程要求理解功率计算公式一功率1定义单位时间力的功P2功率计算公式二功率方程非重点的内容有用功的功率无用功的功率63\n§12－5势力场、势能、机械能守恒定律要求掌握机械能守恒定律的适用条件非重点的内容（课下自学）64\n§12－5势力场、势能、机械能守恒定律一、势力场2力场3势力场4保守力：势力场内对应的场力。完全由所在位置确定的力的作用，此空间称为力场。场力作功只决定于力作用点的始末位置，1场：质点在某空间内的任何位置都受到一个大小和方向而与路径无关的力场。65\n二、势能势能：注意定义§12－5势力场、势能、机械能守恒定律三、机械能守恒定律●机械能—系统所具有的动能与势能的代数和●保守系统—仅在有势力作用下的系统。●机械能守恒—系统仅有有势力作功时，其机械能保持恒定。势力场中选定势能零点66\n练习两个67\n全部力的功内容回顾动能定理的内容外力内力主动力外部约束力理想约束主动力的功68\n一动力学普遍定理（一）内容一定要牢记（二）基本量一定要会计算动量计算动能动量矩都涉及到转动惯量的问题转动惯量计算的几种情况平行移轴定理已知回转半径P271前三种简单几何形状的物体对质心轴的转动惯量必须牢记动量矩动能力的功69\n§12－6普遍定理综合应用本章的第三个重点问题一动力学普遍定理动量定理P24810-11P25210-14动量矩定理P26111-10P26411-11P27611-25动能定理P29612-19各自的守恒定理以及守恒条件难点70\n一动力学普遍定理（三）各定理的特点以及能够解决的问题1动量定理若左侧已知（运动的加速度量）可以求运动过程中的系统的外部约束力能够解决什么样的问题？ABO均质圆盘质量为m1，A质量为m2B质量为m3绳质量不计，盘顺时针加速转动。图示瞬时的角加速度为已知求轴承O处的约束力。对系统而言的外部约束力71\n一动力学普遍定理（三）各定理的特点以及能够解决的问题2动量矩定理的系列定理在综合应用中一般用于运动量已知，求运动过程中的内部约束力。能够解决什么样的问题？DCABE求定滑轮A与动滑轮B之间的那段绳的张力若定滑轮转动的角加速度已知、逆时针ABO单独应用时一般可以解决已知力求运动量的问题72\n（三）各定理的特点以及能够解决的问题一动力学普遍定理3动能定理能够解决什么样的问题？对于具有理想约束的复杂刚体运动机构，求运动量（速度角速度）、加速度（角加速度）AODrR若在主动力（力矩）的作用下运动（隐含运动）。73\n一动力学普遍定理（三）各定理的特点以及能够解决的问题已知运动量1动量定理2动量矩定理求内部约束力求外部约束力已知运动量3动能定理已知主动力（力矩）求运动量求运动过程中约束力？？二题目类型（一）求运动过程中的约束力74\n例题1如图，铅直面内均质杆质量为m，长为L，可绕距上端点L/3的转轴O转动，jCO首先想到哪个定理？运动量不知道怎么办？动能定理打先锋，解决运动过程中的运动量求杆由水平位置静止开始转动到任一位置时O处的约束反力。75\nBAOmgFOtFOn铅直面内均质杆质量为m，长为L，可绕距上端点L/3的转轴O转动，到任一位置时O处的约束反力。1动能定理解决运动量2动量定理（质心运动定理）解决外部约束力启发：76\n例题2物块A的质量为m1，系在质量不计的不可伸长的绳子上，绳子跨过质量不计的定滑轮D，并绕在鼓轮上。由于物块A下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R，r对质心轴O的回转半径为。不计滚动阻力偶。求：1物块A下降的加速度2定滑轮与鼓轮之间的那段绳的张力。首先想到的定理？选系统动能定理开路先锋，解决运动量AODrR77\n求系统的内约束力然后选动量矩定理的系列定理平面运动刚体启发AODrR有固定轴对瞬心（质心）固定轴的动量矩定理首先应用动能定理解决运动量运动分析运动分析鼓轮半径为R，r直线路面纯滚动78\n例题3P325综合题-12BACO要求的是系统的内部约束力首先想到的定理是？选系统以动能定理开路先锋，解决运动量求出滚子的轮心的加速度启发求内约束力时首先应用动能定理解决运动量不计滚阻力偶和轴承处的摩擦，不计绳的质量绳不可伸长绳与轮不打滑动能功分别表示成哪个物体的量的函数？始末位置的动能全部力的功动量矩定理的系列定理79\n求系统的内约束力时然后选动量矩定理的系列定理平面运动刚体收获对瞬心（质心）BACO有固定轴固定轴的动量矩定理首先应用动能定理解决运动量运动分析运动分析80\nDCABE例题4铅直平面内的运动机构。定滑轮A动滑轮B的质量m半径R，可看成均质圆盘；首先想到的定理是？选系统动能定理开路先锋，解决运动量动量矩定理的系列定理，求出内约束力即绳的张力物块D质量为m，E的质量m，绳的质量不计不可伸长求定滑轮A与动滑轮B之间的那段绳的张力绳与轮不打滑。81\n例题5物块A的质量为m1，系在质量不计的不可伸长的绳子上，绳子跨过质量m3，半径为r可以看成均质圆轮的定滑轮D，然后绕在鼓轮上。求外部约束力想到哪个定理？由于物块下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R、r对质心轴O的回转半径为。不计滚动阻力偶。求定滑轮D的轴承处的约束力。AODrR思考问题82\nA的质量为m1，质量m3，半径为r可以看成均质圆轮的定滑轮D，求外部约束力动量定理鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R、r对质心轴O的回转半径为。不计滚动阻力偶。求定滑轮D的轴承处的约束力。ADm1gm3gFxFyFT需要运动加速度量绳的张力83\nA的质量为m1，质量m3，半径为r可以看成均质圆轮的定滑轮D，动能定理开路先锋，解决运动量动量矩定理的系列定理，鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R、r对质心轴O的回转半径为。不计滚动阻力偶。求定滑轮D的轴承处的约束力。AODrR需要运动加速度量绳的张力求出绳的张力。84\nA的质量为m1，质量m3，半径为r可以看成均质圆轮的定滑轮D，求外部约束力动量定理鼓轮沿水平直线路面纯滚动。鼓轮的质量为m2,半径为R、r对质心轴O的回转半径为。不计滚动阻力偶。求定滑轮D的轴承处的约束力。ADm1gm3gFxFyFT85\nBACO不变化的是解决问题的思路！！假设二者的质量都为M,半径相等，均质盘，块C的质量为m,求辊子向下纯滚时中心的加速度动轮与定轮之间那段绳的张力粗糙斜面对辊子的摩擦力(沿斜面向上)作业86\n一动力学普遍定理（三）各定理的特点以及能够解决的问题已知运动1动量定理2动量矩定理求内部约束力。求外部约束力已知运动3动能定理已知主动力求运动量求运动过程中约束力？？87\n总结求一个自由度刚体系统运动过程中的约束力首先取系统为研究对象，用动能定理求出运动量若求内约束力若求外约束力AODrR考虑动量矩定理的系列定理一般选择动量定理（质心运动定理）88\n物块A的质量为m系在质量不计的不可伸长的绳子上，绳子跨过质量m半径为r可以看成均质圆轮的定滑轮D，3地面对鼓轮的摩擦力。注意此题可以有N多变化。1重物由静止开始运动，下降距离S时的加速度；2两段绳的张力；AODrR由于物块下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m,半径为R，r对质心轴C的回转半径为不计滚动阻力偶，绳子与轮之间不打滑。绳子位置的变化定滑轮处可以加主动力偶89\n综合题12P325可以求O处的约束力。思路BACO1动能定理解决运动的加速度量2动量矩定理的系列定理解决绳的张力3动量定理解决运动轴承处的约束力需要绳子的张力运动的加速度量90\n物块A的质量为m系在质量不计的不可伸长的绳子上，绳子跨过质量m半径为r可以看成均质圆轮的定滑轮D，3地面对鼓轮的摩擦力。注意此题可以有N多变化。1重物由静止开始运动，下降距离S时的加速度；2两段绳的张力；AODrR由于物块下降带动鼓轮沿水平直线路面纯滚动。鼓轮的质量为m,半径为R，r对质心轴C的回转半径为不计滚动阻力偶，绳子与轮之间不打滑。绳子位置的变化定滑轮处可以加主动力偶91\nBAOCA注意：该题的N多变化绳子跨过质量均为M，半径均为R，可以看成均质圆轮的定滑轮B，动滑轮C后，系在固定墙上。假设系统从静止开始运动。求：1物块A沿斜面向下运动S的加速度；2系在定滑轮B动滑轮C之间的那段绳的张力图示运动机构。物块A的质量为m，放在倾角为的光滑斜面上，系在质量不计的不可伸长的绳子上，1斜面与块间的动滑动摩擦系数动能的表达式发生变化吗？变化的是什么？92\nDABv注意：该题的N多变化2去掉斜面变化的是？DCABE3增加一个物块EBACO4去掉动滑轮加上一个辊子始末位置的动能全部力的功不变化的是解决问题的思路！！具体的量发生了改变！对固定轴的动量矩、力矩等！！假设二者的质量都为M,半径相等，均质盘，块C的质量为m,求辊子向下纯滚时中心的加速度动轮与定轮之间那段绳的张力粗糙斜面对辊子的摩擦力93\n注意：该题的N多变化BACO始末位置的动能全部力的功不变化的是解决问题的思路！！具体的量发生了改变！对固定轴的动量矩、力矩等！！假设二者的质量都为M,半径相等，均质盘，块C的质量为m,求辊子向下纯滚时中心的加速度动轮与定轮之间那段绳的张力粗糙斜面对辊子的摩擦力(沿斜面向上)94\n练习327综合题-21杆OA始终与斜面平行95\nBACOR图示运动机构。辊子A的质量为m，放在倾角为的粗糙斜面上，系在质量不计的不可伸长的绳子上，设绳子与所有的轮均不打滑绳子跨过质量均为m，半径均为R，可以看成均质圆轮的定滑轮B，动滑轮C后，系在固定墙上。假设系统从静止开始运动。求1辊子A沿斜面向下纯滚动距离S时轮心A的加速度；3系在定滑轮B动滑轮C之间的那段绳的张力（表示为所求的加速度的函数）2系在定滑轮B与辊子A之间的那段绳的张力（表示为所求的加速度的函数）作业？？96\nBACO不变化的是解决问题的思路！！假设二者的质量都为M,半径相等，均质盘，块C的质量为m,求辊子向下纯滚时中心的加速度动轮与定轮之间那段绳的张力粗糙斜面对辊子的摩擦力(沿斜面向上)作业97\n全部力的功想到的定理？？始末位置的动能铅直面内均质杆AB，长度为L，质量为m。A端搁在光滑的水平面上，B端用质量不计的绳悬挂在固定墙上某瞬时将绳剪断，求杆AB刚刚到达地面时的角速度杆AB的运动形式？杆AB动能计算公式？单独应用动能定理解决不了！！为什么？？动能定理的特点杆件的自由度？？BA98\nAB（二）对于两个自由度运动系统的问题二题目类型自由度ABABvAOAO99\n二题目类型（二）对于两个自由度运动系统的问题自由度z100\n（二）对于两个自由度系统的问题系统的动能必须表示成两个独立运动量的函数ABAO101\n绳子跨过质量均为m，半径均为R，可以看成均质圆轮的定滑轮B，动滑轮C后，系在固定墙上。物块E的质量为m假设系统从静止开始运动。求1物块A沿斜面向下运动S的加速度；2系在定滑轮B动滑轮C之间的那段绳的张力（表示为物块A的加速度的函数）图示运动机构。物块A的质量为2m，放在倾角为的光滑斜面上，系在质量不计的不可伸长的绳子上，RBAOCAER102\nBACOR图示运动机构。辊子A的质量为m，放在倾角为的粗糙斜面上，系在质量不计的不可伸长的绳子上，设绳子与所有的轮均不打滑绳子跨过质量均为m，半径均为R，可以看成均质圆轮的定滑轮B，动滑轮C后，系在固定墙上。假设系统从静止开始运动。求1辊子A沿斜面向下纯滚动距离S时轮心A的加速度；3系在定滑轮B动滑轮C之间的那段绳的张力（表示为所求的加速度的函数）2系在定滑轮B与辊子A之间的那段绳的张力（表示为所求的加速度的函数）作业？？103\nBACO不变化的是解决问题的思路！！假设二者的质量都为M,半径相等，均质盘，块C的质量为m,求辊子向下纯滚时中心的加速度动轮与定轮之间那段绳的张力粗糙斜面对辊子的摩擦力(沿斜面向上)作业104\n（二）对于两个自由度系统的问题系统的动能必须表示两个独立坐标的函数标量方程----只能求解一个未知量动能定理的特点？解决问题的方法？必须建立补充方程考虑除机械能守恒定律以外的守恒守恒动量守恒质心运动守恒对固定轴的动量矩守恒对质心轴的动量矩守恒受力分析运动初始条件BA105\n（二）对于两个自由度系统的问题例题1图示三棱拄A沿三棱拄B的表面滑动。A、B的质量分别为m1m2根据问题所求，首先想到的定理是？分析系统的自由度----两个如何建立补充方程？取系统为研究对象考虑守恒条件。若开始时系统静止，不计摩擦。求运动时三棱拄B的加速度运动的初始条件一定要进行受力分析不计摩擦开始时系统静止注意：计算动能用绝对速度！！系统在水平方向上动量守恒注意：计算动量也用绝对速度！！综合题5P323P254-255思考题10-5106\nx107\n综合题16P325解决问题的思路完全一致AC图示三棱拄ABC的质量为m1静止在光滑的水平面上，当质量为m2的均质圆柱由静止开始沿斜面AB向下纯滚动求三棱拄ABC的加速度考研的同学课下解决！！108\n思考根据问题所求，首先想到的定理是？例题2均质细直杆长L，质量m，静止直立于光滑水平面上分析杆的自由度----两个考虑守恒条件，建立补充方程？单个刚体可以考虑质心运动守恒杆受微小干扰而倒下时，求杆刚刚达到地面时的角速度。受力分析以及运动的初始条件受力分析告诉我们什么？系统初始静止质心C的水平方向的坐标？质心运动守恒！！P313例题12-12109\n启发特点2有没有固定的转轴？3初始条件？4摩擦的情况？解决问题的方法？动能定理+动量（质心运动）守恒有固定的轴动量一定不守恒！1两个自由度的系统ABAC如何区分？综合题16P325110\n思考根据问题所求，首先想到的定理是？例题3铅直平面内的均质的细杆OA可绕水平轴O转动，另一端铰接一均质圆盘，圆盘可以绕其中心A自由转动。分析系统的自由度----两个考虑守恒条件，建立补充方程AO设杆与盘的质量m，OA长度L，盘半径R。求自由释放后，杆与水平线成角的瞬时，初始时杆OA水平，系统静止。摩擦不计。杆的角速度和角加速度什么守恒？？综合题15P325111\n问自由释放后圆盘的运动形式？AOA受力分析！受力分析告诉我们什么？对质心的动量矩守恒运动的初始条件！没有绕质心的转动质心A点要运动！自由释放后圆盘的运动形式为平移若杆水平时系统静止。AO盘上任何点的速度都等于A点的速度112\n启发特点2有没有固定的转轴？3运动的初始条件4摩擦的情况解决问题的方法？？动能定理+对质心轴的动量矩守恒有固定的轴可以考虑对固定轴的动量矩守恒1系统两个自由度AO不能考虑动量守恒！！（质心）轴的动量矩守恒该题目对固定轴O的动量矩不守恒！113\nP323-324综合题—7解决问题的思路？自由度的分析z动能定理+对固定轴的动量矩守恒114\n动能定理也不是万能的板的质量为m1受水平力F的作用，沿水平面运动，板与水平面间的动摩擦因数为f在板上放置一质量为m2的均质圆柱，此圆柱对板只滚不滑求板的加速度自由度的分析有水平方向的主动力圆柱存在守恒的可能？无运动的初始条件单独解决P28611-26115\n第十三章达朗贝尔原理（动静法）116\n本章重点1惯性力的概念2刚体惯性力系的简化用动静法求解刚体动力学问题本章难点117\n§13-1惯性力、质点的达朗贝尔原理惯性力的概念1什么是质点的惯性力？2质点的惯性力特点？118\n§13-1惯性力、质点的达朗贝尔原理一、惯性力的概念由牛顿第二定律大小方向具有力的量纲－－定义为质点的惯性力119\n注意：惯性力的特点1凡是具有质量的质点，只要运动状态发生改变，必然有惯性力质点具有惯性力的两个必要条件----缺一不可2惯性力矢量可以投影，可以计算力矩惯性力作为力的共性3惯性力作用在何处？惯性力作用在使质点获得加速度的其它物体上惯性力的个性4瞬时值---要用绝对加速度计算惯性力牛顿第二定律的产物120\n判断题1凡是运动的质点都有惯性力2惯性力是作用在质点上的3质点在空中运动，只受到重力作用，质点的惯性力只与那两个必要条件有关当质点作自由落体运动，质点被上抛，质点被平抛时，质点的惯性力是不相同。121\n真正作用在质点在主动力，约束反力以及虚加在质点上的惯性力二质点的达朗贝尔原理真正作用在质点上的力作用在何处？§13-1惯性力、质点的达朗贝尔原理在形式上构成平衡力系注意：1形式上的平衡2解决问题时用投影式动静法122\n三思考题1应用动静法时，对静止的质点是否需要加惯性力？2对运动的质点是否都要加惯性力？3应用动静法可以解决什么样的问题？§13-1惯性力、质点的达朗贝尔原理123\nBAO例题1圆盘可绕轴O转动，质量不计。其上缠有一质量不计的绳，绳不可伸长，绳下端分别吊重物AB。若圆盘半径为Rr，重物AB的质量MA大于MB并设绳与圆盘间无相对滑动。若盘的角加速度为已知要求：1计算A、B惯性力的大小2标上惯性力的方向注意：虚加的位置实线？？虚线124\n§13-2质点系的达朗贝尔原理质点系的的达朗贝尔原理（i=1-----n）对于质点系中的质点，所受主动力、约束力实际上就是外力、内力。（i=1-----n）125\n真正作用在质点系上的外力真正作用！虚加！！虚加！和虚加在每个质点上的惯性力，质点系的的达朗贝尔原理§13-2质点系的达朗贝尔原理在形式上构成平衡力系应用时视力系的情况进行求解！！126\nBAO例题2圆盘可绕轴O转动，质量不计。其上缠有一质量不计的绳，绳下端分别吊重物AB。若圆盘半径为Rr，重物AB的质量MA大于MB并设绳与圆盘间无相对滑动。要求用动静法计算1盘的角加速度2O处的约束力1取系统为研究对象，受力分析2对质点系的所有质点虚加惯性力MBgMAgFOxFOy与各自的加速度的方向相反3列”平衡”方程注意：按照虚加的方向进行投影和计算力矩127\n关于17周周六课的补课问题时间：17周周四一二节地点：五号教学楼102教室时间：17周周四一二节地点：五号教学楼102教室本周六1-2节本教室答疑128\n§13-3刚体惯性力系的简化1为什么要进行简化？2如何进行简化？3刚体惯性力系简化的结果预备知识力系的主矢的定义以及与简化中心有无关系？力系的主矩的定义以及与简化中心有无关系？平移刚体的判断以及运动特点（加速度）定轴转动刚体的判断，以及质心加速度的计算平面运动刚体的判断，以及质心加速度的计算刚体转动惯量的计算质心运动方程129\n要求用动静法求质量m,半径为r的均质圆轮,从倾角为的粗糙向下纯滚。1轮子的角加速度2轮子受到的摩擦力07年考试题目考研的同学课下做一下130\n曲柄连杆滑块机构中。OA=AB=L。OA的角速度大小不变。求：1、AB杆的角速度；B的速度2、AB杆的角加速度；杆AB的角加速度等于零wB45ºOA90º方向图示转向顺时针AB杆中点C的加速度131\n45º90º90ºO1OBAw杆AB的角加速度等于零已知四连杆机构中O1B＝L，AB＝2LOA以不变绕O轴转动。求：1图示位置时O1B杆的角速度杆AB的角速度2B点的加速度杆AB的角加速度逆时针逆时针如何求AB杆中点的加速度？132\n60º90ºO1OBAwOA=LO1B=4L图示位置AB铅直O、A、O1水平OA匀角速度1求杆AB、O1B的角速度2求杆AB的角加速度顺时针顺时针AB杆中点C的加速度133\nDCBqFAMbaaP1.5a一求杆BC所受的力二固定端A处的约束力a134\nRR两个均质圆盘完全相同，质量M半径R第一个盘在受主动力作用加速转动第二个盘在一重物作用下加速转动问两盘的角加速度是否相同？？定轴转动微分方程与质点系对固定轴的动量矩定理的区别135\n下周三3-4节5号教学楼408教室答疑用动能定理时不必画受力图下周三3-4节5号教学楼408教室答疑下周三1-2节5号教学楼108教室上课136\n作业中存在的问题1动能定理错误2固定轴的动量矩定理与定轴转动微分方程？？3不画受力图4受力图不正确ACBDAAmg2mgFcxFcyFT137\n§13-3刚体惯性力系的简化1为什么要进行简化？2如何进行简化？3刚体惯性力系简化的结果预备知识力系的主矢的定义以及与简化中心有无关系？力系的主矩的定义以及与简化中心有无关系？平移刚体的判断以及运动特点（加速度）定轴转动刚体的判断，以及质心加速度的计算平面运动刚体的判断，以及质心加速度的计算刚体转动惯量的计算质心运动方程138\n§13-3刚体惯性力系的简化1为什么要进行简化？2如何进行简化？惯性力系的主矢惯性力系对简化中心O的主矩惯性力系为平面时为代数量将复杂问题简单化仿照静力学进行P40与简化中心的位置有无关系？与简化中心的位置有无关系？BAO计入圆盘的质量139\n3刚体惯性力系简化的主要结果刚体的平行移动刚体绕固定轴的转动刚体的平面运动§13-3刚体惯性力系的简化（重点掌握）本章的第二个重点内容140\n§13-3刚体惯性力系的简化一、平移刚体2以质心C为简化中心1惯性力系的主矢注意：只对质心点的主矩等于零3结论思考：以那点为简化中心，简化结果最简单？平移刚体的运动特点？平移刚体惯性力系可以简化为通过质心的合力大小等于刚体的质量与加速度的乘积方向与加速度的方向相反P334141\nO1O2ABCR铅直平面内的平行四连杆机构，O1A=O2B=L，O1A位于铅直位置。杆AB的质量为m质心C距A的距离为R杆AB的运动形式？简化结果要求：杆AB惯性力系的简化结果回忆平移刚体惯性力系的简化结果方向以及位置！！！实线虚线思考将上述结果搬到A（B）不做任何改变是否可以？以简化在质心上的结果为原始情况，可以向任意点简化142\n二定轴转动刚体（一）对刚体的要求：刚体有一个质量对称平面转动轴与质量对称平面垂直（二）对简化中心的要求轴心（转动轴与质量对称平面的交点）O§13-3刚体惯性力系的简化（三）简化结果1惯性力系的主矢思考虚加在那里？2惯性力系的主矩表示？如何计算？3结论具有质量对称平面且转轴垂直于质量对称平面的定轴转动刚体P336143\n注意：2记住简化结果3要计算惯性力系主矢的大小主矩的大小4虚加的位置5方向转向以及虚线（实线）例题计算并在图上标出下列给定的具有质量对称平面的质量为m的均质刚体在图示位置图示瞬时惯性力系的简化结果。1要判断刚体的运动形式回忆1平移刚体惯性力系的简化结果回忆2具有质量对称面且转轴与质量对称面垂直的转动刚体惯性力系的简化结果144\nOOL/3A半径为R半径RAOL共性回忆具有质量对称面且转轴与质量对称面垂直的转动刚体惯性力系的简化结果145\n简化结果半径为R146\n共性简化结果半径为RO（四）特例1转轴过质心角加速度不等于零2转轴过质心，角加速度等于零147\nO共性简化结果148\n三、平面运动刚体1运动分解（一）对刚体的要求刚体有一个质量对称平面（二）处理问题的方法随质心C的平移绕质心C的转动第11章讲授科学的工作方法？§13-3刚体惯性力系的简化2惯性力分解随质心C的平移部分的惯性力按平移刚体惯性力的简化方法进行绕质心C的转动部分的惯性力定轴转动刚体的特例转轴过质心角加速度不等于零！分而制之！149\n三、平面运动刚体（三）结论P3361主矢大小方向虚加在2主矩大小转向虚加在MIC§13-3刚体惯性力系的简化质量为m半径为RCa向左纯滚动的均质园轮a向下运动的均质圆盘共性回忆平面运动刚体惯性力系的简化结果150\n简化结果Ca向左纯滚动的均质园轮151\n§13-3刚体惯性力系的简化质量为m半径为Ra向下运动的均质圆盘回忆平面运动刚体惯性力系的简化结果简化结果向下运动152\n总结1刚体惯性力系简化首先要分析刚体的运动形式2刚体惯性力系的简化结果平移刚体P334定轴转动刚体P336平面运动刚体P336与计算刚体的动量矩动能类似153\nOA例题1铅直平面内的均质杆OA质量m杆长L。A端系一质量不计的细绳，静止在水平位置。某瞬时将绳剪断。要求用动静法求该瞬时杆的角加速度；O处的约束力1取研究对象（系统）受力图O2运动分析虚加惯性力3建立“平衡”方程按照虚加惯性力的方向（转向）进行154\n例2汽车的一个主动轮可以简化为半径为R、质量为m的圆轮。假定圆轮对轮心(质心)的回转半径为,在其上作用力偶矩为M的主动力偶,圆轮沿水平粗糙直线路面向右作纯滚动。不计滚动阻力偶。要求用动静法求，图示瞬时:(1)圆轮的角加速度;(2)轮心的加速度；(3)地面对圆轮的摩擦力；M155\n1研究对象受力分析3求解2运动分析虚加惯性力M思考摩擦力的指向？？半径为R、质量为m向右纯滚动对轮心(质心)的回转半径M思考角加速度的转向？思考补充方程如何建立？注意：题目中不要求用该法时千万不要用！！156\n本章总结1惯性力的概念---2刚体惯性力系的简化质点具有惯性力的两个必要条件------缺一不可惯性力作用在使质点获得加速度的其它物体上要用绝对加速度计算惯性力以课堂例题为母题3存在惯性力的平衡是形式上的平衡4动静法单独应用时除非特别说明否则千万不要用157\n理论力学大总结三大篇研究对象刚体（系统）静力学第二章平面任意力系简化物体系统平衡运动学第七章第八章点的速度合成定理点的加速度合成定理有关速度和角速度的计算有关加速度和角加速度的计算单独出题动力学动量定理以及守恒动量矩系列定理以及守恒动能定理重点是综合应用静定结构或平衡的机构158\n一动力学基本量计算（思考题10-1思考题11-3母题惯性力）均质杆质量M，L。均质盘（轮、柱）R，m。焊接为一体。AO注意：两者之间的根本区别焊接一系列公式铰接AO动量动量矩动能惯性力系简化159\n平行四连杆机构。均质杆AB质量M，LO1O2ABCva均质圆盘，质量MR直线路面纯滚动160\n二普遍定理单独应用不再总结三普遍定理综合应用动能定理课堂例题以及作业重点一个自由度的系统动量矩定理的系列定理动量定理（质心运动定理）机构两个自由度的系统动能定理除机械能守恒以外的守恒定理课堂上的例题机构母题综合-13母题1P313-314求角速度2综合题15注意：动量矩定理的系列定理的适用条件161\n静力学有关的概念----第一章全部概念包括课上思考题第二章全部概念包括课上思考题第二章简化问题桁架的零杆问题课上思考题第三章力在坐标轴上的投影力对坐标轴的矩重心第四章摩擦力的计算摩擦角以及自锁条件课上思考题课上思考题162\n曲柄连杆滑块机构中。OA=AB=L。OA的角速度大小不变。求：1、AB杆的角速度；B的速度2、AB杆的角加速度；杆AB的角加速度等于零wB45ºOA90º方向图示转向顺时针AB杆中点C的加速度163\n45º90º90ºO1OBAw杆AB的角加速度等于零已知四连杆机构中O1B＝L，AB＝2LOA以不变绕O轴转动。求：1图示位置时O1B杆的角速度杆AB的角速度2B点的加速度杆AB的角加速度逆时针逆时针如何求AB杆中点C的加速度？164\n60º90ºO1OBAwOA=LO1B=4L图示位置AB铅直O、A、O1水平OA匀角速度1求杆AB、O1B的角速度2求杆AB的角加速度顺时针顺时针AB杆中点C的加速度165\n平面任意力系简化问题以作业P662-10为母题简化中心主矢主矩的计算是否需要进一步简化？？力偶如何处理！166\n下周三3-4节5号教学楼408教室答疑用动能定理时不必画受力图圣诞快乐下周三3-4节5号教学楼408教室答疑167\n新年快乐168\n2-41P75母题----外部约束力1轮子的处理（不单独取研究对象）2二力杆的处理（不单独取研究对象）3销钉的问题4固定端支座的约束力的问题约束力偶不准漏掉5列方程时集中力集中力偶分布载荷6一个研究对象一个受力图是否带上销钉的问题7课堂上讲得其它的注意问题作用力为负值反作用力也是负值静力学平衡状态P742-40169\nDCBqFAMbaaP1.5a一求杆BC所受的力二固定端A处的约束力a170\n2-39404142P74-75母题----外部约束力P722-29为母题ABC3R2R2RGDE母题P722-31内力+外力注意：2-31中E处的约束力课堂上的例题以及全部作业题171\n要求用动静法求质量m,半径为r的均质圆轮,从倾角为的粗糙向下纯滚。1轮子的角加速度2轮子受到的摩擦力不计入滚阻力偶FS172\n本周六1-2节5号教学楼105教室答疑本周六1-2节5号教学楼105教室答疑用动能定理时不必画受力图圣诞快乐173\n习题2-392-402-41DE折杆的受力特点？定滑轮如何处理？希望取那个研究对象求A处的约束力？？T字形杆+斜杆CD带上滑轮D处的销钉是否带上？？FAyFDEDPFqFAxMA中间未知量如何解决？FDEFDPFCxFCyFAyFDEDPFqFAxMA174\nABC3R2R2RGDE图示结构由不计杆重的两杆ADBC和半径R的滑轮组成.求AB处的约束力。2-29为母题175\n单面约束双面约束双面约束的约束力可以从满足要求的任何方向指向受力体DBA176\n运动学第五章第六章概念课堂上的概念点的运动直线运动曲线运动平面曲线空间曲线圆周运动一般平面曲线空间曲线考试不涉及不涉及到力的运动机构177\n刚体的运动简单运动复杂运动平移转动直线平移曲线平移平面运动各点轨迹各点轨迹各点轨迹直线圆周一般平面曲线各点轨迹178\nqOACDO1wO2ABM平行四连杆机构45º90º90ºO1OBAw四连杆机构AOB曲柄连杆机构179\n第七章三个定理2牵连运动为平移时点的加速度合成定理3牵连运动为转动时时点的加速度合成定理1速度合成定理对牵连运动的形式无任何限制一要求用点的合成运动的方法求解180\n二动点动系选取的几种情况qOACDCAqBObOCD母题7-77-87-97-17滑块连接7-57-197-21不变的接触点7-20变化的接触点以速度计算为主181\n三三个非常重要的概念1牵连速度(加速度)AOBMAOBM‘182\n图示瞬时OA与水平线的夹角60度。求轮心C的速度加速度OA杆转动，带动半径为R的园轮转动。C牵连速度牵连加速度如何确定？OAO1183\n已知动点的相对运动方程时未知动点的相对运动方程时求相对速度必须由速度合成定理求出求相对加速度相对运动轨迹为直线时相对运动轨迹为轨迹已知的曲线时三三个非常重要的概念相对加速度的切线方向量通过加速度合成定理分析求得经过加速度合成定理分析求得2相对速度(加速度)参考作业7-21184\n三三个非常重要的概念3科氏加速度AOBM条件：牵连运动为转动(复杂的运动)牵连运动刚体的角速度矢与动点的相对速度矢不平行qOACD185\n三三个非常重要的概念3科氏加速度OCDCAqBObAMO1O2w186\n5)画出加速度矢量图。并计算各量的大小、画出方向(未知指向可以假设)(必须有)6)求解(必须有)注意：如何选投影轴?如何写投影方程?1)动点动系的选取(必须有)3)速度分析定理必须有2)分析三种运动特别关注牵连运动的形式画好速度矢量图（必须有）4)加速度定理的表达形式(必须有)若牵连运动为转动还要计算牵连转动的角速度和相对速度根据牵连运动的形式决定加速度定理的内容课上例题以及全部作业题题目必备187\n几个概念4瞬时速度中心位置的确定第八章瞬时速度中心点的加速度一定不等于零1瞬时平移与平移的区别2瞬时转动与定轴转动的区别3是平面图形的绝对角速度和绝对角加速度不涉及复合（合成）运动，且一定有平面运动刚体的运动机构平面运动的图形188\n一求速度（角速度）的方法1基点法2瞬时速度中心法都可以求平面图形的角速度3速度投影法不能求平面图形的角速度原始的方法，要求其它点的速度还要继续使用基点法------慢可以快速求平面图形上N多点的速度------简单快需要知道待求点的速度方位------简单瞬心确定的两种方法可以联合应用瞬心法与速度投影法189\n二求加速度（角加速度）的方法方法单一基点法关于公式的正确性关于基点的选择----基点的加速度必须已知190\n1运动分析---明确平面运动的刚体1）选基点(加速度已知)3加速度分析2速度分析2）针对加速度公式分析已知与待求画出加速度矢量图3）求解计算各个已知量的大小，并将方向标在矢量图上根据题目要求选择简单快的方法进行必须求出平面图形的角速度根据待求点的轨迹情况写出公式课堂例题以及全部作业题题目必备在待求加速度点画加速度矢量图191\n若待求点B的轨迹为圆周运动则公式为若待求点B的轨迹为一般的平面曲线则公式为若待求点B的轨迹为直线则公式为待求加速度点相对于基点的加速度之间的关系特别注意192\n成长感动感谢祝福爱人者人恒爱之敬人者人恒敬之己所不欲勿施于人193