大学物理-衍射 49页

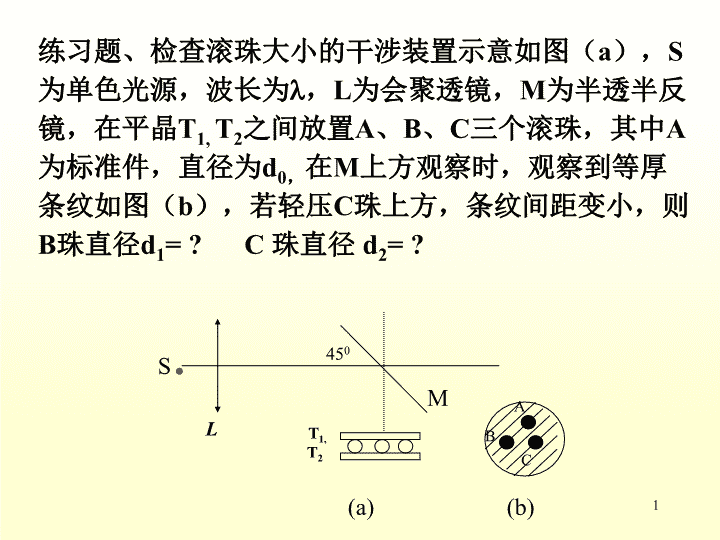
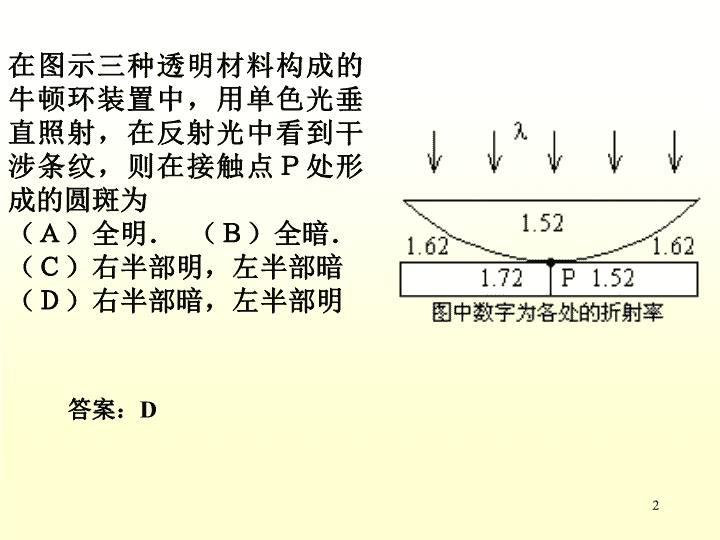
练习题、检查滚珠大小的干涉装置示意如图（a），S为单色光源，波长为，L为会聚透镜，M为半透半反镜，在平晶T1,T2之间放置A、B、C三个滚珠，其中A为标准件，直径为d0，在M上方观察时，观察到等厚条纹如图（b），若轻压C珠上方，条纹间距变小，则B珠直径d1=?C珠直径d2=?S.450MT1,T2ABC(a)(b)L1\n在图示三种透明材料构成的牛顿环装置中，用单色光垂直照射，在反射光中看到干涉条纹，则在接触点Ｐ处形成的圆斑为（Ａ）全明．（Ｂ）全暗．（Ｃ）右半部明，左半部暗（Ｄ）右半部暗，左半部明答案：D2\n6.4光的衍射6.5夫琅和费的单缝衍射6.6夫琅和费圆孔衍射6.7光栅衍射3\n6.4光的衍射(diffractionoflight)一、光的衍射现象(2)f单狭缝透镜P观察屏of圆孔透镜P观察屏o*s观察屏o小圆孔小圆板观察屏o4\n二、惠更斯——菲涅耳原理波传到的任何一点都是子波的波源，各子波在空间某点的相干叠加，就决定了该点波的强度。远场衍射(2)夫琅禾费衍射近场衍射(1)菲涅耳衍射分类:··pdE(p)rQdSS(波前)设初相为零n光在传播过程中能绕过障碍物的边缘而偏离直线传播的现象。定义:5\n6.5夫琅和费的单缝衍射一.装置(缝宽)S:单色光源:衍射角·*Spffa透镜L透镜LAB缝平面观察屏0δ二.半波带法aABaqGG1G2asinqCc1c2c3半波带6\n分成偶数个半波带aθ2BA半波带半波带1l/2半波带半波带121’2’c—暗纹k=1,2,3分成奇数个半波带k=1,2,3—明纹q↑→波带数↑→光强↓不能分成整数个半波带1’2’光强介于最强与最暗之间——中央明纹(中心)OHL7\n三、明暗纹条件——暗纹(中心)——明纹中心(近似)——中央明纹(中心)若asinq不是半波长的整数倍，亮度介于最明和最暗之间。8\n四、光强分布/a-(/a)2(/a)-2(/a)sin0.0470.0171I/I00相对光强曲线0.0470.017五.条纹宽度ΔxIx1x2衍射屏0观测屏Δx0半I1=4.7%I0I2=1.7%I0I3=0.8%I01.角宽度某一亮纹的角宽度为该亮纹两侧两相邻暗纹中心对透镜光心所张的角度。l透镜f9\n中央明纹角宽度其它次极大——衍射反比定律ΔxIx1x20Δx0半fk级明纹角宽度2亮纹的线宽度中央亮纹10\n讨论：1波长对条纹宽度的影响缝宽a一定，l↑Dq↑Dx∝l，波长越长，条纹宽度越宽2缝宽变化对条纹的影响缝宽越小，条纹宽度越宽当时，屏幕是一片亮当a>>l时，I0sin∴几何光学是波动光学在/a0时的极限情形只显出单一的明条纹单缝的几何光学像(1)(2)11\n3、白光入射单缝中央白色明纹两侧对称彩带，由紫到红4、单缝上下平移，屏上衍射条纹位置不变1级光谱2级光谱-1级光谱-2级光谱中央明纹ΔxIx1x2衍射屏0观测屏Δx0半l透镜f5、以上明、暗纹公式只适用于平行光垂直单缝入射，入射光线倾斜，需考虑入射光的光程差。12\n例：如图所示单缝衍射装置，缝宽a=0.5mm，f=50cm，用可见光照射单缝，在观察屏上x=1.5mm处看到明纹极大，求：（1）入射光的波长及衍射级次（2）单缝所在处的波阵面被分成的波带数目。jf解：明纹=0.003<5°sin=0.003(Å)(Å)k=1l1=10000(Å)红外k=2l2=6000(Å)k=3l4=3333(Å)可见光k=4紫外l3=4286(Å)13\n2波带数目k=2l2=6000(Å)k=3l3=4286(Å)N=2k+1=5N=2k+1=7/a-(/a)2(/a)-2(/a)sin0.0470.0171I/I00相对光强曲线0.0470.01714\n例单缝夫琅禾费衍射,己知:a=0.3mm,f=12.62cm第五级喑纹之间距离L=0.24cm;求:1),2)k=5的暗纹对应的半波带数。解:1)a·sin5=kk=5(1)L=2x5(2)x5=f·tan5(3)由(1)得:代入(3):2)2k=10个半波带(14)=5705[Å]15\n例.用1=400nm和2=700nm的混合光垂直照射单缝;1的第k1级明纹恰与2的第k2级暗纹重合;求:(1)k1,k2;解:(1)1的明纹条件与2的暗纹条件:16\n例平行单色光以角入射单缝，求中央明纹位置。折射率nOO12f空气解：平行光斜入射，中央明纹不在O点处。中央明纹对应衍射光线等光程点，设其为O点，则光程差当n=1时，=17\n例单缝衍射实验中，(1)单缝上下移动小距离，屏上衍射图样是否改变？(2)光源上下移动小距离，屏上衍射图样是否改变？SfSf(1)平行于主光轴(或同一条副光轴)的所有光线会聚于同一点,所以衍射图样不改变。S(2)下移光源，相当于平行光斜入射单缝，衍射图样将上移。(参考例题)18\n§6.6夫琅和费圆孔衍射SDf圆孔衍射条纹的特点：1.中央是一个圆亮斑，称为爱里斑，约98%的光强集中于此。随后的亮环越来越暗，间隔不等。2.1级暗环的衍射角由Dsin1=1.22决定，所以爱里斑的半径为I19\n一、光栅1.定义—大量等宽等间距的平行狭缝(或反射面)构成的光学元件。d反射光栅d透射光栅a是透光（或反光）部分的宽度d=a+b光栅常数b是不透光(或不反光)部分的宽度3.光栅常数2.种类：晶体-天然光栅一般光栅几十—几千条缝/mm6.7光栅衍射(gratingdiffraction)20\n光栅常数d与缝数/cm（刻痕/cm)成倒数关系abd例：8000/cm=1.25×10-4(cm)光栅缝数NN,d光栅的重要常数21\n二、光栅衍射1装置与光路qqPOP0L多光束干涉+单缝衍射2多光束干涉dbaqACq123456dsinqdsinqdsinq=±klk=0,1,2…d=a+bP为明纹（主极大）N个A=NA0I=N2I0—光栅方程B22\n0/d-(/d)-2(/d)2/dII0sinN=4光强曲线/4d-(/4d)-2-1012k极小如N=4,有三个极小1234/24112343/223\n极小值位置初相差合振幅为零qCq123456dsinqdsinq——极小值位置24\n条纹特点：几乎黑的背景上的又细、又亮条纹I=N2I0缝数N很大123456取j’=1ABCD25\n相邻主极大之间分布着（N-1)个极小，(N-2)次极大0/d-(/d)-2(/d)2/dII0sinN=4光强曲线/4d-(/4d)26\n3单缝衍射I单sin0I0单-2-112/ak’-/asinI/d-(/d)-7-6-5-4-3-2-101234567k-8IN2I0单sin048-4(/d)单缝衍射轮廓线光栅衍射光强曲线N=4d=4a4光栅27\n5缺级定义：当多缝光束干涉的主极大恰好与单缝衍射的极小位置重合时，该极主极大将在屏幕上消失的现象。k’=1,2…k=0，1,2…单缝衍射极小多光束干涉主极大k’=1,2…——缺级条件例：d=16000Åa=8000Åd/a=2k’=1,2…缺±2，±4，±6，…28\n例：求单缝衍射中央明纹内的条纹数。d/a=整数解：k’=1条纹数目：（条）6衍射图样特点qqPOP0L(1)P0处为明纹，两侧出现明暗相间的花纹。(2)明纹亮、细锐，亮度随N的增大而增大(3)I=N2I0N↑→明纹越细且条纹明暗对比越强。29\n例：用5000/cm的平面透射光栅观察钠黄光谱线，l=5893Å求：(1)光线垂直入射时，第三级谱线的衍射角有多大？(2)光线以30°角入射时，最多可看到几级条纹？解：(1)(cm)=2×104Åk=3=±0.884q3=±62°12′(2)斜入射k=0，1,2…——光栅方程+q、j在法线的同侧-q、j在法线的两侧jABCDq12q1’2’E=±5以+为例30\nd=4a-8Isin048-4(/d)例：波长为l=600nm的单色光垂直入射在一光栅上，第2，3级明条纹分别出现在sin=0.20与sin=0.30处，第四级缺级。试求：(1)光栅常量(2)光栅上狭缝宽度(3)屏上实际呈现的全部级数解：dsinq=±klk=0,1,2…(1)光栅方程0.2d=2ld=10l=6000nm(2)d=4a(3)理论实际观察到的是9级能够出现k=0，1，2，3，④，5，6，7，⑧，931\n例:激光器发出红光:=6328Å垂直照射在光栅上,第一级明纹在38º方向上,求:1)d?2)第三级的第1条缝与第7条缝的光程差?3)某单色光垂直照射此光栅,第一级明纹在27º方向上,此光波长为多少?解:1)2)第三级相邻两缝之间衍射光的光程差为3则第1条缝与第7条缝的光程差为(7-1)3=101248[Å]3)(37)d·sin=kd·sin38º=6328[Å]=10278[Å]'=10278sin27º=4666[Å]32\n例波长为l1=5000Å和l2=5200Å的两种单色光垂直照射光栅,光栅常数为0.002cm,f=2m,屏在透镜焦平面上。求(1)两光第三级谱线的距离;(2)若用波长为4000Å7000Å的光照射,第几级谱线将出现重叠;(3)能出现几级完整光谱？解:(1)(40)33\n当k=2,从k=2开始重叠。(2)设1=4000Å的第k+1级与2=7000Å的第k级开始重叠(41)1的第k+1级角位置:2的第k级角位置:12-1-20-33(3)能出现28级完整光谱34\n例：一衍射光栅对某一定波长的垂直入射光,在屏幕上只能出现零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该(A)换一个光栅常数较小的光栅。(B)换一个光栅常数较大的光栅。(C)将光栅向靠近屏幕的方向移动。(D)将光栅向远离屏幕的方向移动。选[B]dsinq=±kl35\n例：对应于衍射角=30o,单缝处的波面可划分为4个半波带,则单缝的宽度a=_________(为入射光波长)。4aABaqGG1G2asinqCc1c2c3半波带36\n单缝衍射a=10双缝衍射a=10,d=40杨氏双缝干涉和双缝衍射的区别:(25)单缝衍射中央零级明纹范围:当a→时,→/2双缝衍射演变成杨氏双缝干涉a=2,d=4037\n例：波长=6000Å的单色光垂直入射到一光栅上，测得第二级主级大的衍射角为30o且第三级是缺级，1)光栅常数等于多少；2)透光缝宽度a等于多少；3)选定了上述d和a后，求在屏幕上可能呈现的主级大的级次。解：1）由光栅衍射，主极大公式得：2）缺级公式38\n3)由因为第3级缺级，所以实际呈现得等各级主级大。39\n例：利用一个每厘米刻有4000条缝的光栅，在白光垂直照射下，可以产生多少清晰可见完整的光谱？问哪一级光谱中的哪个波长的光开始与它谱线重叠？由解:设对第k级光谱，角位置从到，要产生完整的光谱，即要求的第(k+1)级纹在的第k级条纹之后，亦即根据光栅方程40\n或得设第二级光谱中波长为的光与第三级中紫光开始重叠，这样所以只有才满足上式，所以只能产生一个完正的可见光谱，而第二级和第三级光谱即有重叠出现。41\n解：<1>[例]l=6000Å入射光栅，第二级明纹出现在sinq=0.2处，第四级缺级。<1>a+b=？<2>缝宽；<3>屏上实际出现的条纹数；<4>若入射光以30o角斜射，能够观察到的明纹最高级次。条纹数？<2>k=4为第1次缺级<3>能够出现k=0，1，2，3，④，5，6，7，⑧，91+27共=15(条)<4>OPfa+blf30o理论实际观察到的是14级42\n两块平玻璃构成空气劈尖，左边为棱边，用单色平行光垂直入射．若上面的平玻璃慢慢地向上平移，则干涉条纹（Ａ）向棱边方向平移，条纹间隔变小．（Ｂ）向棱边方向平移，条纹间隔变大．（Ｃ）向棱边方向平移，条纹间隔不变．（Ｄ）向远离棱边的方向平移，条纹间隔不变．（Ｅ）向远离棱边的方向平移，条纹间隔变小．答案：C43\n若把牛顿环装置（都是用折射率为1.52的玻璃制成的）由空气搬入折射率为1.33的水中，则干涉条纹（Ａ）中心暗斑变成亮斑．（Ｂ）变疏．（Ｃ）变密．（Ｄ）间距不变．答案：CDe=e’-e44\n证：(1)[例]在杨氏双缝干涉中，光源S偏离中心轴OO，而与缝S2位于同一水平面，参数如图，D>>a，(空气中)。证：(1)屏幕上零级明条纹的位置处，(2)原中央零级明纹(即O点)，现为第10级明纹。(设)SS1S2PDr1r2qqOxx0O4a(2)O点处对应的光程差：O点处的明条纹视为第10级明纹下移上移2a45\n例:黄光=600nm垂直照射在平行平面肥皂膜上(n2=1.33)如反射光恰好是第一级明纹,求肥皂膜的厚度e?黄光在肥皂膜内的波长。解:1)n1=1,n2=1.33,k=12)n1n246\n解:设l为玻璃容器的长度,用被测气体代替空气后光程差的改变量为2(n－n0)l例:用钠光灯(=589.3nm)作光源,在迈氏干涉仪的一支光路上,放置一长度为140mm的玻璃容器,当以某种气体充入容器时,观察干涉条纹移动了180条求:该种气体的折射率n=?(空气的n0=1.000276)12M1M2M2G1G2SE半透半反膜47\n光的衍射现象夫琅和费衍射单缝夫琅和费衍射(半波带法分析)中央明纹:=0k级暗纹中心:asin=2k/2k级明纹中心:asin=(2k+1)/2光栅衍射光栅方程(垂直):(a+b)sin=k缺级:惠更斯-菲涅耳原理48\n作业6-14、6-15、6-17、6-20、6-21、6-24第六章波动光学(WaveOptics)49