大学物理热学 39页

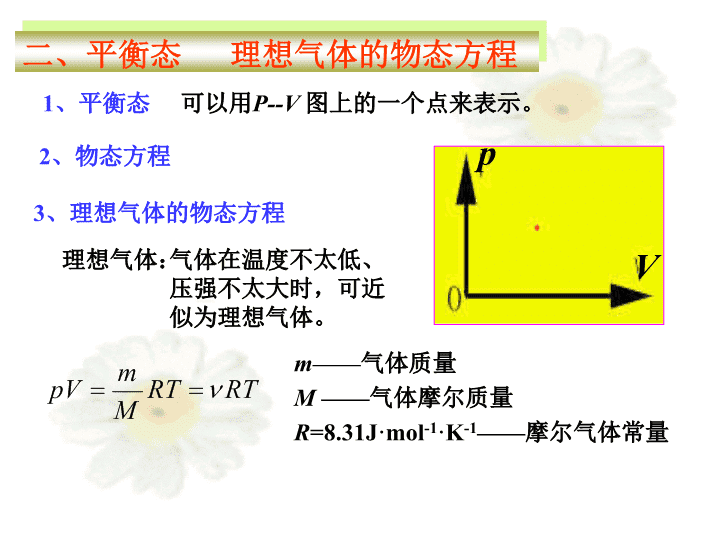
热学1．什么是热学2．两种研究方法以物质的热运动以及热运动与其它运动形态之间的转化规律为研究对象的一门学科。热力学——宏观理论不涉及物质的微观结构。第十三章统计物理学——.第十二章\n12－1气体物态参量平衡态理想气体物态方程一、气体物态参量第十三章热力学基础p、V、T1.气体压强P：力学描述.2.体积V：几何描述.3.温度T：热学描述单位：温标K（开尔文）.\n二、平衡态理想气体的物态方程1、平衡态可以用P--V图上的一个点来表示。pV2、物态方程3、理想气体的物态方程理想气体：气体在温度不太低、压强不太大时，可近似为理想气体。m——气体质量M——气体摩尔质量R=8.31J·mol-1·K-1——摩尔气体常量\n可用Ｐ－V图上的一条有方向的曲线表示。13-1准静态过程功热量一、准静态过程元功：系统体积由V1变为V2，系统对外界作总功为：二、功准静态过程系统对外界做功：\n注意：2、功等于P—V图上过程曲线下的面积,体积增加取正,减小取负。3、功是过程量功与过程的路径有关，V不变时W=01、V，W>0；V，W<0或外界对系统作功4、作功是改变系统内能的一种方法。Q单位：J(焦耳)①热量与功一样都是过程量。说明：②传递热量和作功都可改变系统的内能三、热量\n所有分子各种热运动（包括平动，转动和振动）能量和分子间相互作用势能13－2热力学第一定律内能一、内能说明：①改变内能的方式：做功，传递热量。②内能E是状态量，因此内能变化△E仅与始末状态有关，与过程无关.2AB1**2AB1**\n实际气体③理想气体的内能仅是温度的函数单原子分子刚性双原子分子刚性多原子分子温度越高内能越大i：自由度\n二、热力学第一定律对于微小过程符号规定+系统实际吸热系统实际放热内能增加内能减少系统对外做正功即：体积增加系统对外作负功或外界对系统做功即:体积减小（1）对于理想气体准静态过程有：(2)热力学第一定律是包括热现象在内的能量守恒定律对任何物质的任何过程都成立.注意Q：系统吸热W：系统对外做功\n13-14.如图所示，系统从状态A沿ABC变化到状态C的过程中，外界有326J的热量传递给系统，同时系统对外作功126J。当系统从状态C沿另一曲线返回到状态A时，外界对系统作功为52J，则此过程中系统是吸热还是放热？传递热量是多少？解：ABC过程J126ABC=WJ,326ABC=QJ200ABCABCAC=-=DWQE从C到A过程：负号表示系统向外界放热252J。J200CA-=DEJ252CACACA-=+D=WEQ\n1.等体过程V=恒量T2T1pV0ab第一定律特点：13－3理想气体的等体过程和等压过程摩尔热容一、等体过程定体摩尔热容WV=0过程方程：功、热量、内能的变化过程曲线：吸收的热量全部用来内能增加;或向外界放热以内能减小为代价;系统对外不作功。\n3、理想气体定体摩尔热容定义：1mol、等体过程升高1度所需的热量等体过程吸热等体过程内能的增量理想气体的内能另表述：理想气体准静态过程热力学第一定律：\nP=恒量第一定律特点：吸收的热量一部分用来内能增加，一部分用来对外做功。二、等压过程定压摩尔热容1、等压过程过程方程：功、热量、内能的变化过程曲线：\n2、定压摩尔热容定义：1mol、等压过程中升高1度所需的热量。等压过程的吸热Mayer公式等压过程第一定律\n摩尔热容比泊松比1.67单原子分子理想气体双原子分子理想气体多原子分子理想气体1.401.33\n等容等压欲求W，Q或ΔE，要会用状态方程求出P、V、T、ν\n13-13：一压强为1.0×105Pa，体积为1.0×10-3m3的氧气自0℃加热到100℃,问:(1)当压强不变时,需要多少热量?当体积不变时,需要多少热量?(2)在等压或等体过程中各作了多少功？解：根据题意得（1）（2）得:由或用热力学第一定律求解。\nT=恒量pVp1p2III..OV2V113－4理想气体的等温过程和绝热过程一、等温过程过程方程：功、热量、内能的变化第一定律特点：吸收的热量全部用来对外作功，内能保持不变。过程曲线\n二、绝热过程1、绝热过程Qa=0功、热量、内能的变化第一定律特点：系统对外界所作的功以内能减少为代价。2、绝热过程方程\n绝热过程曲线的斜率等温过程曲线的斜率绝热线的斜率大于等温线的斜率.常量常量常量3、绝热过程曲线绝热线比等温线陡。证明:\n等容等压等温绝热总结:欲求W，Q或ΔE，要会用状态方程求出P、V、T过程方程\n例:设有5mol的氢气,最初的压强为温度为,求在下列过程中,把氢气压缩为原体积的1/10需作的功:1）等温过程.2）绝热过程.3）经这两过程后,气体的压强各为多少？解1）等温过程2）绝热过程12常量由得：3）等温过程绝热过程\n可用P-V图上一条有方向的闭合曲线表示。13－5循环过程卡诺循环一、循环过程1、定义：2、循环过程的分类OpV逆３、内能的变化、功、热量：内能变化：吸收的热量：正\n经历一个循环后对外作的净功气体对外所作的净功为：等于闭合曲线所包围的面积正循环取正号,逆循环取负号。\n求Ｗ或Ｑ的方法：②求得Qi，然后代数和即为Ｑ或Ｗ法二：循环过程分为几个小过程，对每一个小过程用第一定律③求得Qi，将所有正的相加为Q1，表示循环过程吸热;所有负的相加取绝对值（或负号）为Q2，表示循环过程放热。则有法一：Ｐ--Ｖ图上闭合曲线包围的面积带上正负号。AB①求得Ｗi，然后代数和即为Ｗ或Ｑ;\n热机（正循环）AB2、热机效率：表示热机的效能。热机热机示意图二、热机和制冷机1、热机：如蒸汽机、内燃机低温热源高温热源\n求热机效率：法一：用第一定律求得Qi,所有正的相加为Q1，所有负的相加取绝对值为Q2，例1、1mol氦气经过如图所示的循环过程，其中P2=2P1，V4=2V1，求：(1)1—2、2—3、3—4、4—1各过程中气体吸收的热量;(2)热机的效率1423\n1423解:（1）由理想气体状态方程得（2）或：（）\n练习：0.32kg的氧气作如图所示的ABCDA循环,设求循环效率K2002=TK3001=T解：M()21mV,-=TTCMmDADAD=EQ()ln121ABVVRTMmQ=()ln212VVRTMmCD=QBCBCD=EQ()21mV,-=TTCMm=1000CV,m>0=-1000CV,m<0=2000Rln1/2<0=3000Rln2>0%15=\nABCDPV0V1V4V2V3T1T2p1p4p2p3QABQCDAB：等温T1膨胀例、求卡诺热机效率。卡诺循环：四个过程如下图BC：绝热膨胀CD：等温T2压缩DA：绝热压缩\n效率：BC过程DA过程两式比较结论：卡诺热机的效率由高温热源和低温热源的温度决定，高温热源温度越高，低温热源温度越低，则循环效率越高；ABCDPV0V1V4V2V3T1T2p1p4p2p3Q1Q2\n例：一卡诺热机的低温热源温度为7℃，效率为40％，若要将其效率提高到50％，问高温热源的温度需提高多少？则有：T2=273.15+7=280.15K121TT¢¢-=¢¢h12,1TT¢-=¢h解：设高温热源的温度分别为:、1T¢1T¢¢K3.931111211=¢--¢¢-=¢-¢¢=DTTTThh\nAB4.致冷系数：致冷机致冷机示意图３.致冷机它是利用外界做功使热量由低温处流入高温处，从而获得低温的机器。低温热源高温热源表示致冷机的效能。\n卡诺制冷机：逆循环致冷系数T2ABCDPV0V1V4V2V3T1p1p4p2p3Q1Q2致冷机低温热源高温热源\n二、摩尔热容一、理想气体的物态方程总结三、理想气体的内能过程方程\n四、热力学第一定律理想气体准静态过程等容等压等温绝热欲求W，Q或ΔE，要会用状态方程求出P、V、T过程方程\n1、热机效率（或循环效率）五、热机和制冷机2.致冷机致冷系数：热机低温热源高温热源致冷机低温热源高温热源作业:P255-25813-1,2,3,5,13,14,18,23,25\n帕斯卡尔(BLAISEPASCAL)，1623～1662，法国17世纪最具天才的数学家、物理学家、哲学家。他在理论科学和实验科学两方面都做出巨大贡献。帕斯卡没有受过正规的学校教育但在他短短的39年人生里,干了很多的事情,哪一件都很了不起。他提出了几何学上的帕斯卡尔六边形定理、帕斯卡尔三角形，物理学上的帕斯卡尔定理等,他创制了世界上第一台计算机,他制作了水银气压计,他还是概率的创立人之一……科研和读书的间隙,他把他的思绪随时写在大页纸上,然后有一天,他把这些纸裁成小条,按内容归纳排列成书,这就是哲学名著《帕斯卡尔思想录》。在《思想录》里，留给世人一句名言：“人只不过是一根芦苇,是自然界最脆弱的东西，但他是一根有思想的芦苇.”他建立的直觉主义原则对于后来一些哲学家，如卢梭和伯格森等都有影响科学界铭记着帕斯卡的功绩，国际单位制规定“压强”单位为“帕斯卡”，是因为他率先提出了描述液体压强性质的“帕斯卡定律”。计算机领域更不会忘记帕斯卡的贡献，1971年面世的PASCAL语言，也是为了纪念这位先驱，使帕斯卡的英名长留在电脑时代里\n开尔文(1824—1907)是英国著名物理学家、发明家，原名W.汤姆孙。他是本世纪的最伟大的人物之一，是一个伟大的数学物理学家兼电学家。他被看作英帝国的第一位物理学家，同时受到世界其他国家的赞赏。他的一生获得了一切可能给予的荣誉。而他也无愧于这一切，这是他在漫长的一生中所作的实际努力而获得的。这些努力使他不仅有了名望和财富，而且赢得了广泛的声誉。开尔文研究范围广泛，在热学、电磁学、流体力学、光学、地球物理、数学、工程应用等方面都做出了贡献。他一生发表论文多达600余篇，取得70种发明专利，他在当时科学界享有极高的名望，受到英国本国和欧美各国科学家、科学团体的推崇。他在热学、电磁学及它们的工程应用方面的研究最为出色。开尔文一生谦虚勤奋，意志坚强，不怕失败，百折不挠。在对待困难问题上他讲：“我们都感到，对困难必须正视，不能回避；应当把它放在心里，希望能够解决它。无论如何，每个困难一定有解决的办法，虽然我们可能一生没有能找到。”他这种终生不懈地为科学事业奋斗的精神，永远为后人敬仰。1896年在格拉斯哥大学庆祝他50周年教授生涯大会上，他说：“有两个字最能代表我50年内在科学研究上的奋斗，就是‘失败’两字。为了纪念他在科学上的功绩，国际计量大会把热力学温标（即绝对温标）称为开尔文（开氏）温标，热力学温度以开尔文为单位，是现在国际单位制中七个基本单位之一。　　开尔文的一生是非常成功的，他可以算作世界上最伟大的科学家中的一位。他于1907年12月17日去世时，得到了几乎整个英国和全世界科学家的哀悼。他的遗体被安葬在威斯敏斯特教堂牛顿墓的旁边。\n摄耳修斯(1701～1744年)瑞典物理学家。在物理学中的主要贡献是建立了摄氏温标，也叫做百分温标。1742年他写了一篇论文《温度中两个不动刻度的观察》，受到广泛的重视。摄耳修斯把水的冰点和沸点作为固定点，还引入百分刻度法，水的沸点定作0°，冰点定作100°,这和现代摄氏温标的数序正好相反。几年以后，摄耳修斯的同事施勒默尔建议，把这个温标倒过来，冰点定作0°，水的沸点定作100°。1747年，奥普萨拉天文台就采用了摄耳修斯的温标。以后这一温标几乎被科学界普遍采用。开始人们称它是“瑞典温度”，大约在1800年，人们才称它是摄氏温度计。现在书写摄氏温度的时候，都在数值后面加上℃，读作“摄氏度”。这样，冰点和沸点分别记作0℃和100℃