大学物理 电势 35页

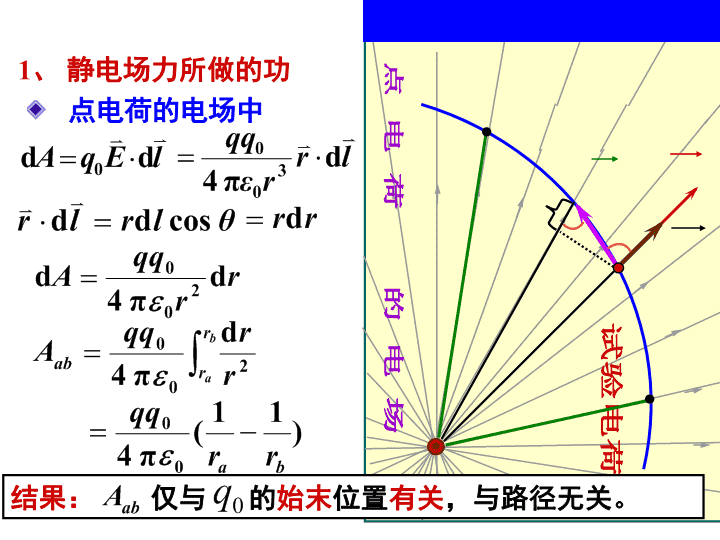
7.4静电场力的功电势\n静电场的性质：1）电荷在电场中受到电场力2）当电荷在电场中移动时，电场力要对电荷作功。电场强度电势先从库仑定律和场强叠加原理出发，证明静电场力的功与路径无关，说明静电场是保守场，然后引入描述静电场的另一个物理量——电势。一、静电场的环路定理\n试验电荷点电荷的电场无穷小1、静电场力所做的功点电荷的电场中结果：仅与的始末位置有关，与路径无关。\n任意带电体的电场（视为点电荷系）中结论：试验电荷在任何静电场中移动时，静电场力所作的功，仅与试验电荷的电量、起始与终了位置有关，而与路径无关。abL••\n2、静电场的环路定理12（CircuitalTheoremofElectrostaticField）静电场中，场强沿任意闭合环路的线积分恒等于零。静电场力是保守力，静电场是保守场。\n不是静电场！说明：2）环路定理要求电场线不能闭合。3）环路定理反映了静电场是保守场（或叫无旋场），可引入电势能的概念。abcd1）环路定理是静电场的另一重要定理，可用环路定理检验一个电场是不是静电场。\n静电场是有源、无旋（保守）场静电场是保守场静电场是有源场（或无旋场）静电场的高斯定理：静电场的环路定理：静电场的两条基本定理：无旋场\n二、电势差与电势静电场是保守场，静电场力是保守力。静电场力所做的功就等于电荷电势能增量的负值。电势能的大小是相对的，电势能的差是绝对的。1、电势能(ElectricPotentialEnergy)\n令试验电荷在电场中某点的电势能，在数值上等于把它从该点移到零势能处静电场力所作的功。电势能的参考点选择是任意的，则电场中A点的电势能为：若取b点为电势能的零点（零势点），即：\n例：若选择无限远处为电势能零点，试验电荷q0在点电荷q的电场中，A点处的电势能为：\n(积分大小与无关，反映了电场在a、b两点的性质。)2、电势电势差称为a、b两点的电势差。意义：把单位正电荷从A点沿任意路径移到B点的过程中，静电场力所做的功。\n电势差注意：电势差是绝对的，电势大小是相对的，与电势零点的选择有关。为了确定a点的电势值，可以选定b点的电势值为零，则a点的电势值为：令电场中某点的电势等于将单位正电荷从该点经任意路径移到零势点时电场力所作的功；也等于单位正电荷在该点的电势能。\n物理意义把单位正试验电荷从点Ａ移到无穷远时，静电场力所作的功。对有限带电体一般选无穷远为电势零点。对无限带电体不宜选无穷远为电势零点，只能选有限区域的某一位置为电势零点。在实际问题中，常选地球或仪器外壳的电势为零。电势零点的选择：（选无穷远为电势零点）（选P0为电势零点）\n电势差静电场力的功当已知电势分布时，可用电势差求出点电荷在电场中移动时电场力所做的功。公式小结：\n（1）点电荷电场中的电势电势的计算&取无穷远为电势零点，由定义式有drrPq3、电势叠加原理\n（2）电势叠加原理点电荷系表明：一个点电荷系的电场中任一点的电势，等于每一个点电荷单独存在时在该点所产生的电势的代数和。这一结论称作电势叠加原理。\n电荷连续分布带电体电场中的电势第一种方法：将带电体分为许多电荷元dq(点电荷)，利用点电荷的电势公式积分:第二种方法：按电势的定义式进行计算：学习重点：熟练掌握求电势、电势差及电场力的功的方法。（用高斯定理求电场）&（场强积分法）（电势叠加法）\n电势计算的两种方法：已知场强分布，由电势的定义式计算。（1）场强积分法（2）电势叠加法已知电荷分布，由点电荷的电势公式和电势叠加原理计算。（利用了点电荷电势公式。这一结果已选无限远处为电势零点，即使用此公式的前提条件为有限大带电体且选无限远处为电势零点。）当带电体为无限大模型时，只能用该定义计算！注意电荷元的选取！\n例1：一均匀带电圆环，已知：R、q。求：轴线上的电势分布解：方法一：点电荷电势+电势叠加原理\n方法二：场强积分法由电场强度的分布\n讨论\n（点电荷电势）均匀带电薄圆盘轴线上的电势\n例2：半径为R、总电量为q的均匀带电球面。求：电势分布。解：由高斯定理求出其场强分布:选定无限远处的电势为零，由电势的定义式，有：rR:rR:Rq\n方法二：叠加法(微元法)任一圆环由图\n例3：已知电荷q均匀地分布在半径为R的球体上，求：空间各点的电势。解：由高斯定理可求出电场强度的分布（方向沿径向）当r>R时：当r≤R时：\n例：“无限长”带电直导线的电势。解：令能否选？\nPdLq例4：一均匀带电直线段，长为L，电量为q；取无穷远为电势零点。求：直线延长线上离一端距离为d的P点的电势。解：将带电直线分为许多电荷元dq，利用点电荷电势公式积分：xdxdq\n解：（1）根据电势迭加原理例5：在正方形四个顶点上各放置带电量为+q的四个点电荷，各顶点到正方形中心O的距离为r。求：1）O点的电势；2）把试探电荷q0从无穷远处移到O点时电场力所作的功；3）电势能的改变。\n（2）根据电势差的定义（3）根据例5：在正方形四个顶点上各放置带电量为+q的四个点电荷，各顶点到正方形中心O的距离为r。求：1）O点的电势；2）把试探电荷q0从无穷远处移到O点时电场力所作的功；3）电势能的改变。\n例6：一带电球体，半径R，电荷体密度为=Ar，A为常量；求:球内外的电场和电势。Rrdr解：(1)电场rR:\n(2)电势rR:例6：一带电球体，半径R，电荷体密度为=Ar，A为常量；求:球内外的电场和电势。Rrdr\n例7：电荷以相同的面密度均匀分布在两个半径分别为R1=10cm、R2=20cm的同心球面上，设无穷远处为电势零点，已知球心电势为300v，求:1）=?2）空间电势分布；3）两球面的电势差。解：1）设内外球面分别带电q1和q2,应当指出，电势是空间坐标的连续函数。而电场一般是不连续的。R1R2oq1q2球心电势可用带电球面的电势叠加得出：\nq1=.4R12q2=.4R22球心电势也可用电势定义求得:于是得R1R2oq1q2\n(2)各区域电势：rR1:R1rR2:rR2:R1R2oq1q2\n(3)两球面的电势差:或R1R2oq1q2