大学物理干涉 134页

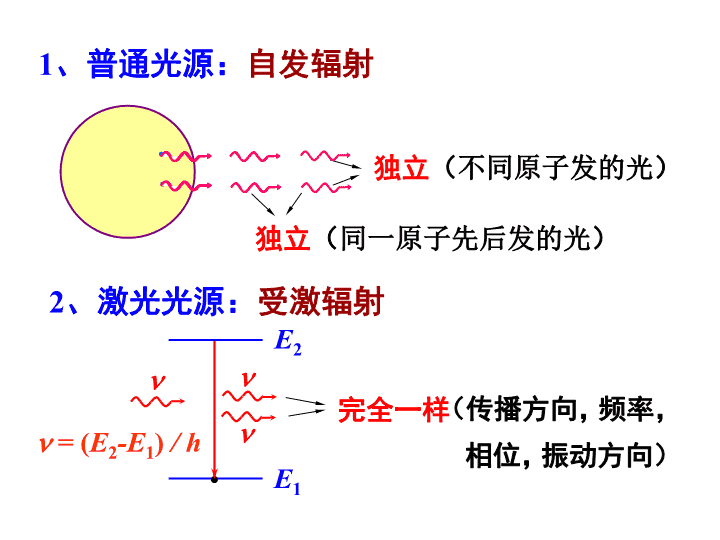
22.1光的相干性22.2双缝干涉及其他分波面干涉实验22.3时间相干性22.4空间相干性22.5光程22.6薄膜干涉（一）—等厚条纹22.7薄膜干涉（二）—等倾条纹22.8迈克耳孙干涉仪22.干涉\n22.1光的相干性一、光源（lightsource）光源发光，是大量原子、分子的微观过程。=(E2-E1)/hE1E2能级跃迁辐射波列波列长L=c能级、跃迁、辐射、波列持续时间～10－8s\n2、激光光源：受激辐射=(E2-E1)/hE1完全一样E21、普通光源：自发辐射··独立（同一原子先后发的光）独立（不同原子发的光）（传播方向，频率，相位，振动方向）\n(对时间平均)两束光叠加，相干和不相干二、光的相干性1、两列光波的叠加\n记为I=I1+I2+I12I1、I2分别是二光各自单独存在时的光强，叫做干涉项(可正可负)若各处都有I12=0，则I=I1+I2，不发生干涉。若I120，则II1+I2，干涉。关于干涉条件：假如各处＝以后讨论的多数情形有(或近似有)，合成时可当作标量波处理。\n设为简谐波，但频率不同。当作标量波，长时间内E1E2=0。频率不同的两光不能干涉。设同频率S1S2Pr1r2干涉项\n可当作标量波时，两列同频率的简谐波(理想单色波)总能干涉。但是，实际光波不是理想单色波。普通光源，发光机制，随机过程，一原子一次发光持续时间10－8s，一束光是大量原子发的光的总合，维持确定初相的时间10－8s。简化模型：实际光波的振幅、相位都迅速随机改变。相位随机迅变(取0－2间各值机会均等)。二独立光源S1、S2，10和20无联系，于是在观测时间内随机改变了很多很多次，使得振幅稳定，\n两束准单色光，同频率：有确定的相位关系，称为相干的(coherent)如果振动方向相同，可按标量波处理，就有(完全)相干叠加相位差极度混乱(随机迅变)不相干的I=I1+I2(incoherent)非相干叠加实际上有时介于相干与不相干之间，称为部分相干。\n产生干涉的必要条件频率相同存在相互平行的振动分量相位差稳定\n非相干光：I=I1+I2—非相干叠加完全相干光：相长干涉（明）（k=0,1,2…）相消干涉（暗）(k=0,1,2…)\n干涉相长Constructiveinterference\n干涉相消Destructiveinterference\n电磁波的干涉FlutteringTVpictures\nI02-24-44I1衬比度差(V<1)衬比度好(V=1)振幅比，决定衬比度的因素：光源的宽度光源的单色性，IImaxImin02-24-4干涉条纹可反映光的全部信息（强度，相位）2、条纹衬比度（对比度，反衬度，contrast）\n3、由普通光源获得相干光的途径PS*分振幅法：·P薄膜S*两束相干光在P点相干叠加分波面法：为了有稳定的相位差，应从同一点光源发的光分出二束，经不同路径后再相遇而叠加。常见的有两种方法：\n杨氏实验1801年，T.Young（1773-1829）22.2双缝干涉及其他分波面干涉实验\n两个点源的干涉两列球面波的干涉场设在均匀煤质中有两个作同频简谐振动的相干点波源S1和S2，其间距为d，它们各自向周围媒质发出球面波。考察空间任意一点P的光强。等强度点的轨迹是以S1和S2为焦点、并以其连线为轴线的双叶旋转双曲面。\n什么实验最美?2002年5月物理杂志PhysicsWorld上一位科学哲学家克里塞(Crease)提出一个问题：“物理学中最美的实验是什么?”到9月份，汇总200多位读者投票的结果，前10名按名次排列如下：\n1.用单电子做的杨氏双缝干涉实验(1961)2.伽利略的落体实验(1600左右)3.密立根油滴实验(1909)4.牛顿用棱镜将日光分解为七色的实验(1665-1666)5.杨氏用光做的干涉实验(1801)6.卡文迪许用扭杆测定万有引力常量的实验(1798)7.埃拉托色尼用阳光测定地球周长的实验(约公元前300)8.伽利略的斜面实验(1600左右)9.卢瑟福用粒子散射发现原子核的实验(1911)10.傅科摆的实验(1851)\nr1r2xdxD0单色光入射d>>，D>>d（d10-4m，D1m）光程差：相位差：P·一、双缝干涉\n明纹：暗纹：条纹间距：x0xIxr1r2xdxD0P·\n二、双缝干涉光强公式设I1=I2=I0，则光强为光强曲线k012-1-2I02-24-44I0sin0/d-/d-2/d2/dx0x1x2\n白光入射的杨氏双缝干涉照片红光入射的杨氏双缝干涉照片\nS，S1，S2是相互平行的狭缝Young’sdouble-slitexperiment\n\nyx\nThefringepattern\n例1白色平行光垂直入射到间距为d=0.25mm的双缝上，距缝50cm处放置屏幕，分别求第一级和第五级明纹彩色带的宽度。（设白光的波长范围是从400.0nm到760.0nm）。\n解:\n（1）一系列平行的明暗相间的条纹；（3）中间级次低，两边级次高明纹：k，k=0,1,2…（整数级）暗纹：(2k+1)/2（半整数级）（4）三、双缝干涉条纹的特点（2）不太大时条纹等间距；白光入射时，0级明纹中心为白色（可用来定0级位置），其余级明纹构成彩带，第2级开始出现重叠（书p.6例22.1）级次：k=\n四、干涉问题分析的要点（1）确定发生干涉的光束；（2）计算波程差（光程差）；（4）求出光强公式、画出光强曲线。（3）明确条纹特点：形状、位置、级次分布、条纹移动等；\n例2两束相干平行光同时照射在z=0的平面上。设两束光的波长为，振幅分别为A1和A2，在坐标原点处的初相位均为零，传播方向与xz平面平行，与z轴的夹角分别为1和2。求xy平面上干涉条纹的形状和间距。12\n解：12沿波传播方向每增加的距离，相位落后2。\n结果表明，亮纹位置只与x有关，而与y无关，因而干涉条纹是与y轴平行的直条纹。\n五、其他分波面干涉实验要求明确以下问题：1、如何获得的相干光；2、明、暗纹条件；3、干涉条纹特点：4、劳埃德镜实验，半波损失。形状、间距、级次位置分布；\n菲涅耳双面镜Fresnel’sdoublemirror\n菲涅耳双棱镜Fresneldoubleprism\n掠入射，产生了相位变化（半波损失）劳埃德镜Lloydmirror\n劳埃德镜\n反射相位突变问题有时要将反射光线偏振态与入射光线偏振态直接地作比较，以便确定反射光和入射光叠加的干涉场，由此提出反射相位是否突变的问题。光在界面的入射点也是反射点。当反射光在入射点的线偏振态与入射光的线偏振态恰巧相反，这表明界面反射有了相位突变，也称之为有半波损；若两者的线偏振态恰巧一致，这表明界面反射无相位突变，即没有半波损。这一表述本身已隐含着这样一个事实反射光p(s)振动与入射光p(s)振动方向是在一条直线上，这只有两种情况，正入射和掠入射，否则像斜入射那样，虽然两者的s振动是在一条直线上，但两者的p振动不在一条直线上，所谓“相反”或“一致”已经失去意义，这时应按实际需要作具体的针对性分析。●s●p’S’p\n在正入射的情况下，光从光疏介质到光密介质时反射光有半波损失，从光密介质到光疏介质时反射光无半波损失。在掠入射的情况下，无论光从光疏介质到光密介质，还从光密介质到光疏介质时，反射光均有半波损失。在任何情况下透射光都没有半波损失。可以证明：\n光从光疏介质到光密介质垂入射时反射光有的相位变化n1n2n1n2n1n2\n掠入射反射光有的相位变化\n例3如图所示，劳埃德镜的镜长C=5.0cm，幕与镜的右侧边缘相距B=3.0m，线光源S与镜的左侧边缘之间的位置关系已在图中示出，其中A=2.0cm,h=0.5mm,所用单色光的波长为=589.3nm，试求幕上干涉条纹的间距。幕上能出现多少根干涉条纹？\n解：产生干涉的两个光波可看成是从光源S与S的镜像S’发出的，发生干涉的区域为MN。OMF相似于S’DFONE相似于S’DE条纹间距为\n如果O点有光的干涉，由于半波损失O点为暗条纹。ON段的暗条纹数为OM段的暗条纹数为MN段的暗条纹数为\n例4一微波检测器安装在湖滨高出水面0.5m处。当一颗发射波长为21cm单色微波的射电星体徐徐自地平线升起时，检测器指出一系列信号强度的极大和极小。当第一个极大出现时，射电星体相对地平线的仰角为多少？解：采取直接计算光程差的办法求解。令(第一次出现相干极大)，得\n本题也可用其他方法求解，说明如下。(1)将星体和星体对湖面成的像看作两相干点源，于是可以照搬杨氏干涉装置。但双孔间距d和双孔到接收屏的距离D不知，可以灵活地将这两个未知量转化为用的函数表示。dD\n(2)星体离地面很远，入射到湖面的光为平行光，反射光也为平行光，因此这是两束平行光的干涉。无论采用哪一种方法，反射半波损都必须考虑。12本题中\n一、光的非单色性1、理想的单色光2、实际光束：波列准单色光22.3时间相干性（temporalcoherence）波列长L=c00II0:谱线宽度准单色光：在某个中心波长（频率）附近有一定波长（频率）范围的光。\n（1）自然宽度EjEiEi3、造成谱线宽度的原因（2）多普勒增宽（3）碰撞增宽·Ej\n例5杨氏实验装置中，采用加有蓝绿色滤光片的白光光源，波长范围为=100nm，平均波长为=490nm.试估算从第几级开始，条纹将变得无法分辨。，则按题意有相应于1和2，杨氏干涉条纹中k级极大的位置分别为：因此，k级干涉条纹所占据的宽度为解:设该蓝绿光的波长范围为\n显然，当此宽度大于或等于相应于平均波长的条纹间距时，干涉条纹变得模糊不清。这个条件可以表达为≥k≥所以，从第五级开始，干涉条纹变得无法分辨。\n另一方面，如图所示，当波长为(+)的第kM级亮纹中心，与波长为的第(kM+1)级亮纹中心重合时，即当时，总的干涉条纹的可见度降为零。实际上，这就是亮纹宽度x等于条纹间距x的条件。由此可以确定干涉条纹可见度降为零时的干涉级为与该干涉级kM对应的光程差M，就是实现相干的最大光程差，即.\n二、非单色性对干涉条纹的影响设能产生干涉的最大级次为kM，又则有-(/2)合成光强x1234560123450I0II0+(/2)\n三、相干长度与相干时间1、相干长度（coherentlength）两列波能发生干涉的最大光程差叫相干长度。：中心波长SS1S2c1c2b1b2a1a2·PS1S2Sc1c2b1b2a1a2P·才能发生干涉。波列长度就是相干长度：相干长度能干涉不能干涉只有同一波列分成的两部分，经过不同的路程再相遇时，\n\n普通单色光：激光：（实际上，一般为10-1101m）（理想情况）\n光通过相干长度所需时间叫相干时间。2、相干时间（coherentlength）的长短来衡量的。光的单色性好，相干时间时间相干性也就好。时间相干性的好坏，就是用相干长度δM（波列长度）或相干时间（波列延续时间）相干长度和相干时间就长，\n\n22.4空间相干性（spatialcoherence）一、空间相干性的概念光源宽度对干涉条纹衬比度的影响S1d/2S2RD光源宽度为bb/2LMN0M0N0LI非相干叠加+1L1NxI合成光强Ix合成光强b增大\nxI合成光强0Nx+1L0M0L-1NS1d/2S2RD光源宽度为b0b0/2LMN0M0N0LI非相干叠加+1L1N二、极限宽度当光源宽度b增大到某个宽度b0时，纹刚好消失：干涉条\n干涉条纹的移动造成条纹变动的因素：光源的移动装置结构的变动光路中介质的变化\n例6在双缝干涉实验中，若单色光源S到两缝S1S2距离相等，则观察屏上中央明条纹位于图中O处，现将光源S向下移动到示意图中的S位置，则：（A）中央明条纹也向下移动，且条纹间距不变；（B）中央明条纹向上移动，且条纹间距增大；（C）中央明条纹向下移动，且条纹间距增大；（D）中央明条纹向上移动，且条纹间距不变。[D]\n例7在杨氏双缝干涉的实验装置中，入射光的波长为。若在缝S2与屏之间放置一片厚度为d、折射率为n的透明介质,试问原来的零级亮纹将如何移动？如果观测到零级亮纹移到了原来的k级亮纹处，求该透明介质的厚度。解：在缝S2与屏幕之间放置了透明介质片之后，从S1和S2到屏幕上的观测点P的光程差为零级亮纹相应于，其位置应满足(1)\n与原来零级亮纹位置所满足的r2-r1=0相比可以看出，在放置介质片之后，零级亮纹应该下移。在没有放置介质片时，k级亮纹的位置满足(2)按题意，在放置了介质片之后，观测到零级亮纹移到了原来的k级亮纹处。因此式(1)和式(2)必须同时得到满足，由此可解得其中为k负整数。上式也可以理解为，透明介质片的插入使屏幕上的杨氏干涉条纹移动了这提供了一种测量透明介质折射率的方法。条。\n光源的移动所引起的干涉条纹的移动当位于对称轴上的点光源沿y方向移动时，干涉条纹不变；当它沿x方向移动时，条纹将沿x轴上下移动。xyS1S2z\n\n光源宽度对干涉条纹衬比度的影响\nδs→δx,b2→Δx/2,b0→Δx点源位移条纹位移\n为观察到较清晰的干涉条纹通常取dDR极限宽度b0时，才能观察到干涉条纹。当光源宽度当光源宽度b由很小的值逐渐增大到某个宽度b0时，干涉条纹刚好消失，b0称为光源的极限宽度。\n三、相干间隔和相干孔径角1、相干间隔R一定时，d0越大，光场的空间相干性越好。由则要得到干涉条纹，必须令—相干间隔d0bS1S2Rd若b和R一定，相干间隔d0是光场中正对光源的平面上能够产生干涉的两个次波源间的最大距离。\n2、相干孔径角S1S2b0d0R相干孔径角：0越大空间相干性越好。在θ0范围内的光场中，正对光源的平面上的任意两点的光振动是相干的。普通单色光源分波面干涉受到光源宽度的限制，不受以上限制。相干孔径角来代替。相干间隔也可以用—d0对光源中心的张角。存在条纹亮度和衬比度的矛盾。而激光光源则\n光场的空间相干性\nbn3，或n1>n2n2>n3，无相位突变12\n本节讨论不均匀薄膜表面的等厚条纹。一、劈尖（wedgefilm）干涉夹角很小的两个平面所构成的薄膜叫劈尖。1、2两束反射光来自同一束入射光，它们可以产生干涉。1、2两束反射光相干叠加，就可行成明暗条纹。ennn(设n>n)反射光2反射光1单色平行光\n反射光1单色平行光垂直入射ennn·A反射光2(设n>n)所以反射光1、2的明纹：暗纹：同一厚度e对应同一级条纹—等厚条纹实际应用中大都是平行光垂直入射到劈尖上。程差可简化计算。考虑到劈尖夹角极小，反射光1、2在膜面的光光程差为在A点，反射光1有半波损失，\n条纹间距：因此Leekek+1明纹暗纹nL\n\n等厚干涉条纹劈尖不规则表面\n白光入射单色光入射肥皂膜的等厚干涉条纹\n例10用劈尖干涉法可检测工件表面缺陷，当波长为的单色平行光垂直入射，若观察到的干涉条纹如图所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分：空气劈尖工件平面玻璃\n（A）凸起，且高度为/4；（B）凸起，且高度为/2；（C）凹陷，且深度为/2；（D）凹陷，且深度为/4。[C]空气劈尖工件平面玻璃\n例11两块平板玻璃构成一空气劈尖，长L=4cm，一端夹住一金属丝，如图所示，现以波长为=589.0nm的钠光垂直入射，（1）若观察到相邻明纹（或暗纹）间距离l=0.1mm，求金属丝的直径d=？（2）将金属丝通电，受热膨胀，直径增大，在此过程中，从玻璃片上方离劈棱距离为L/2的固定观察点上发现干涉向左移动2条，问金属丝的直径膨胀了多少？\n解：（1）相邻明纹间对应的厚度差为/2，如图所示。（2）在劈尖中部（距劈棱处），干涉条纹向左移两个条纹，说明在该处厚度增加2/2，因劈尖上表面不是在保持q不变情况下的平移，\n所以根据两个直角三角形的相似关系可知金属直径处增加2，即：\n(1)暗环erR·平晶平凸透镜o二、牛顿环(2)暗环：∴条纹间距，内圈的条纹级次低。（k=0，1，2…）(1)、(2)第k个暗环半径：光程差：很大\n明环半径公式（自己推导）牛顿环装置简图：平晶S分束镜M显微镜0平凸透镜.\n\n牛顿环照片\n白光入射的牛顿环照片\n三、等厚条纹的应用1、劈尖的应用测波长：已知θ、n，测L可得测折射率：已知θ、，测L可得n测细小直径、测表面不平度h待测块规标准块规平晶等厚条纹待测工件平晶待测样品石英环平晶干涉膨胀仪依据公式厚度、微小变化：（书p.19例22.4）（书p.19例22.5）\n2、牛顿环的应用：测透镜球面的半径R测波长检验透镜球表面质量标准验规待测透镜暗纹已知,测m、rk+m、rk，可得R。已知R，测出m、rk+m、rk，可得。依据公式若条纹如图，说明待测透镜球表面不规则，且半径有误差。一圈条纹对应的球面误差。\n暗纹标准验规待测透镜暗纹标准验规待测透镜如何区分如下两种情况?思考\n检测工件曲率半径扩大收缩\n例12如图，用单色光垂直照射在观察牛顿环的装置上，设其平凸透镜可以在垂直的方向上移动，在透镜离开平玻璃过程中，可以观察到这些环状干涉条纹。（A）向右平移；（B）向中心收缩；（C）向外扩张；（D）静止不动；（E）向左平移。单色光空气[B]\n例13.Whitelightisnormallyincidentonasoapfilmthathasaironbothsides.Thereflectedlightisorange.Ifoneassumesthattheindexofrefractionofthefilmis1.33andthat6000Angstromsisatypicalwavelengthoforangelightinair,apossiblethicknessofthefilmismostnearlyA.1500AB.3000AC.3375AD.4225AE.4500A解：考虑到半波损，橙色反射光干涉加强的条件为代入题中给出的数据，当i=1时，d=3375A。选（C）。四、增透射膜和增反射膜（书p.20,例22.6）\n一、点光源照明时的干涉条纹分析LfP0r环ennn>nrACD·21Siiii光束1、2的光程差：得·膜厚均匀（e不变）·又·B·22.7薄膜干涉（二）—等倾条纹（equalinclinationfringes）\n或明纹暗纹形状：条纹的特点：一系列同心圆环r环=ftgi条纹间隔分布：内疏外密（为什么？）条纹级次分布：内高外低波长对条纹的影响：膜变厚，环纹扩大：i相同的光线对应同一条干涉条纹—等倾条纹即倾角当k(k)一定时，i也一定，LfPor环iSi12en’nii·n’\n二、面光源照明时，干涉条纹的分析只要i相同，都将汇聚在同一个干涉环上（非相干叠加），因而明暗对比更鲜明。foennn>n面光源·Pr环·ii·\n观察等倾条纹的实验装置和光路inMLSf屏幕对于观察等倾条纹，没有光源宽度和条纹衬比度的矛盾!\n等倾条纹照片\n例14在如图所示的装置中，透镜焦距为f=20cm，光源波长为=600nm，产生干涉现象的薄膜是玻璃板（折射率ng=1.5）上的氟化镁涂层，其折射率为n=1.38，厚度为d=5.0010-2mm，试问(1)在反射光方向上观察到的干涉圆环，其中心是亮点还是暗点?(2)从中心向外计算，第5个亮环的半径是多少?inMLSf屏幕ngd解：(1)由于薄膜折射率介于空气和玻璃之间，所以两反射相干光间无附加光程差，中心点的光程差为\n可得由于是k0整数，因此中心点是亮点。(2)对于从中心向外的第N个亮环，其干涉级为由和可得再利用折射定律，以及小角度近似和可得第N个亮环的角半径和半径分别为：\n将N=5代入上式，可得从中心数第5个亮环的角半径和半径分别为：\n22.8迈克耳孙干涉仪（Michelsoninterferometer）一.仪器结构、光路二.工作原理光束2′和1′发生干涉若M1、M2平行等倾条纹若M1、M2有小夹角等厚条纹十字叉丝等厚条纹M12211半透半反膜补偿板反射镜反射镜光源观测装置薄膜则有：补偿板可补偿两臂的附加光程差。若M1平移d时，干涉条移过N条，SM2M1G1G2E\n补偿板补偿板在单色光照明时并非必要，光束2经过玻璃板所增加的光程，光束1可以用空气中的行程来补偿。但是当光源发出的光具有较大的频谱宽度时，因为玻璃有色散，不同波长的光有不同的折射率，因而对不同的波长，通过玻璃板时所增加的光程不同，这是无法用空气中的行程来补偿的，这时必须加入补偿板才能同时补偿各种波长的光程差。\n\n迈克耳孙干涉仪\n\n迈克耳孙在工作迈克耳孙（A.A.Michelson）因创造精密光学仪器，用以进行光谱学和度量学的研究，并精确测出光速，获1907年诺贝尔物理奖。美籍德国人\n全息照相实验、迈克耳孙干涉仪至今仍是许多光学仪器的核心。爱因斯坦赞誉道：“我总认为迈克耳孙是科学中的艺术家，最大乐趣似乎来自实验本身的优美的精湛，和所使用方法他从来不认为自己在科学上是个严格的‘专家’，事实上的确不是，他的但始终是个艺术家。”重要的物理思想＋巧妙的实验构思＋精湛的实验技术科学中的艺术许多著名的实验都堪称科学中的艺术，如：吴健雄实验、施—盖实验等等。\n三、迈克耳孙干涉仪的应用测介质折射率测量微小位移ln光路1中插入待测介质，由此可测折射率n。以波长为尺度，可精确到产生附加光程差：M11若相应移过N个条纹，则应有（书p.27习题22.23）\n用迈克耳孙干涉仪测气流\n第22章结束\n知识回顾KnowledgeReview祝您成功！