【精品】大学物理下册 40页

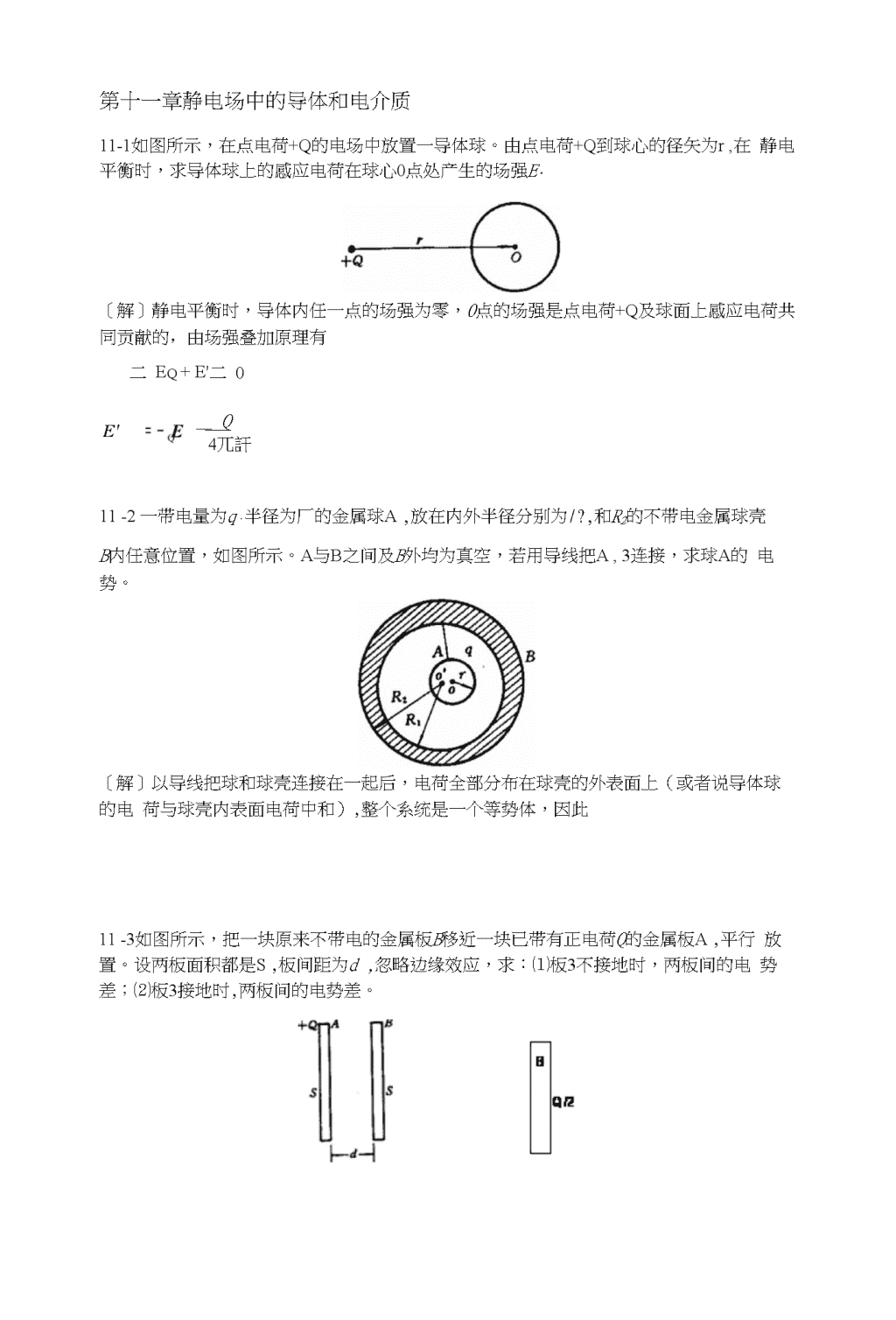
第十一章静电场中的导体和电介质11-1如图所示，在点电荷+Q的电场中放置一导体球。由点电荷+Q到球心的径矢为r,在静电平衡时，求导体球上的感应电荷在球心0点处产生的场强E。［解］静电平衡时，导体内任一点的场强为零，0点的场强是点电荷+Q及球面上感应电荷共同贡献的，由场强叠加原理有二Eq+E'二0E'__Q4兀訐211-2一带电量为q、半径为厂的金属球A,放在内外半径分别为/?,和R2的不带电金属球壳B内任意位置，如图所示。A与B之间及B外均为真空，若用导线把A,3连接，求球A的电势。［解］以导线把球和球壳连接在一起后，电荷全部分布在球壳的外表面上（或者说导体球的电荷与球壳内表面电荷中和）,整个系统是一个等势体，因此11-3如图所示，把一块原来不带电的金属板B移近一块已带有正电荷Q的金属板A,平行放置。设两板面积都是S,板间距为d,忽略边缘效应，求：⑴板3不接地时，两板间的电势差；⑵板3接地时,两板间的电势差。\n［解］⑴由61页例1知，两带电平板导体相向面上电量大小相等符号相反,而相背面上电量大小相等符号相同，因此当板B不接地，电荷分布如图因而板间电场强度为E二22JS电势差为UAli=Ed=Qd2JS⑵板B接地时，在B板上感应出负电荷，电荷分布为-Q0故板间电场强度为E二2电势差为+世11-4如图所示，有三块互相平行的导体板，上导体板到中间导体板的距离为5.0cm,上导体板到下导体板的距离为8.0cm，夕湎的两块用导线连接，原来不带电。中间一块两面上带电,其面电荷密度之和为a二1.3Xn?。求每块板的两个表面的面电荷密度各是多少（忽略边缘效应）？［解］因忽略边缘效应,可把三个导体板看作无限大平板,由例1知\n忽略边缘效应，则导体板可看成无限大的，具有屏蔽性，在相邻导体板之间的电场只由相对于二表面上电荷决定。因此上板和中板之间的场强为\n在中板和下板之间的场强为G)上板和下板相连接，因此相邻两板的电势差相等，即EQ二E4.由此可得(J3〃1二。4〃2设中板总面电荷密度为(J则03^q二°由(3)、(4)两式可得CT3=8X10C/m2CT4=CT-(T3二5'6c/m2x10代入(1)、⑵两式中得到CT2=-8Xrdc/m2CT5=-5x_6C/m210在上板内任意点场强均为零，它是6个无限大均匀带电平面在该点产生的场强叠加的结果。故有—((T.-?-CT-a-(J-CT)=02812oa3456考虑到⑴、⑵两式，则得到CT,=CT6(5)上下两块导体板原来是不带电的，根据电荷守恒定律，二导体板表面出现感应电荷后，总量仍为零。因此有…b22526(6)二0由(5)、⑹两式得到:广一扌(q+j)°62二-扌X(-8X10-6一5X10_6)=6.5X10/6Cm211-5如图所示，三个无限长的同轴导体圆柱面久B和C,半径分别为&、心、«。圆柱面B上带电荷，A和C都接地。求B的内表面上线电荷密度A|和外表面上线电荷密度A2\n之比值心入2。\nRc［解］由久C接地L%由高斯定理知Ef_X27T8恥二广片d厂心27184c叮T心Mb2兀Edrz'2A,A。厂.RrIn—二心2因此11-6在一半径为R、=6.0cm的金属球A夕卜面套有一个同心的金属球壳B。已知球壳B的内、外半径分别为仏=&0皿，/?3=10.0cme设球4带有总电量2二3x10^C，球壳3带有总电量Q厂2x10弋。求：⑴球壳B内、夕卜表面上各带有的电量以及球A和球壳B的电势；(2)将球壳B接地然后断开,再把金属球A接地,求金属球A和球壳B内、夕卜表面上各带有的电量以及球A和球壳B的电势。［解］在球壳B内作一包围内腔的高斯面,由于球壳内场强处处为零，此高斯面的电通量为零。根据高斯定律，球壳B的内表面上所带电量与球A所带电量等值异号，所以^=-2a=-3xio-8c球壳B总电量为0,因此其外表面上电量为\n务外二Qb-%內二（2xi（r+3xi（r）c=5xi（rc球a的电势为\nQa347T§,+4X0/?2+47T£0■47T£0/?,R2R、,R8R,二9Xio9X5X1O'8jxl°〔+-3x1°：+—2V二5.63Xlow\6.0xIO-28.0xi(f210.0xiO-2/1u二Qa*qb内+%外"47T§47T80/?3u二久外=9x^x5x10-v=45x1()3vB4"3R10.0xi(f2因为Qa+务内二0，所以(2)将球壳B接地时，其电势变为零。因为与％内等量异号，它们在球壳B产生的电势之和为零，所以球壳外表面不再有电荷。球壳B与地断开后，再各球A接地时，电荷将重亲斤分布。设球A、球壳B内表面、球壳B外表面上电量分别为Q；、9：内、Q；外因为U=0,于是有fAqQa+B内'47TE,/+qb外二ol4兀£o47TE0R2注意这时仍有el十q；内二0,而且3-x^e—x-6t0^8.0C=2」2X1(T*C8.0x10.0-6.0x10.0+6.0x8.0\n=-2.12x10'8C0：金属球A接地’电势U二/1Qa+9b内+_企_外B4兀§47T847T厂o厂兀+2」2X1O_8)C=-8.8X1O'9C,球壳B电势为9-二务外04兀£尼\n9x109x8.8X10)V二-7.92x16V■910.0X10-211-7一厚度为d的无限大均匀带电导体板,单位面积上两表面带电量之和为CT。试求离左表面的距离为a的点与离右表面的距离为b的点之间的电势差。解］导体板内场强E内二0,由高斯定理可得板外场强为E-(J2E(J,CTOdx+Jdx二0C,故久B两点间电势差为Jia匕b二J®引二28A011-s半径分别为r｝和他（凡〉尺）的两个同心导体薄球壳,分别带电量e,和q2.今将内球壳用细导线与远处的半径为r的导体球相连,导体球原来不带电。求相连后导体球的带电量q。［解I整个系统仍是孤立球形电容G与内球到无限远（地）之间的电容之并联。而后者是内球形电容C.与外球孤立球形电容c2串联所构成的=47T£C?二4兀£0/?2C3=47T£or设小球C.上电量为「则C|上电量e,-q,C2上电量为Q2+(e,-q)设三个电容上的电压各\n2兀ErL27TErR2L8因£,二2.5E得到R2二2.57?,当£二&时电缆的电压最大。27(e0€rL&/二q/c.U{=(et-q}/C,U2=(e2+Q-(l)/c2由于—二5+U2所以厶giZ_J+2SqC3C］C2因而移到小球上的电量为r(/?20+&幺)qj11-9一种单芯同轴电缆的中心为一半径K=0.5cm的金属导线，其外层包一层「二5的固体电介质，最外面的是金属包皮。当在此电缆上加一电压后，介质中紧靠其内表面处的场强耳为紧靠其外表面处的场强色的2.5倍,若介质最大安全场强£二40kV/cm,求此电缆能承受的最大电压是多少？［解］由介质中的高斯定理d)32兀2£o4W-|K2。〈厂〈b)327T206rEr40(c/?2的区域为真空。设沿轴线单位长度上导线的带电量为儿，圆筒的带电量为・Ao,忽略边缘效应,求：(1)何处电场强度最大?其值为多少?(2)电容器两极间的电势差；(3)电介质区域的电场总能量。\n［解］⑴a