大学物理答案49437 11页

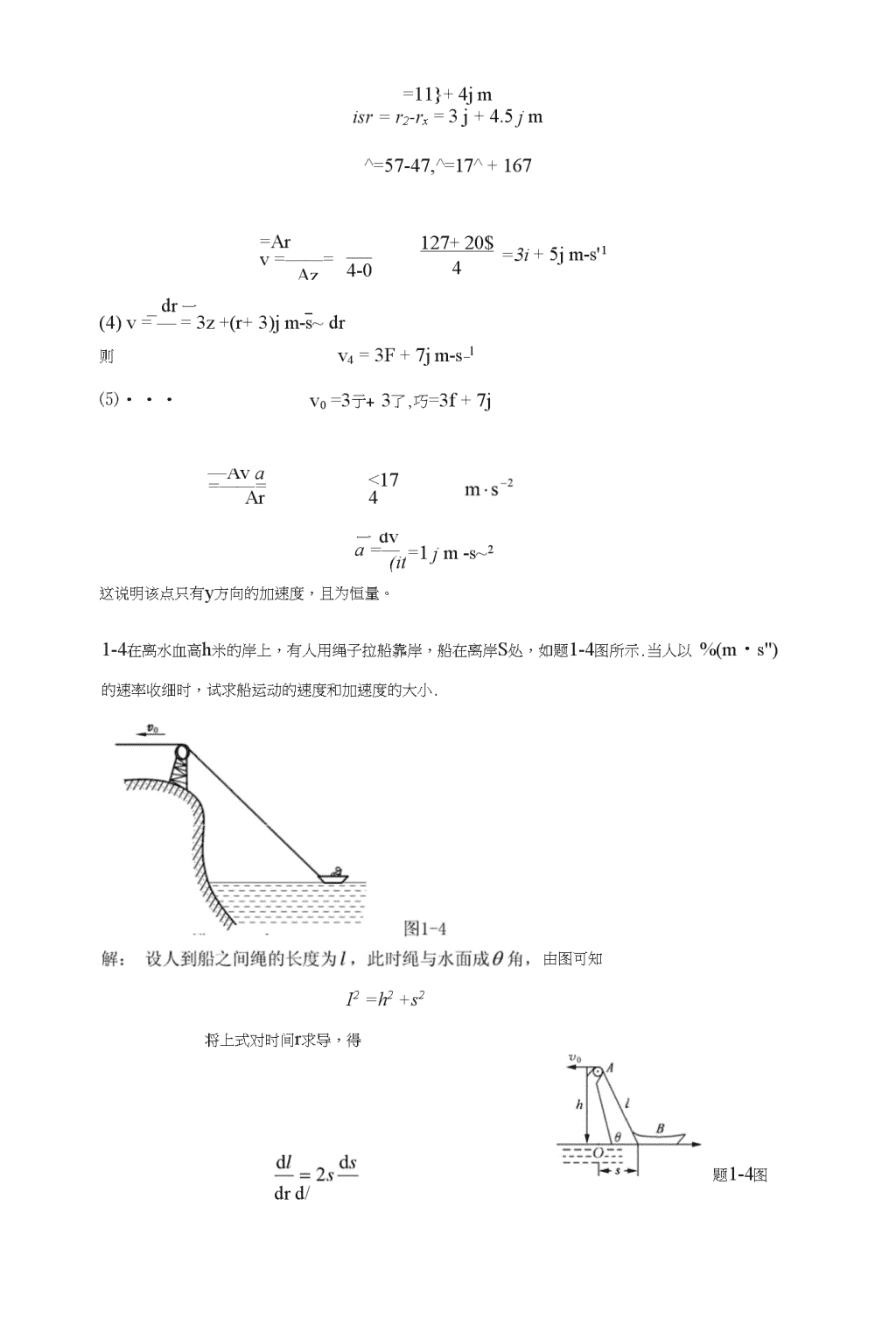
1-1IAr丨与zk有无不同？竺drAt习题解答习题一有无不同?dvdr和—有无不同?其不同在哪里?dt即|Ar|=|r2-rj,Ar试举例说明.解：（1）|Ar|是位移的模，△厂是位矢的模的增量,drdr(2)是速度的模，即dzdr=Vdsdz’只是速度在径向上的分量.drdtdr.dr—r+r一dtdtT有厂=rr（式中F叫做单位矢）,式中’就是速度径向上的分量，dr竺与竺不同如题1—1图所示.dtdt（3）宁表示加速度的模'即同曙不是加速度。在切向上的分量.V^v=vf（f表轨道节线方向单位矢），所以dvdv_dr—=—r+v——dzdrdr式小d就是加速度的切向分量.dtAAdFdt（・・・一与一的运算较复杂，超出教材规定，故不予讨论）drdr1-2设质点的运动方程为x=x（r）,y=y（r）,在计算质点的速度和加速度时，有人先求出Z、=J/+）,2,然后根据卩二屯，及a=^r而求得结果；又有人先计算速度和加速度d/d广的分量，再合成求得结果，即你认为两种方法哪一•种\n正确？为什么？两者差別何在？解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有r=xF+）7,一drdy=v=—=—i+—/drdrdr一d2rd2x.d2y.a—~—~i+~]dr2dr2dr2故它们的模即为而前一种方法的错谋可能冇两点，其一是概念上的错误，即误把速度、加速度定义作d2rdr7drv=—At其二，可能是将二与二误作速度与加速度的模。在1-1题中已说明二不是速度的模,drd厂dr而只是速度在径向上的分量，同样，卑也不是加速度的模，它只是加速度在径向分量屮dr212/4/Q\的一部分c%=^-r—0或者概括性地说，前一种方法只考虑了位欠r在径向（即_dr-1曲丿」量值）方面随时间的变化率，而没有考虑位矢戸及速度0的方向随间的变化率对速度、加速度的贡献。1-3一质点在兀Oy平而上运动，运动方程为1兀二3/+5,y=—t+3L4.2式中r以s计，小丿以皿计.（1）以时间f为变量，写出质点位置矢量的表示式；⑵求出21s时刻和t=2s时刻的位置矢量，计算这1秒内质点的位移；（3）计算t=0s时刻到f=4s时刻内的平均速度；（4）求出质点速度矢最表示式，计算f=4s时质点的速度；（5）计算f=Os至Ijr=4s内质点的平均加速度；（6）求岀质点加速度矢量的表示式，计算/=4s时质点的加速度（诘把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成宜角坐标系中的矢量式）.解：（1）F二⑶+5）亍+（丄+3f_4）jm2（2）将/=t=2代入上式即有斤=&一0.5丿m\n=11}+4jmisr=r2-rx=3j+4.5jm^=57-47,^=17^+167=Arv=——=Az4-0127+20$4=3i+5jm-s'1_dr一_(4)v=—=3z+(r+3)jm-s~dr则v4=3F+7jm-s_l⑸・・・v0=3亍+3了,巧=3f+7j—Ava=——=Ar<174一dva=—(it=1jm-s~2这说明该点只有y方向的加速度，且为恒量。1-4在离水血高h米的岸上，有人用绳子拉船靠岸，船在离岸S处，如题1-4图所示.当人以%(m・s")的速率收细时，试求船运动的速度和加速度的大小.由图可知I2=h2+s2将上式对时间r求导，得drd/题1-4图\n根据速度的定义，并注意到是随/减少的，d/dsd$1d/Iv0%=市=二矿%=如=4山将y船再对f求导，即得船的加速度sd//ds小dv船5drdr、，-vGs+lv船a=~^-=2—vo=；vodr5s[2(-$+—)评力22S_H豺0—3—-31-5质点沿x轴运动，英加速度和位置的关系为a=2+6x2,a的单位为m-s"2,x的单位为m.质点在兀=0处，速度为10m-s'1,试求质点在任何坐标处的速度值.解：•・•dvdvdxdva=—==v—drdrdrdx分离变量：auAv=adx=(2+6x\)dr两边积分得—v2=2x4-2x3+c2由题知，兀=0时，v0•••=10,・；c=50v=2a/x3+x+25m-s11-6已知一质点作直线运动，-其加速度为a=4+3rm•s~2,开始运动时，x=5m,v=o,求该质点在r=ios时的速度和位置.解：•・・dva=—=4+3fdr分离变最，得dv=(4+3r)dr积分，得v=4t+-t+q2山题知，r=0,v0=0q=0\n故又因为分离变量,积分得/3?v=4t+-t~2dr32v=一=4/+—/dr23dx=(4t+-r)dtr213X=2fH—t+c?2・\n故所以r=10s时卡+『+5=4xl0+-xl02=1902-im-sxio=2“+”+5=7051-7—•质点沿半径为lm的圆周运动，运动方程为0二2+3八，0式屮以弧度计，/以秒计,求：(1)t=2s吋，质点的切向和法向加速度；⑵当加速度的方向和半径成45°角吋，其角位移是多少？解：(1)f=2s时,a)=—=9t2^=—=18tdtdt=/?/?=1x18x2=36m-s~2an=R(o2=lx(9x22)2=1296ms-2(2)当加速度方向与半径成45°角时，有即亦即则解得于是角位移为tan45。=乞=1anRco2二Rp(9r2)2=18/92&=2+3厂=2+3x—=2.679rad由题知/=0,x0=5,c2=5\n1"1-8质点沿半径为/?的圆周按5=VQt-一价2的规律运动，式中$为质点离圆周上某点的弧2长，心，“都是常最，求：仃力时刻质点的加速度；(2)f为何值时，加速度在数值上等于b.解：(1)d$.v=—=v.-btdr0dt,(Vq-^)4R2加速度与半径的夹角为ciT—Rb(P=arctan—=rJ(v0-<(2)由题意应有b2,(Vq-^)4R2宀气竺—)'OK1-9以初速度v0=20m-s_1抛出一小球，抛出方向与水平面成a=60的夹角,求：(1)球轨道最高点的曲率半径⑵落地处的Illi率半径/?2・(提示：利川曲率半径与法向加速度之间的关系)解：设小球所作抛物线轨道如题1-9图所示.题1-9图(1)在最高点,\n乂•••P\v.2n\(2)在落地点,vt=vv=v0cos60°心i=10m-s-2=10mP\(20xcos60o)210v2=v0=20ms-1,(20)210xcos60°仏=gxcos60°=80ml・10飞轮半径为0.4m,自静止启动，其角加速度为0二0.2rad・s—2,求/=2s时边缘上各点的速度、法向加速度、切向加速度和合加速度.解：当r=2s时，e=0/=0.2x2=0.4rads-1则v=Rco-0.4x0.4=0.16m-s_1cin=Rco2=0.4x(0.4)2=0.064m•s"2aT=R/3=0.4x0.2=0.08m•s-2a=屁+d；=J(0.064)2+(0.08)2=0」02m-s-2i-ii如题i-ii图，物体A以相对B的速度v=沿斜面滑动，y为纵坐标，开始时人在斜而顶端高为力处，〃物体以"匀速向右运动，求A物滑到地面时的速度.解：当滑至斜而底时，y=h,则二J顽，A物运动过程中乂受到B的牵连运动影响,因此，A\n对地的速度为乙地=历+巧=(u+』2ghcosa)i+(』2ghsina)j\n1-12一船以速率v,=30km・2沿直线向东行驶，另一小艇在其前方以速率冬=40km・h"沿直线向北行驶，问在船上看小艇的速度为何?在艇上看船的速度乂为何？解：⑴大船看小艇，则有v2l=v2-vP依题意作速度矢量图如题1-12图(a)(a)(b)题1-12图由图可知v21=+必=50km•h1v.3方向北偏西0=arctan—=arctan—=36.87°v24(2)小船看人船，则有％2=歼-°2,依题意作出速度矢最图如题1T2图(b),同上法，得v12=50kmh_1方向南偏东36.87°1-13在河水流速心=2ms"1的地方有小船渡河.如果希望小船以u=4ms_,的速率垂直于河岸横渡，问小船相对于河水的速度大小和方向应如何？\n解：设小船相对于河水的速度方向如图示•U2=/+U：u=Ju?+uj=2V5m/s=4.47tan(O-90°)=乞=二=—u2逅50=114.09