大学物理科里奥利力 11页

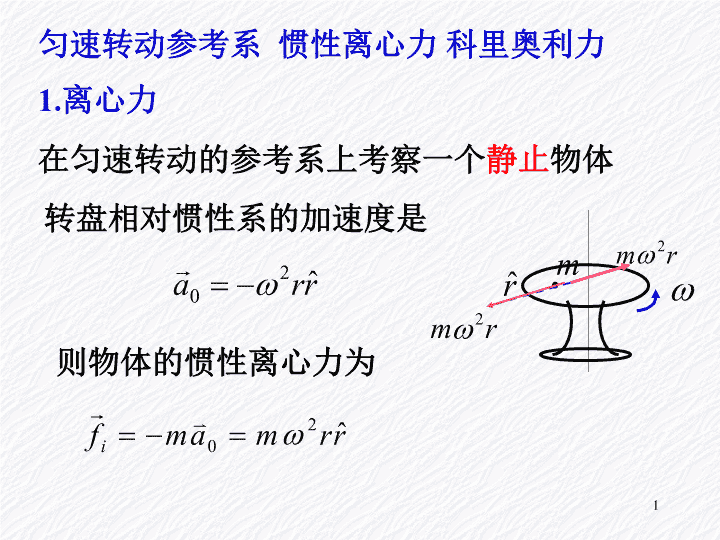
匀速转动参考系惯性离心力科里奥利力1.离心力在匀速转动的参考系上考察一个静止物体则物体的惯性离心力为转盘相对惯性系的加速度是1\n2.科里奥利力Coriolisforce相对转动参考系运动的物体，除受到离心力外，还受到一个力，称科里奥利力。表达式为：推导见后2\n1、科里奥利力的特征1）与相对速度成正比只有在转动参考系中运动时才出现2）与转动角速度一次方成正比当角速度较小时，科氏力比惯性离心力更重要3）科氏力方向垂直相对速度该力不会改变相对速度的大小4）科氏力在地球上的表现讨论科氏力：3\n北半球的河流水流的右侧被冲刷较重落体向东偏斜付科摆摆动平面偏转证明地球的自转北半球的科氏力信风的形成旋风的形成柏而定律图示4\n赤道附近的信风(北半球东北，南半球东南)5\n傅科摆▲傅科摆摆锤28kg，摆平面转动）顶视11223摆平面转动周期北京，巴黎，这是在地球上验证地球转动的著名的实验。（傅科，1851，巴黎伟人祠，摆长67m，地球摆实物演示科氏力6\n附：科里奥利力简单推导·rmω=const.S′SO光滑凹槽●如图，质点m在转动参考系（设为S'系）中沿一光滑凹槽运动，速度为我们以特例推导，然后给出一般表达式。7\n在惯性系（地面）S：在非惯性系（圆盘）S′：向心加速度，·rmω=const.S′SO光滑凹槽●8\n转换到非惯性系（圆盘）S′中使用：将惯性系（地面S）中的牛二定律式分析：---惯性离心力----科里奥利力惯性力9\n推广到一般表示式：首先引入角速度矢量科氏力：在非惯性系中牛二的形式角速度矢量方向：四指绕物体旋转方向，拇指的指向就是角速度的方向。10\n惯性力：则有：在非惯性系中，只要在受力分析时加上惯性力后，就可形式上使用牛顿定律。一般表示式：11