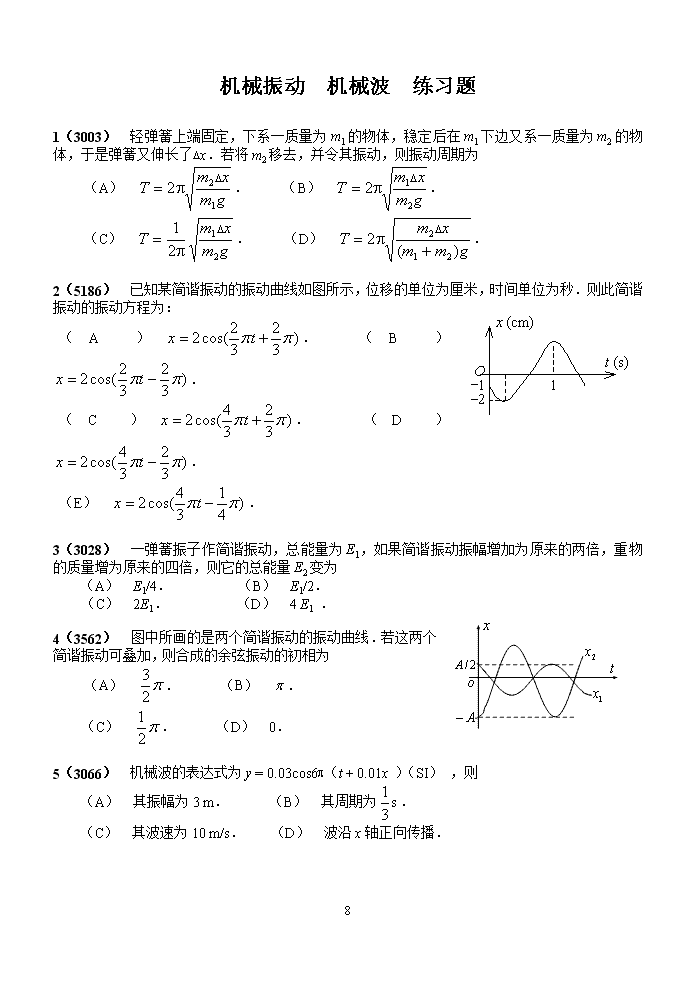大学物理习题7 4页

机械振动　机械波练习题1（3003）　轻弹簧上端固定，下系一质量为m1的物体，稳定后在m1下边又系一质量为m2的物体，于是弹簧又伸长了Dx．若将m2移去，并令其振动，则振动周期为（A）．（B）．（C）．（D）．2（5186）　已知某简谐振动的振动曲线如图所示，位移的单位为厘米，时间单位为秒．则此简谐振动的振动方程为：（A）．　（B）．（C）．（D）．（E）．3（3028）　一弹簧振子作简谐振动，总能量为E1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E2变为（A）E1/4．（B）E1/2．（C）2E1．（D）4E1．4（3562）　图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，则合成的余弦振动的初相为（A）．（B）．（C）．（D）0．5（3066）　机械波的表达式为y=0.03cos6p（t+0.01x）（SI），则（A）其振幅为3m．（B）其周期为．（C）其波速为10m/s．（D）波沿x轴正向传播．11\n6（5204）　一平面余弦波在t=0时刻的波形曲线如图所示，则O点的振动初相f为：（A）0．（B）．（C）p．（D）（或）．7（3382）　在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振动的周期之比为_______________________．8（3819）　两质点沿水平x轴线作相同频率和相同振幅的简谐振动，平衡位置都在坐标原点．它们总是沿相反方向经过同一个点，其位移x的绝对值为振幅的一半，则它们之间的相位差为______________．9（3033）　一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A=_________；w=_________；f=_________．10（5314）　一质点同时参与了两个同方向的简谐振动，它们的振动方程分别为（SI）,（SI）其合成运动的运动方程为x=__________________________．11（3135）　如图所示为一平面简谐波在t=2s时刻的波形图，该简谐波的表达式是__________________________________；P处质点的振动方程是____________________________．（该波的振幅A、波速u与波长l为已知量）12（3344）　一简谐波沿Ox轴负方向传播，x轴上P1点处的振动方程为(SI)，x轴上P2点的坐标减去P1点的坐标等于（为波长），则P2点的振动方程为__________________________________________．13（5517）　S1，S2为振动频率、振动方向均相同的两个点波源，振动方向垂直纸面，两者相距（l为波长）如图．已知S1的初相为．(1)若使射线S2C上各点由两列波引起的振动均干涉相消，则S2的初相应为________________________．(2)若使S1S2连线的中垂线MN11\n上各点由两列波引起的振动均干涉相消，则S2的初位相应为_______________________．14（5506）　一物体质量m=2kg，受到的作用力为F=-8x（SI）．若该物体偏离坐标原点O的最大位移为A=0.10m，则物体动能的最大值为多少？15（5189）　一物体同时参与两个同方向的简谐振动：（SI）,（SI）求此物体的振动方程．16（3265）　在一轻弹簧下端悬挂m0=100g砝码时，弹簧伸长8cm．现在这根弹簧下端悬挂m=250g的物体，构成弹簧振子．将物体从平衡位置向下拉动4cm，并给以向上的21cm/s的初速度（令这时t=0）．选x轴向下,求振动方程的数值式．17（3384）　一台摆钟每天快1分27秒，其等效摆长l=0.995m，摆锤可上、下移动以调节其周期．假如将此摆当作质量集中在摆锤中心的一个单摆来考虑，则应将摆锤向下移动多少距离，才能使钟走得准确？18（3825）　有一单摆，摆长为l=100cm，开始观察时（t=0），摆球正好过x0=-6cm处，并以v0=20cm/s的速度沿x轴正向运动，若单摆运动近似看成简谐振动．试求（1）振动频率；（2）振幅和初相．19（3335）　一简谐波，振动周期s，波长l=10m，振幅A=0.1m．当t=0时，波源振动的位移恰好为正方向的最大值．若坐标原点和波源重合，且波沿Ox轴正方向传播，求：（1）此波的表达式；（2）t1=T/4时刻，x1=l/4处质点的位移；（3）t2=T/2时刻，x1=l/4处质点的振动速度．20（3860）　一振幅为10cm，波长为200cm的简谐横波,沿着一条很长的水平的绷紧弦从左向右行进，波速为100cm/s．取弦上一点为坐标原点，x轴指向右方，在t=0时原点处质点从平衡位置开始向位移负方向运动．求以SI单位表示的波动表达式（用余弦函数）及弦上任一点的最大振动速度．21（3138）　某质点作简谐振动，周期为2s，振幅为0.06m，t=0时刻，质点恰好处在负向最大位移处，求（1）该质点的振动方程；（2）此振动以波速u=2m/s沿x轴正方向传播时，形成的一维简谐波的波动表达式，（以该质点的平衡位置为坐标原点）；（3）该波的波长．11\n22（3140）　如图所示，一平面简谐波沿Ox轴正向传播，波速大小为u，若P处质点的振动方程为，求（1）O处质点的振动方程；（2）该波的波动表达式；（3）与P处质点振动状态相同的那些质点的位置．11