大学物理 电介质 14页

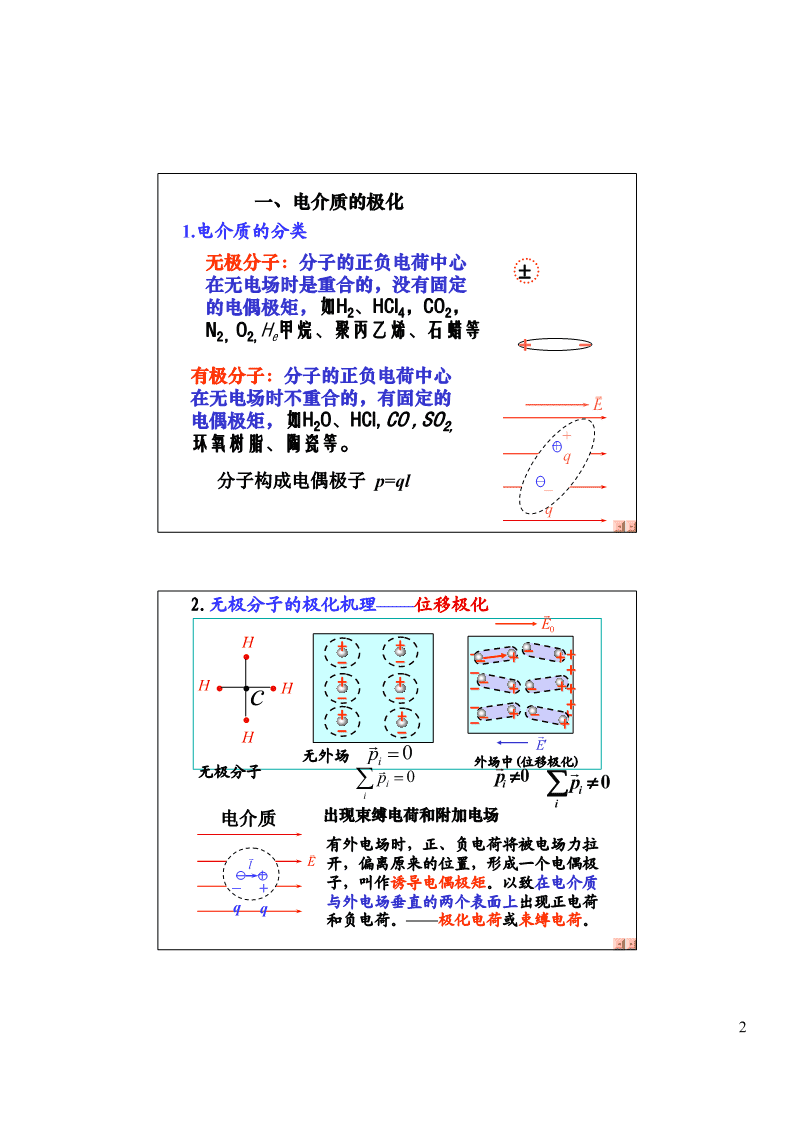
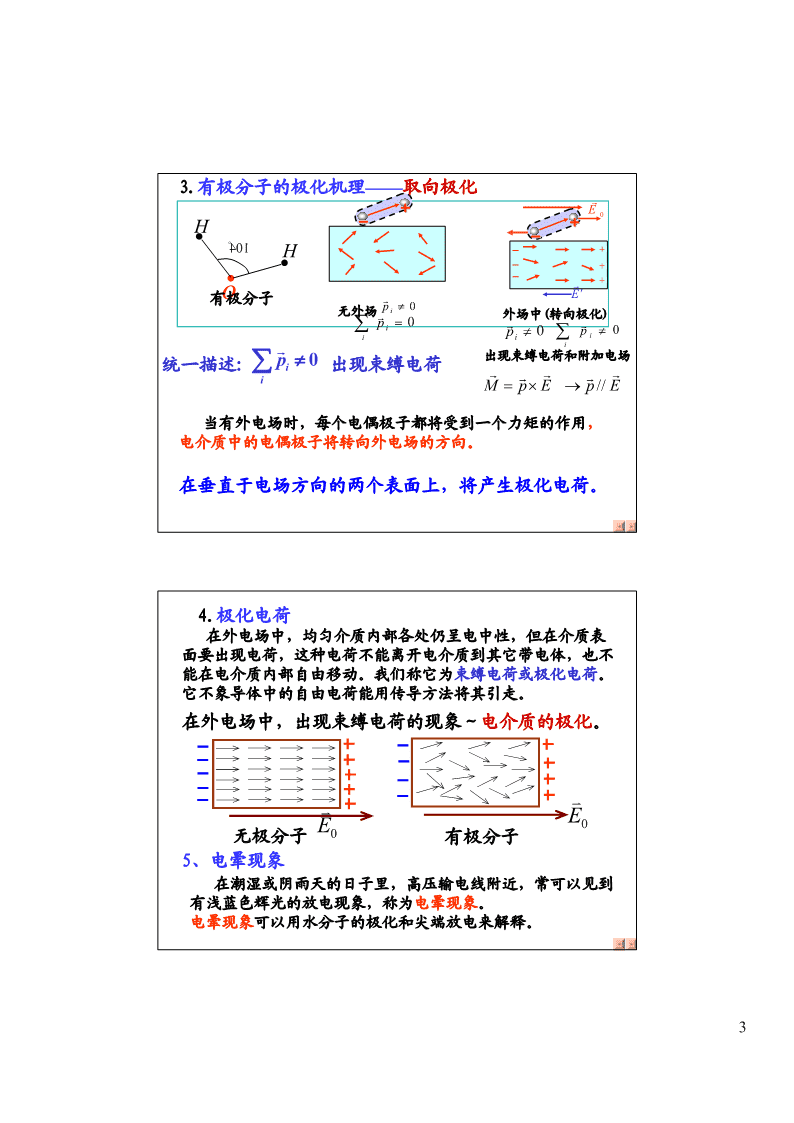
静电场中的电介质（DielectricInElectrostaticField）带静电的梳子吸引水柱§3-1静电场中的电介质所谓电介质，就是通常所说的由大量电中性的分子组成的绝缘体。在静电场中平衡时：1.内部电场强度不为零；2.电介质表面出现极化电荷。电介质出现极化电荷的现象，称为电介质极化。若把电介质放入静电场中，电介质原子中的电子和原子核在电场力的作用下，在原子范围内作微观的相对位移。在外电场中电介质要受到电场的影响，同时也影响外电场。1\n一、电介质的极化1.电介质的分类无极分子：分子的正负电荷中心±在无电场时是重合的，没有固定的电偶极矩，如H2、HCl4，CO2，N2，O2,He甲烷、聚丙乙烯、石蜡等+-有极分子：分子的正负电荷中心在无电场时不重合的，有固定的KE电偶极矩，如H2O、HCl,CO,SO2,+环氧树脂、陶瓷等。+q分子构成电偶极子p=ql––q2.无极分子的极化机理——位移极化GE0H++-•----+++-+H•••cH++--+-++---++•++--+-+H-G-GE′无外场pi=0外场中(位移极化)G无极分子Gp≠0G∑pi=0i∑p≠0iii电介质出现束缚电荷和附加电场有外电场时，正、负电荷将被电场力拉KKlE开，偏离原来的位置，形成一个电偶极–+–+子，叫作诱导电偶极矩。以致在电介质qq与外电场垂直的两个表面上出现正电荷和负电荷。——极化电荷或束缚电荷。2\n3.有极分子的极化机理——取向极化G+E0H-+•-°104H+•+•G+有极分子oGE′p≠0无外场Gi外场中(转向极化)∑pi=0GGipi≠0∑pi≠0Gi统一描述:∑p≠0出现束缚电荷和附加电场i出现束缚电荷GGGGGiM=×→pEpE//当有外电场时，每个电偶极子都将受到一个力矩的作用，电介质中的电偶极子将转向外电场的方向。在垂直于电场方向的两个表面上，将产生极化电荷。4.极化电荷在外电场中，均匀介质内部各处仍呈电中性，但在介质表面要出现电荷，这种电荷不能离开电介质到其它带电体，也不能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。它不象导体中的自由电荷能用传导方法将其引走。在外电场中，出现束缚电荷的现象～电介质的极化。KKEE0无极分子0有极分子5、电晕现象在潮湿或阴雨天的日子里，高压输电线附近，常可以见到有浅蓝色辉光的放电现象，称为电晕现象。电晕现象可以用水分子的极化和尖端放电来解释。3\n金属导体和电介质比较金属导体电介质（绝缘体）有大量的基本无自由电子，正负电荷特征自由电子只能在分子范围内相对运动模型“电子气”电偶极子与电场的无极分子电介质:位移极化静电感应相互作用有极分子电介质:转向极化静电平衡G内部：分子偶极矩矢量宏观导体内E=0,ρ=0和不为零∑pG≠0Gi效果导体表面iE⊥表面表面：出现束缚电荷感应电荷σ=ε0E（极化电荷）二、电极化强度(polarization)在宏观上测量到的是大量分子电偶极矩的统计平均值，为了描述电介质在外场中的行为引入一个物理量：1.电极化强度矢量:单位体积内分子的电偶极矩的矢量和。KK∑pP=ΔSKΔVGG+++++++++++p：分子电偶极矩pqii=ri−σ'-----KKP：电极化强度εPrlσ'：极化电荷面密度+σ'+++++-----------∑pσ'ΔSlP===σ'ΔΔVSl4\n三、极化电荷对场强的影响处于静电场E0中的电介质由于极化而在其表面上产生极化电荷，极化电荷在空间产生的电场称为附加电场，用E′表示。KKK空间各处的电场强度EE=E+E'0在电介质内部，由于E′与E的方向相反，于是0有E=E−E′，在电介质内部的附加电场E′有一0个特殊的名称，叫做退极化场(depolarizationfield)。电介质对电场的影响相对电容率以平行板电容器为例,如果极板电容器上所带自由电荷面密度分别为+σ和−σ，实验表明：++++++++σ++++++++σεr-------−σ-------−σσE0E=E=0εε0rεr相对电容率是一个大于1的常数，其大小随电介质的种类和状态的不同而不同χ=−ε1电极化率r令εχ=+(1)为相对介电常量（相对电容率）reε=εε0r～电介质的电容率5\n四、极化电荷与自由电荷的关系E0+++++++++++E=E−E'=0-----εrKKKεr−1dεrE0E'EE'=E0εr+++++-----------εr−1Q'=εr−1Qσ'=σ00εεrrKKE=σ/ε实验表明：P=（ε−1)εE000r0E=E/εχ=−ε1电极化率0rKrKP=χεEP=σ'0只限于讨论各向同性的均匀的电介质。+Q–Q+Q–Q一、电介质对电容的影响研究：结构、形状一定的电容器，其电容C与极板间均匀的各向同性电介质之间的关系。•插入电介质前后，极板带电量Q不变，两极板间的电压分别用U、U表示，01静电计测电压实验表明：U=U0εr6\n充满电介质电容器的电容为QQC==0=εCr0UU/ε0r1E=E0εr真空中E=U/d00电介质中E==UdU//(0εr)/d==()Ud//εE/ε00rr五、电介质存在时的高斯定理KK11.根据真空中的高斯定理∫∫E⋅dS=∑qiSε0i而现在电场中有电介质，高斯面内可能同时包含自由电荷和极化电荷这两种电荷，高斯定理应表示为：KK1束缚电荷'E⋅dS=(Q−Q)∫0Sε0自由电荷S'εr−1+++++++++++QQ=0−σ'-----εrKKQε0r∫E⋅dS=Sεε0r+σ'+++++KK-----------εεE⋅dS=Q∫S0r0KK电容率εεε=0r∫SεE⋅dS=Q07\nKKεE⋅dS=Q∫0S定义电位移矢量KelectricdisplacementKKD=εεE=εE0rKK电位移通量∫D⋅dSS有介质时的高斯定理KKn∫D⋅dS=∑Q0iSi=1有介质时的高斯定理GGD⋅dS=q自由电荷∫∑0s物理意义s内对于任一闭合曲面电感应强度的通量，等于该闭合曲面内所包围的自由电荷的代数和。KKGD＝εεE=εE0r•电位移线起始于正自由电荷终止于负自由电荷，与束缚电荷无关。•电力线起始于正电荷终止于负电荷，包括自由电荷和束缚电荷。8\nKKK2、PDE、、之间的关系：KKKKKD=+=+εEPEεχεE000KKDE=+()1χε0εr=+(1χ)ε=εεr0相对电容率或相对介电常量电容率或介电常量KKGD＝εεE=εE0r•注意：KKD是辅助矢量，描写电场性质的物理量仍为KEK,V对于真空χe=0εr=1ε=ε0则D=ε0E3、有电介质时的高斯定理的应用利用电介质的高斯定理可以使计算简化，原因是只需要考虑自由电荷，这样可以避免求极化电荷引起的麻烦。1)由高斯定理求出电位移矢量D的分布，2)再由电位移矢量D的分布求出电场强度E的分布，KKKGD=εεED⋅dS=qK0rG∫S∑0P=ε(ε−1)E0r有电介质存在时解题均应先求D再求E等！！GGG即DEP⇒⇒⇒σ′⇒q′9\n物理意义特点G单位试验电荷真空中关于电场的讨论都E的受力适用于电介质：高斯定律、电势的定义、环路定理等G单位体积内的各向同性均匀电介质中GGP电偶极矩的矢P=εχE，表面束缚电荷0GeGG量和σ′=P⋅n，电介质中P≠0GG无物理意义，穿过任意闭合曲面的D的D只有一个数学通量只与面内自由电荷有关上的定义GGGGGDEP=+εD⋅=dSq0v∫S自由G=εεE0r例1:如图金属球半径为R1、带电量+Q；均匀、各向同GG性介质层外半径R2、相对介电常数εr,求：D、E、U分布GG解:由对称性分析确定E、D沿矢径方向以球心为中心、以大于R的任意长r为半RKK1R径作球形高斯面，2D⋅dS=q∫∑0CBAQSKKGεr由高斯定理可求得D＝εεE=εE0r大小DA=0EA=0QQrDB=2DB=εEEB=4πr4πεεr200rQQDC=4πr2DEC=ε0EC=24πεr010\n∞GGU=E⋅drA∫rR1GGR2GG∞GG=E⋅dr+E⋅dr+E⋅dr∫A∫∫BCrRR12Q⎛111⎞R=⎜−+⎟1R⎜⎟24πεεRεRR0⎝r1r22⎠CBAQR2GG∞GGεU=E⋅dr+E⋅drrB∫rB∫RC2Q⎛111⎞=⎜−+⎟⎜⎟4πεεrεRR0⎝rr22⎠∞GGQU=E⋅dr=C∫Cr4πεr0+σ–σ例2：平行板电容器充满两层厚度为d和d的电介质(d=d+d)，1212S相对电容率分别为ε和ε。1S2r1r2求：1.电介质中的电场；2.电容量。解：设两介质中的电感应强度为D1和D，由高斯定理知：2KKd1d2D⋅dS=D⋅A=σA∫∫111S1介质中的场强：Dσ10∵D=σ∴E==111εεε0r11σD=σE=0同理得到222ε211\n板间电势差：KK⎛dd⎞⎜12⎟U=E⋅dl=Ed+Ed=+σAB∫1122⎜⎟εεAB⎝12⎠+σ–σ电容器的电容：QSSSC==21UABd1d2(+)εε12dd12以上两个例题的求解，都是绕过了极化电荷的影响，通过电感应强度矢量D进行的，使问题大为简化了。解二：看为串联+σ111+++++++++++0=+CCCd121‐‐‐‐‐‐‐‐‐‐−σ0S++++++++++σ0C=εεd10r12d1‐‐‐‐‐‐‐‐‐‐‐S−σC=εε020r2d2QSεεε00r1r2C==Uddεε+r12r2112\n例3:在盖革计数器中有一直径为2.00cm的金属圆筒，在圆筒轴线上有一条直径为0.134mm的导线。如果在导线与圆筒之间加上850V的电压，试分别求：（1）导线表面处（2）金属圆筒内表面处电场强度大小解：设导线上的电荷线密度为λ，与导线同轴作单位长度的、半径为r的（导线半径R1