大学物理磁介质 43页

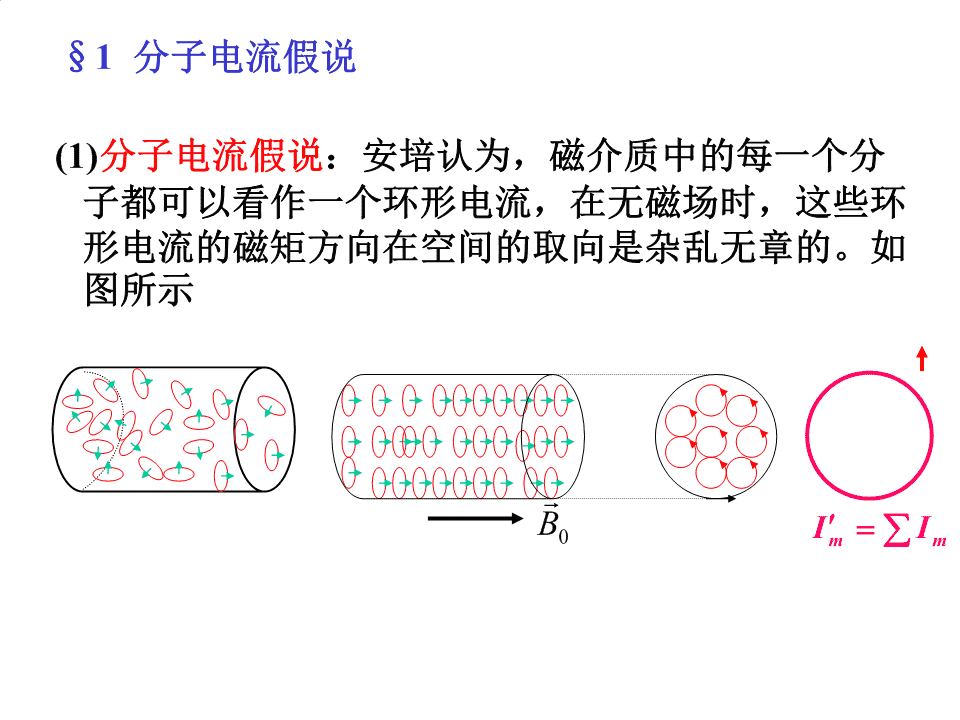
第5章磁介质（magneticmedium）1\n目录§5.1“分子电流”模型§5.2顺磁质与抗磁质§5.3磁介质的磁化规律§5.4有磁介质存在时的磁场H的环路定理§5.6铁磁介质§5.7磁场的边界条件2\n§1分子电流假说(1)分子电流假说：安培认为，磁介质中的每一个分子都可以看作一个环形电流，在无磁场时，这些环形电流的磁矩方向在空间的取向是杂乱无章的。如图所示B0ImIm\n1、电子的轨道磁矩zeeveiplT2r2-e,me轨道磁矩2PiSnˆervm,电子2ev轨道角动量r2PiS(r)m,电子L2revreeLpL22ml2mL:轨道角动量eeUsefulindiscussingtheatomicangularmomentumbecauseitisquantized\n2、电子自旋磁矩相对论效应ep2SS:自旋角动量s2me3、磁矩的量子化角动量是量子化的，其取值只能是普朗克常数34的整数或半奇数倍。1.0510Js磁矩(轨道、自旋磁矩)和角动量成正比，因此，磁矩也是量子化的。\n3、磁矩的量子化角动量是量子化的，其取值只能是普朗克常数34的整数或半奇数倍。1.0510Js磁矩(轨道、自旋磁矩)和角动量成正比，因此，磁矩也是量子化的。电子磁矩的取值，等于玻尔磁子me9.271024J/TB2me的整数倍。6\n4、原子核的磁矩等于核磁子的整数倍ee核磁子玻尔磁子2mp2me原子核的磁矩可以忽略。5、分子的固有磁矩所有电子的轨道磁矩和自旋磁矩的矢量和经典电磁学：用圆电流等效S固有磁矩I－“分子电流模型”pIS7\n§2顺磁质(paramagetic)与抗磁质(diamagnetic)B＝Br0—相对磁导率r顺磁质抗磁质铁磁质8\n顺磁质（例如铝）11.651051r工程上取r1抗磁质（例如铜）r11.01051铁磁质（铁、钴、镍及其合金，铁氧体）r1且与B0有关纯铁硅钢坡莫合金r510371021105介质的磁性9\n1、顺磁介质B0ImIm分子具有固有磁矩固有磁矩趋向外磁场方向B0pmMjMpBmBB0表面出现束缚(磁化)电流加强磁场\n2、抗磁介质分子固有磁矩(电子轨道、自旋磁矩的矢量和）为零。但是，电子磁矩在外磁场力矩作用下进动产生和外磁场反向的感生磁矩。jBB0出现反向的表面束缚电流减弱磁场11\n3、抗磁质的磁化抗磁质分子的固有磁矩为零（分子中各电子有磁矩，但磁效应相互抵消）加磁场时，看一个电子的磁距：.ΔLdL.MpmBeMdt若从上往下看，电子轨道作L顺时针方向进动。pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np在外磁场作用下Δm电子轨道的进动L电子轨道平面pmB0\np3、抗磁质的磁化Δm抗磁质分子的固有磁矩为零（分子中各电子有磁矩，但.磁效应相互抵消）ΔL加磁场时，看一个电子的磁距：.dLeM电MpmB子dtL轨若从上往下看，电子轨道作p道顺时针方向进动。m进由此产生等效的，逆时针方向动的分子电流。方向分子电流产生的附加磁矩和外磁场B0方向相反\n分子电流所产生的附加磁矩方向和外磁场方向相反，附加磁矩产生的附加磁场和外磁场相反。所以抗磁质磁化结果使介质内部的磁场削弱。即：BB0\n§3磁化的规律1、磁化强度（1）定义pmMV其中：pm对于顺磁质是指分子磁矩；对于抗磁质是指分子附加磁矩。对于顺磁质和抗磁质（统称弱磁质），介质中某一点磁化强度和该处的磁感应强度成正比：m——磁化率mr1m1MBMrB——介质磁导率0r0r\n(2)顺磁质的磁化当顺磁质中存在磁场时，分子电流的磁矩将与磁场方向趋于一致。这就是磁介质的磁化。出现束缚磁化电流ImIm(3)为了描述分子磁矩在磁场中的取向排列的整齐程度，定义磁化强度矢量：pmPM比较:PeVV(4)磁介质内部的磁感应强度由于磁介质被磁化，磁化电流将在磁介质中激发磁场，因此，磁介质中任一点P的磁感应强度应该为:BBB0\n式中为P点的合磁感应强度，B0为外磁场在P点的B磁感应强度，B为磁化电流在P点产生的磁感应强度。2、磁化电流与磁化强度关系假设：①介质宏观体积内，每个分子电流Im都相同；②每个分子电流所围面积为S0；③分子磁距pm取向相同。pmNpmMnpnISmm0VV由特例给出(均匀磁化的柱形棒)B0ImIm\n由特例给出(均匀磁化的柱形棒)(1).M与磁化面电流密度j'的关系:MVMLSMadbpmc又I'Sj'LS故j'M写成矢量形式:j'Mnˆ此式具有普遍意义(2).M与I的关系取图示的回路,则有:bcdaMdlaMdlMdlMdlMdlMLIbcdL故有:IMdlI’为S面上的电流,L为S面的边界L\n•我们现在推导磁化电流与磁化强度矢量的关系：如图LdlSBCAdl(a)(b)n在介质中任取一以L为边界的曲面S，计算通过曲面S的磁化电流I，分子电流与S的关系可分为三种情况:（A）与S不相交；(B)被S切割，与S相交二次；(C)被S的边界L穿过，与S相交一次。\nLdlSBCAdl(b)n(a)前二种(A)(B)对I无贡献,只有(C)对I有贡献。在边界线L上任取一线元dl以dl为轴线，以S0为底面，作斜圆柱体，其体积为：dVSdl0凡中心在圆柱体内的分子电流都被dl穿过，数量为nS0dl，贡献为dIImnS0dlMdl所以IMdl对比qPdSLs\n•磁化电流面密度与磁化强度关系:•若将dl取在介质表面处，且垂直于磁化电流线，定义单位长度上的磁化面电流为磁化电流面密度：dIMdljMcosMtdldl当M与表面平行时(0,cos1)jM,jM.nˆnˆMjMnˆIdljdlM\n§3磁场强度H,磁介质中的安培环路定理和高斯定理1.磁场强度H有磁介质时，III(I是传导电流，I是磁化电流。）00Bdl0I0(I0I)0(I0Mdl)BLLHMB0即(M)dlI0.令H为磁场强度：L03H的单位是：A/m410Oe(奥斯特）则磁介质中的安培环路定理为:HdlI0B真空时M0,H.L0B得HdldlI0.即Bdl0I0.LL0L\n•由于磁化电流与传导电流在产生磁场方面性质相同，故有介质时,高斯定理仍成立(普适性)：BdS0S•说明:磁场是无源场,是涡旋场.\n2、磁化率和磁导率,B,H,M的关系对大多数磁介质，实验证实,磁化强度与磁场强度成正比，即MHm─磁介质的磁化率。是一个纯数m定义磁介质相对磁导率为1rm磁介质的绝对磁导率(磁导率)为0rBB于是在磁介质中有：HMHm00B(1)HHH0m0rBH对比DE\n[例题]一圆柱形电流电流强度为I，置于的无限大磁导率为的磁介质中r，求柱外任一点的B,H解∶取圆形回路为安培回路，则有IIHdlI2rHIHr2rLIr0rRBH(rR)0r2r在充满均匀磁介质场中磁感应强度为真空中的r倍.\n例：一根长直单芯电缆的芯是一根半径为R的金属导体，它和导电外壁之间充满相对磁导率为r的均匀介质。今有电流I均匀地流过芯的横截面并沿外壁流回。求磁介质中磁感应强度的分布。解：由安培环路定理HdlIi内riHdlHdlH2rIIIH0rBH0r2r2r\n求轴导线间单位长度截面上的磁通量I0rdBdSBdSldrm2rR20rImldrBR12rrIlRll0r2lndr2R1IRm0r2lnl2R1\n§5.6铁磁质铁磁质铁、钴、镍及某些合金等物质测量磁滞回线的实验装置电流表测量B的探头A（霍尔元件）测量H换51015向020铁环开狭缝关磁强计电阻螺绕环\n从磁强计中可以测得BA51015根据电流的测量再由式020NI磁强计H2R磁滞回线计算得到HBH矫顽力cc——.B.B——剩余磁感应强度rbr.aBsBs——饱和磁感应强度.ee..初始磁化曲线HoHHcc磁滞现象：B滞后于H的变化g.Brf.\n铁磁质的特性：1.磁导率不是一个常量，它的值不仅决定于原线圈中的电流，还决定于铁磁质样品磁化的历史。B和H不是线性关系。B，r2.有很大的磁导率。放入线圈中时可以使磁场增强102~104倍。B~H3.有剩磁、磁饱和及磁滞现象（磁滞损耗）。4.有居里温度——T≥Tc时，r~H铁磁质变为顺磁质H铁磁质的量子解释：磁畴Fe：1040K，Co：1388K，Ni：631K\n铁磁质的磁化机理——磁畴在铁磁质中，相邻原子的核外电子之间存在非常强烈的“交换耦合”作用，使得这些电子的自旋磁矩按同方向排列起来（自发磁化），形成饱和磁化状态的微小区域，称为“磁畴”。\n1、磁畴的基本特点：磁畴的体积≈10-8—10-10m3同一磁畴内的电子磁矩方向均相同无外磁场时，不同磁畴的电子磁矩的取向杂乱无章2、铁磁质的磁化机理有外磁场时，各个磁畴的取向随磁场增强而趋于与外磁场同向，当所有磁畴变为与磁场同向时，即达到饱和磁化状态。Bo\nBo当再撤去外磁场时，各个磁畴间的摩擦阻力阻碍它们恢复到磁化以前的取向分布，从而表现出过程的不可逆性，即：磁滞效应。在高温下，强烈的热运动会瓦解磁畴内电子磁矩的规则排列，当达到一定程度时（居里温度），磁畴全部被破坏。铁磁质的应用\n磁性材料：软磁材料特点：磁导率大，矫顽力小，磁滞回线窄应用：硅钢片，作变压器的铁芯。铁氧体（非金属）作高频线圈的磁芯材料。硬磁材料特点：剩余磁感应强度大，矫顽力大，磁滞回线宽。应用：作永久磁铁，永磁喇叭矩磁材料：作计算机中的记忆元件。\n铁磁质BBH1r0顺磁质抗磁质oH起始磁化曲线\n复习：三种磁介质:顺磁质（paramagetic）、抗磁质（diamagnetic）、铁磁质（ferromagnetic）pm磁场强度矢量MV磁化电流与磁化强度关系IMdlL磁场强度H,磁介质中的安培环路定理和高斯定理有磁介质时，III(I是传导电流，I是磁化电流。）00BdlI(II)(IMdl)00000LLB即(M)dlI.令H为磁场强度：0L0\n磁化率和磁导率,B,H,M的关系BBHMHB(1)HHHm0m0r00BHBBHOOH(a)硬磁性材料的(b)软磁性材料的磁回线磁回线