《大学物理》PPT课件 39页

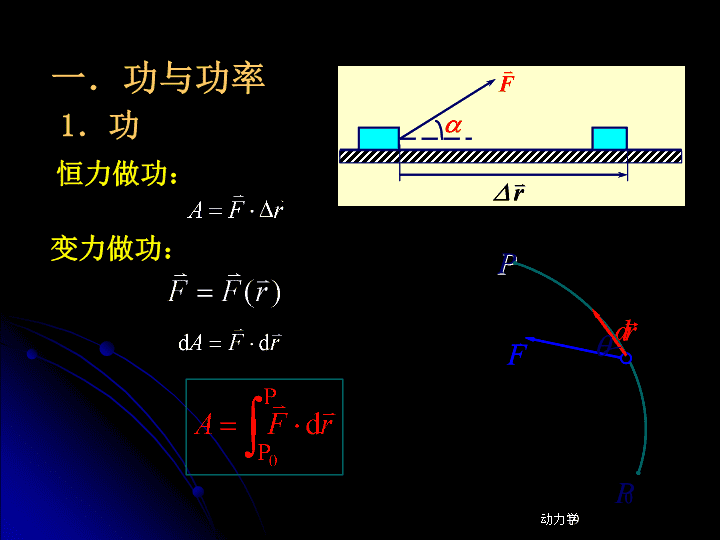
第二章质点动力学\n§2.4功动能定理\n1．功一．功与功率变力做功：恒力做功：PP动力学19rdrFv0PqPPrdrFv0Pq\n直角坐标系：自然坐标系：一维运动：动力学1919PPFv0PnFvtFv19PPFv0PPPFv0PPPFv0PnFvtFvnFvtFvnFvtFv\n2.功率直角坐标系：自然坐标系：一维运动：\n功和功率都是标量，无方向，但有正负号。合力的功和功率：功和功率的关系：\n一质量为2kg的物体在变力作用由静止沿x轴运动，试求：<1>前2s内变力的功，<2>第1s末和第2s末的功率例2-8解：\n二．动能动能定理质点的动能：动能定理：\n三．质点系的动能定理内力所做的总功一般不为零，即内力一般要改变系统的总动能功是过程函数，动能是状态函数；功是动能变化的手段和量度。\nO\n例：mMm+M\n例2-5A球的质量为，以速度运动，与一静止的小球B碰撞后，A球的速度变为，其方向与方向成90°角，B球的质量为，它被碰撞后以速度运动，的方向与成角。试求：两小球相撞后速度，的大小；AAB碰撞后两小球动能的变化？\n例2-9如图，一长度为l，密度为r的细棒从下端紧贴水面的位置，以零初速落入密度为)(00rrr<，深度为h)(lh>的水池中。求细棒下端接触到水池底时的速度。hlx\n\n§2.5势能功能原理机械能守恒定律\n一.质点系的势能1．保守力重力做功：\n弹力作功：\n万有引力做功：\n或保守力：作功只与质点的前、后位置有关，而与运动路径无关的力；或质点沿任一闭合路径运动一周，做功都为零的力:\n2．势能保Fr若保守力做功可表为0rdFPPvvv-=ò保)]()([0rrF[F-则)(rEprF=称为质点在rv处的势能。v\n重力势能:弹力势能:万有引力势能:\n势能只对保守力引入，势能属于系统。势能是相对位置函数，具有相对意义，与零点选取有关。势能差具有绝对意义。势能曲线：Ep=mgyOEpyEpOxOEpr\n1.质点系动能定理（n个质点组成的系统）二．功能原理\n动能定理作用于质点系的所有力所做的功，等于该质点系的动能的增量。\n机械能:功能原理:所有外力与非保守内力所做功的代数和，等于质点系的机械能的增量。2.功能原理\n三.机械能守恒定律\n四．能量的转化与守恒定律自然界中，能量既不能消失，也不能创造，它只能从一种形式转化成另一种形式，或者从一个物体传给另一个物体。自然界中有许多形式的能量。封闭系统:能量守恒，但机械能不一定守恒；封闭保守系统:能量守恒，机械能守恒。\n水力发电风力发电太阳能力发电无轨电车太阳能热水器拖拉机几种能量转化的实例\n质点动力学知识链:牛顿第二定律1引入动量定理动量守恒定律2引入A,Ek动能定理引入EP功能原理引入E机械能守恒定律\n质点动力学问题解题思路沿着知识链1、2逆向进行，在不涉及打击、碰撞等问题时，可以断掉链1，选择机械能守恒定律和牛顿第二定律解题，或选择动能定理（功能原理）和牛顿第二定理解题。\n方法一aomgfrNb例2-10质量2kg物体，沿半径为4m的四分之一圆弧从a点由静止滑到b点，，求：从a到b点过程中摩擦力所做的功。\n质量2kg物体，沿半径为4m的四分之一圆弧从a点由静止滑到b点，，求：从a到b点过程中摩擦力所做的功。例2-10\n方法二应用动能定理质量2kg物体，沿半径为4m的四分之一圆弧从a点由静止滑到b点，，求：从a到b点过程中摩擦力所做的功。例2-10mgfrNb\n方法三应用功能原理质量2kg物体，沿半径为4m的四分之一圆弧从a点由静止滑到b点，，求：从a到b点过程中摩擦力所做的功。例2-10将质点和地球视为一个力学系统，有：mgfrNb\n长为L，质量为m的匀质链条，置于桌面上，链条与桌面的摩擦系数为，下垂端的长度为a。在重力作用下，由静止开始下落，求链条完全滑离桌面时，重力，摩擦力的功,链条末端离开桌面时的速度。解：设链条下落y长度时，重力为摩擦力为例2-11\n长为L，质量为m的匀质链条，置于桌面上，链条与桌面的摩擦系数为，下垂端的长度为a。在重力作用下，由静止开始下落，求链条完全滑离桌面时，重力，摩擦力的功，链条末端离开桌面时的速度。解：重力的功：摩擦力的功：例2-11\n长为L，质量为m的匀质链条，置于桌面上，链条与桌面的摩擦系数为，下垂端的长度为a。在重力作用下，由静止开始下落，求链条完全滑离桌面时，重力，摩擦力的功，链条末端离开桌面时的速度。解：例2-11利用功能原理：取桌面为零势能面\n例2-12质量分别为m1和m2的两小球A、B经屈强系数为k的弹簧相连，静止地放在光滑的水平面上，一质量与A球相等的小球C以速度v0与小球A发生完全弹性碰撞。求：(1)碰撞后A球的速度；(2)弹簧被压缩的最大长度；\n(1)由于mC=mA，所以球C和球A发生弹性碰撞后，两者交换速度，即碰撞后球A的速度为v0。(2)小球A、B速度相等(设等于v)时，弹簧被最大压缩(设最大压缩长度为xm)。动量守恒和机械能守恒: