大学物理力学PPt 49页

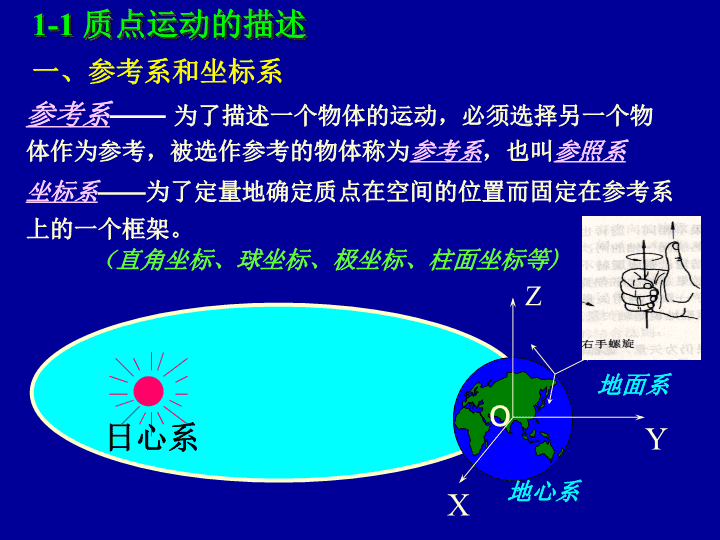
质点运动学第一章第一篇力学宏观物体之间（或物体各部分间）在空间的位置随时间变化的运动称为机械运动。\n日心系地心系ZXYo1-1质点运动的描述参考系——为了描述一个物体的运动，必须选择另一个物体作为参考，被选作参考的物体称为参考系，也叫参照系地面系一、参考系和坐标系坐标系——为了定量地确定质点在空间的位置而固定在参考系上的一个框架。（直角坐标、球坐标、极坐标、柱面坐标等)\n注意参考系不一定是静止的。对于同一种运动，由于参考系选择的不同而有不同的描写。运动描述的相对性参考系与坐标系的区别参考系选定后，选用不同的坐标系对运动的描写是相同的。但运动方程的具体形式不同。对物体运动的描写决定于参考系而不是坐标系。\n二、物理模型质点没有大小和形状，只具有全部质量的一点。可以将物体简化为质点的两种情况：物体不变形，不作转动(此时物体上各点的速度及加速度都相同，物体上任一点可以代表所有点的运动)。物体本身线度和它活动范围相比小得很多(此时物体的变形及转动显得并不重要)。刚体在讨论问题时可以忽略由于受力而引起的形状和体积的改变的理想模型可以将物体简化为刚体的两种情况：物体不变形。物体各部分间相对活动范围很小(此时物体的变形显得并不重要)。当物体的转动不能忽略时，质点模型无意义\n(一)、位置矢量质点的空间位置可以用它在坐标系中的坐标来表示。P点坐标(x,y,z)P点矢径位置矢量(位矢、矢径)P点矢径方向P点矢径大小单位：米ββrPxyzO轨道三、描述质点运动的四个物理量强调质点的位矢既具有大小又具有方向。位矢是矢量\n（二）、运动方程(运动函数)位矢位矢随时间的某种函数关系质点的运动学方程直角坐标系中分量表示可以简化为一维、二维和三维运动方程。运动轨道：运动质点所经空间各点联成的曲线。轨道方程：表示轨道曲线的方程式。消去t，得到轨道方程f(x,y,z)=0例：圆\n(三)、位移r2r1ΔrxyzBAoΔS··时间内位置变化有向线段单位：米t时间内的位移\n注意r2r1ΔrxyzBAoΔS··位移是矢量，有大小和方向r与的区别s与的区别s为路程(轨道长度)，是标量元位移的大小元路程r2r1oΔrΔra)为标量，为矢量b)\n(四)、速度1.平均速度r2r1ΔrBAoΔS··t时间内，完成同样的位移质点位置变化的快慢平均速度矢量大小方向与同向平均速度的大小和方向与所取时间间隔有关，表述时必须指明是哪一段时间间隔内的平均速度。单位：米/秒\n2.瞬时速度(简称速度)速度等于位置矢量对时间的一阶导数速度方向时，的极限方向在A点的切线并指向质点运动方向直角坐标系中速度大小\n质点运动路程s与时间t的比值称为t时间内的平均速率质点运动的路程对时间的一阶导数(瞬时)速率注意速度是矢量，速率是标量。一般情况单向直线运动情况3.平均速率和瞬时速率单位：米/秒平均速率瞬时速率等于瞬时速度的大小\n(五)、加速度单位：米/秒2描述速度变化的快慢(包括大小和方向的变化)Δvv1v2yxzBAov1v2··t时间内的平均加速度t时间内速度的增量t时刻的瞬时加速度(简称加速度)质点在某时刻的加速度等于该时刻质点速度矢量对时间的一阶导数，或位置矢量对时间的二阶导数。\n直角坐标系中加速度大小注意矢量性：四个量都是矢量，有大小和方向加减运算遵循平行四边形法则某一时刻的瞬时量不同时刻不同过程量瞬时性：加速度位矢位移速度相对性：不同参考系中，同一质点运动描述不同不同坐标系中，具体表达形式不同\n叠加性：任一曲线运动都可以分解成沿x,y,z三个各自独立的直线运动的叠加运动的独立性原理(运动的叠加原理)描述质点运动状态的物理量描述质点运动状态变化的物理量\n特别指出讨论问题一定要选取坐标系注意矢量的书写与的物理含义运动学问题类型：已知运动方程，求质点的速度和加速度已知质点的速度(或加速度)和初始条件，求质点运动方程及其它未知量求导数运用积分方法\n匀加速运动为常矢量初始条件给定，质点运动确定地面忽略空气阻力，质点运动由初始条件可预知匀加速直线运动为常矢量，和在一条直线上*实际有些自由落体受空气阻力很大，如雨点最终匀速运动，此时速率称收尾速率（~10m/s）只用一维描述如自由落体1-2加速度为恒矢量时的质点运动\n抛体运动典型的匀加速运动，运动叠加和运动的独立性运动平面在内yxv00实际子弹和炮弹受空气阻力很大，弹道导弹则在重力加速度变化的范围运动，但基础是以上的运动学。\n例题1.一质点由静止开始作直线运动，初始加速度为a0，以后加速度均匀增加，每经过τ秒增加a0，求经过t秒后质点的速度和运动的距离。(直线运动中可用标量代替矢量）解：据题意知，加速度和时间的关系为：\n实际上可以用求面积的方法。解：2.一质点沿x轴作直线运动，其v-t曲线如图所示，如t=0时，质点位于坐标原点，求：t=4.5秒时，质点在x轴上的位置。v(m/s)t(s)-121012342.54.5\n例3：一质点运动轨迹为抛物线求：x=-4m时（t>0)粒子的速度、速率、加速度。xy(SI)(SI)解：练习\nhxl例4如图，在岸上以速率v0将水面上的船拉回岸边，设水面离岸上滑轮h高，求船离岸水平距离x时的速度。xoy解：建立如图的坐标系，设船离岸水平距离x时绳长为l，绳与水面夹角为。由几何知识，负号表示船的运动与x轴反向，即水平指向岸边。\nhsl\n例题5.一气球以速率v0从地面上升,由于风的影响,随着高度的上升,气球的水平速度按vx=By增大,其中B是正的常量,y是从地面算起的高度,x轴取水平向右的方向.(1)求气球的运动方程;(2)求气球水平飘移的距离与高度的关系.解:取如图坐标系,yxO已知vy=v0,vx=By则所以y=v0t令t=0时气球位于坐标原点而那么积分后运动方程为:x与y的关系\n例6.如图所示,A﹑B两物体由一长为l的刚性细杆相连,A、B两物体可在光滑轨道上滑行.如物体A以速率v向左滑行.当为60°时,物体B的速度为多少.解:坐标系如图.物体A的速度物体B的速度为对三角形OAB有两边微分有物体B速度为方向沿y轴正向.当=60°时解(1)由定义得(2)已知运动参数方程x=2t消去t得:当t=2s时曲线为开口向下的抛物线.y=6–2t2y=6x2/2例7.设质点的运动方程为(1)求t=2s时的速度.(2)作出质点的运动轨迹图.(SI)(m/s)xy055BxyOlA\n例题8.有一个球体在液体中竖直下落,球体的初速为,它在液体中的加速度为.问球体在停止前运动的路程有多长?解1:先求运动方程再得结论得有又由速度的定义球体停下来,即v=0.由速度表达式知t=∞此时x=10m事实上,只要时t≈10s,球体已几乎不再运动.解2.直接求v与x的关系已知球体作变加速直线运动\n1-3、圆周运动一、圆周运动的角量描述OXR角位移沿逆时针转动，角位移取正值沿顺时针转动，角位移取负值角位置（一）.极坐标系极点O，极轴X，角位置\n（二）定义角速度单位：rad/s角速度等于角位置对时间的一阶导数（三）定义角加速度单位：rad/s2角加速度等于角速度对时间的一阶导数或角位置对时间的二阶导数匀速圆周运动匀变速圆周运动是恒量是恒量\n二、切向加速度和法向加速度在轨道曲线上任取一点为坐标原点，以“弯曲轨道”作为坐标轴。P处的坐标即为轨道的长度s(自然坐标)运动方程方向描述作相互垂直的单位矢量切向单位矢量法向单位矢量指向轨道的凹侧1.自然坐标系\nC2.曲线运动速度增量取由于速度大小不同而引起的速度变化由于速度方向改变而引起的速度变化\n沿A点的法线方向(平行)沿A点的切线方向(平行)切向加速度由于速度大小变化而产生的，沿切线方向法向加速度由于速度方向变化而产生的，沿法线方向\n切向加速度大小等于速度的大小(或速率)对时间的导数，方向沿轨道的切线方向。法向加速度大小等于速率平方除以曲率半径，方向沿轨道的法线指向。\n加速度总是指向曲线的凹侧3.圆周运动中的切向加速度和法向加速度曲率半径是恒量匀速圆周运动向心加速度线量速度、加速度角量角速度、角加速度4.角量与线量的关系\n1.由楼窗口以水平初速度v0射出一发子弹，取枪口为原点，沿v0为x轴，竖直向下为y轴，并取发射时t=0.试求：(1)子弹在任一时刻t的位置坐标及轨道方程；(2)子弹在t时刻的速度，切向加速度和法向加速度。anagyxov0解：(1)例题(2)与切向加速度垂直与速度同向\n2.一质点在oxy平面内作曲线运动，其加速度是时间的函数。已知ax=2,ay=36t2。设质点t＝0r0=0,v0=0。求：(1)此质点的运动方程；(2)此质点的轨道方程，(3)此质点的切向加速度。解：\n所以质点的运动方程为：(2)上式中消去t,得y=3x2即为轨道方程。可知是抛物线。\n例3.一气球以恒定速率v0从地面上升,由于有风,随高度上升,气球水平速度按vx=By增大(B为正常量),y是从地面算起的高度,取水平向右为x正向.求:(1)气球的运动方程;(2)气球水平飘移的距离与高度的关系;(3)气球沿轨道运动的切向加速度和轨道的曲率半径与高度的关系.解:坐标如图.t=0时气球在原点.y=v0t而vx=(1)运动方程为:(2)x与y的关系vy=yxOx=Bv0t2/2y=v0t(3)v=(vx2+vy2)1/2=(B2v02t2+v02)1/2at=dv/dt=B2v02t/(B2v02t2+v02)1/2an=(a2at2)1/2=(ax2+ay2at2)1/2=Bv02/(B2y2+v02)1/2r=v2/an=(B2y2+v02)/{Bv02/(B2y2+v02)]1/2}=(B2y2+v02)1/2/(Bv02)=[B2v02+02B4v02y2/(B2y2+v02)]1/2=B2v0y/(B2y2+v02)1/2=(B2y2+v02)1/2例4.一物体在x轴上运动,加速度满足a=kv,经过坐标原点时速度为v0.求速度v与坐标x的函数关系.解a=dv/dt=(dv/dx)(dx/dt)=vdv/dx)=kvdv/dx=kv=v0kx\n角速度方向规定为沿轴方向，指向用右手螺旋法则确定。加速转动方向一致减速转动方向相反角速度矢量的方向角速度与线速度的矢量关系\n1-4相对运动运动描述具有相对性车上的人观察地面上的人观察静止参考系（地）绝对运动(球对地)牵连运动(车对地)相对性运动参考系（车）相对运动(球对车)\n位矢位矢O′相对于O点的位矢xyOy′O′x′位移位移t时间内原点O′相对于原点O的位移为\nO′相对于O点的速度牵连速度O′相对于O点的加速度质点在S系中的速度、加速度绝对速度质点在S′系中的速度、加速度相对速度A,B,C三个质点相互间有相对运动伽利略变换式\n当两参照系相对做匀速直线运动，X轴重叠时二、伽利略变换式\n三、经典时空观根据伽利略变换，我们可得出牛顿的绝对时空观，也称之为经典时空观在S系内，米尺的长度为在S’系内，米尺的长度为利用伽利略变换式得结论：空间任意两点之间的距离对于任何的惯性系而言都是相等的，与惯性系的选择或观察者的相对运动无关，也就是说，长度是“绝对的”，或称之为“绝对空间”\n再有表明：时间也是与惯性系的选择或观察者的相对运动无关的“绝对空间”、“绝对时间”和“绝对质量”这三个概念的总和构成了经典力学的所谓“绝对时空观”：空间、时间和物质的质量与物质的运动无关而独立存在，空间永远是静止的、同一的，时间永远是均匀地流逝着的。\n如果把随惯性系而变的看成是“相对”的，那么经典力学中：时间、长度、质量“同时性”和力学定律的形式物体的坐标和速度“同一地点”是相对的是绝对的把不随惯性系而变的看成是“绝对”的，\n近代物理学发展表明：经典的、与物质运动无关的绝对时空观是错误的，并揭示出时间、空间与物质运动密切相关的相对性时空观；而力学相对性原理则得到改造发展为物理学中更为普遍的相对性原理\n1.河水自西向东流动，速度为10km/h,一轮船在水中航行，船相对于河水的航向为北偏西30o,航速为20km/h。此时风向为正西，风速为10km/h。试求在船上观察到的烟囱冒出的烟缕的飘向。（设烟离开烟囱后即获得与风相同的速度）解：设水用S；风用F；船用C；岸用D已知：正东正西北偏西30o例题vcsvfcvfdvsdvcd\n方向为南偏西30o。vcsvfcvfdvsdvcd\n2.一男孩乘坐一铁路平板车，在平直铁路上匀速行驶，其加速度为a，他沿车前进的斜上方抛出一球，设抛球时对车的加速度的影响可以忽略，如果使他不必移动他在车中的位置就能接住球，则抛出的方向与竖直方向的夹角应为多大？aV0解：抛出后车的位移：球的位移：\n小孩接住球的条件为：x1=x2;y=0两式相比得：