大学物理第-章 154页

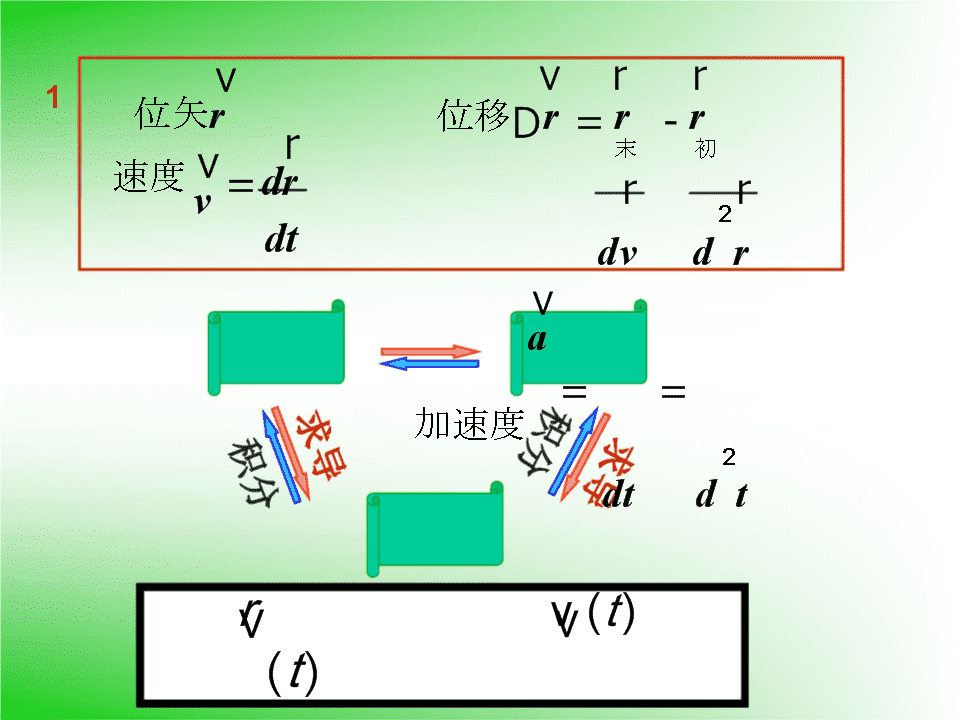
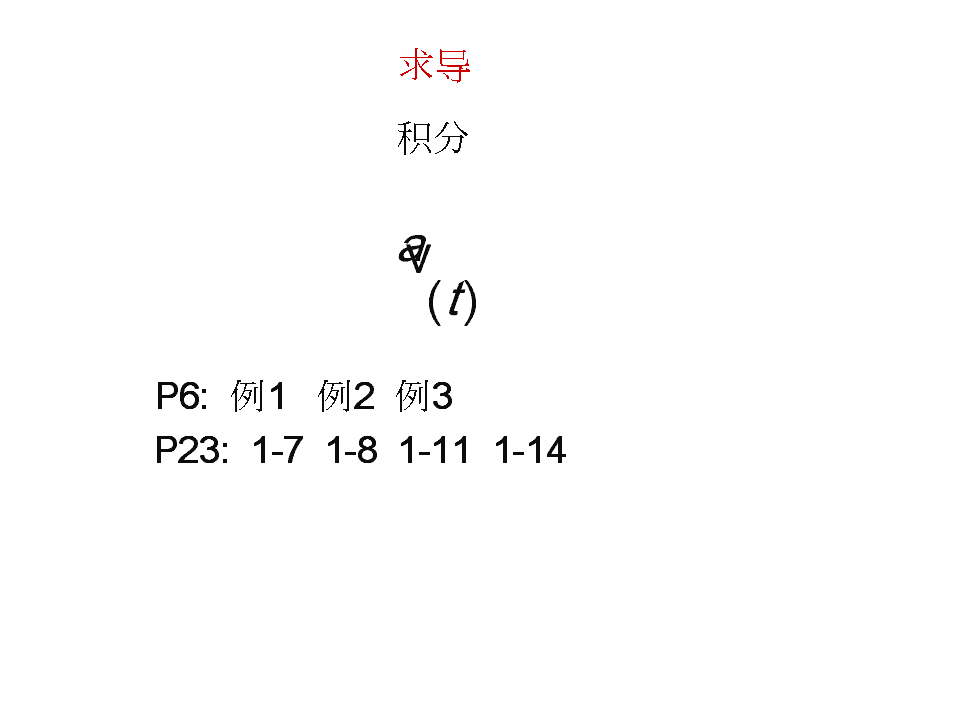
第一章质点运动学\n1v位矢r速度vv=rdrdtvrr位移Dr=r-r末初rr2dvdrva==加速度2dtdtrvvv(t)(t)\n求导积分av(t)P6:例1例2例3P23:1-71-81-111-14\n特别指出无论是求导还是积分的过程,针对的都只是时间t,即只有量值含有时间变量t,才能直接求导或积分;不含有时间t项,应做适当的处理.rvvv):分离变量再积分a=a(rrrr\nvvrdrrvvddvvr)d=v=\na=a (:a r=rdtdrdrdt\n2线量角量vrq(t)vrrD=-rrr末初Dq=q-q末初vv=rdrdtv=rww=dqdt\nvarr2dvdr==2dtdta=w2rna=artw2qdda==2dtdt\n3a=+ateaentndvar==atdt2var==wnr2注意\n公式中所涉及的v是速率,并非速度.vdvdvvaa==tdtdt\n例一质点沿半径为R的圆周运动，其路程S随时1S=-2间t变化的规律为btct(SI)，式中b、c2为大于零的常量，且b2>Rc．则此质点运动的切向-c(b-ct)2/R加速度at=_____；法向加速度an＝_____________．an=2vrv=dsdt\nat=dvdt\nrr rr=Rwti+Rwtjcossin例质点运动方程rrrv=-wRsinwti+wRcoswtj(R，w是常数)，_________________________，0dv¤dt=___________________，x2+y2=R2质点的轨道方程为______________。\n\nvF=mvdvdt=vmarvvv(t)(t)求导积分av(t)\nP39:例2例3例5P23:2-192-22\n\n1力的时间累积效应vvvvvtÞò=-Ft=mdd(v)Fdtmvmv221t1ì=DIpßrvì=tò2ïIFdtít1rvvï=pmî\nïxxrvíIp=DIp=Dyyï=DIpîßzzvvvvFex=0Fex<(H)(O)\npv2p2o12000vms/×-\vp=(H)2000m/sv(H)(O)322Mp2=2==4\nv\vp(O2)=500m/s(O)M(H)2p22\nP20912-14如图两条曲线分别表示氢气和氧气在同一温度下的麦克斯韦速率分布曲线，从图上数据求：(1)氢气和氧气的最可几速率；(2)温度；(3)若曲 线分别表示氢气在不同温度下的麦克斯韦速率分布 曲线，那么哪一条曲线的气体温度高？f(v)vp=2RTMp(H2)=2000m/svo2000/×-1vmsvM2pH2(2)T=4.8110\nK=´22R(3)兰色曲线的气体温度高.\n开尔文卡诺克劳修斯\n1能分析计算理想气体在等体、等压、等温和绝热过程中的热量、功和内能的改变量.iC=RQC(TT)=n- ìVm,2VV,m21（1）Q=nCm(T2-T1)í=-C=C+RQC(TT)n\nîPPmpmVm,21,,2W=òpdVg=功的大小等于p-V图上CCp,mV,m1过程曲线下的面积！iDE=nRT-T()21\n2Q=DE+W （2）pV=nRT（3）\n过程过程特点过程方程功Ｗ内能增量等体dV=0PT=C0DE=nCT-TVm,(21)等压dP=0VT=CWP(VV)=-21=n-R(TT)21DE=nCT-TVm,(21)dT=PV=C0等温WRT=n=nRTlnlnP1P2VV210\n绝热dQ=0PVg=C1TVg-=C12Pg-T-g=C13WE=-D=-n-C(TT)V,m21PVPV-=1122g-1DE=nCT-TVm,(21)\n功Ｗ内能增量过程热量Ｑ摩尔热容等体0DE=nCT-TVm,(21)Q=nCT-TVVm,(21)iC=RVm,2等压WP(VV)=-21=n-R(TT)21DE=nCT-TVm,(21)Q=nCT-Tppm,(21)i2+CR=P,m2WRT=n=nRTlnlnP1P2V2V1\n0¥Q=W等温绝热WE=-D=-n-C(TT)V,m21PVPV-=1122g-DE=nCT-TVm,(21)00\n1\n2能分析计算理想气体在循环过程中的热量、DE=0功和内能的改变量以及效率.hQQQ-W==吸放=-放1QQQ吸吸吸W=Q=Q-Q吸放pp1A\npp24p3oT1BWDCTV2VV4V2V31h=-1卡T2T1\n例1mol双原子分子理想气体经如图的循环过程，其中1－2为直线，2－3为绝热线，3－1为等温线．已知T2=2T1，V3=8V1试求：(1)各过程的功，内能增量和传递的热量；(用T1和已知常量表示)(2)此循环的效率h．pp22解：(1)1－2:1W=pV-pV()12221121=n-R(TT)212==1252RT1RT11p13OVV2V1V3\niDE=nRT-T12(21)25=-R(2TT)11251Q=DE+W=RT+RT=RT312121211122\n例1mol双原子分子理想气体经如图的循环过程，其中1－2为直线，2－3为绝热线，3－1为等温线．已知T2=2T1，V3=8V1试求：(1)各过程的功，内能增量和传递的热量；(用T1和已知常量表示)(2)此循环的效率h．pp222－3绝热膨胀过程:p11Q=230W=-DE23233OVV2V1V3\n5=-n-R(TT)3225=--R(TT)122=52RT1\n例1mol双原子分子理想气体经如图的循环过程，其中1－2为直线，2－3为绝热线，3－1为等温线．已知T2=2T1，V3=8V1试求：(1)各过程的功，内能增量和传递的热量；(用T1和已知常量表示)(2)此循环的效率h．p3－1等温压缩过程:D=E310Q=W3131p2p11231V=ò=òdVVOVV2V1V\npdVRT1n13V33=-=-RT1ln82.08RT1\n解：(1)1－2:p51Q=DE+W=RT+RT=RT312121211122p222－3绝热膨胀过程:Q=2301p13OVV2V1V33－1等温压缩过程:Q=W31311V=ò=òpdVRTdVV=-=-RTRT1ln82.08\n1n13V31(2)此循环的效率Q2.08h=-31=-=1130.7%Q312\n第十三章热力学基础习题答案13-24如图所示是某单原子理想气体循环过程的V-T图，图中VC=2VA，试问：(1)图中所示循环是代表致冷机还是热机？(2)如果是正循环(即热机循环)，求出循环效率.PPAABVVCCBCVAAOVAVCVOT\n(1)图中所示循环代表热机.\n第十三章热力学基础习题答案5Q=nCT-T=nRT()ABp,mBAA23Q=nCT-T=-nRT()BCV,mCBA2AòQWpdV==CACACPPAABC\nhdVVò=n=-nARTRTln2AAVVCQQ-W==吸放QQ吸吸QQQ2(1ln2)12.3%OVAVCVC=2VATC=TATB=2TAV\n++-===ABBCCAQ5AB\n3理解热力学第二定律的含义.例根据热力学第二定律可知：(A)功可以全部转换为热，但热不能全部转换为功．(B)热可以从高温物体传到低温物体，但不能从低温物体传到高温物体．(C)不可逆过程就是不能向相反方向进行的过程．(D)一切自发过程都是不可逆的．［D］\nA例根据热力学第二定律（）(A)自然界中的一切自发过程都是不可逆的(B)不可逆过程就是不能向相反方向进行的过程(C)热量可以从高温物体传到低温物体，但不能从低温物体传到高温物体(D)任何过程总是沿着熵增加的方向进行\n第十四章相对论specialrelativity\n1理解狭义相对论的两条基本原理.相对性原理物理定律在所有惯性系中都具有相同的表达形式.光速不变原理真空中的光速是常量，沿各个方向都等于c，与光源或观测者的运动状态无关，即不依赖于惯性系的选择.\n2掌握洛伦兹的坐标变换式.b=vg=-bc112洛伦兹坐标变换式正变换x¢=g-v(xty¢=z¢=yzv)x)逆变换x=g¢+v¢y=¢(xt)yz=¢z\n¢gt(t=-2cvt=¢+¢g(tx2c)\n3理解同时的相对性、长度收缩和时间延缓的概念，掌握狭义相对论的时空观.会分析计算有关同时的相对性、长度收缩和时间延缓的问题．\n同时性具有相对意义vΔtΔx-2cΔt'=-b21沿两个惯性系运动方向，不同地点发生的两\n个事件，在其中一个惯性系中是同时的，在另一惯性系中观察则不同时，所以同时具有相对意义；只有在同一地点，同一时刻发生的两个事件，在其他惯性系中观察也是同时的.\n长度量度的相对性(动尺收缩)D-DDxutx¢D===gDxx22uu11--22cc\nszoysz'o'y'vvlxx'2'01'xx12xx'\n例1设想有一光子火箭，相对于地球以速v0.95c=率飞行，若以火箭为参考系测得火箭长度为15m，问以地球为参考系，此火箭有多长？yy'0=loo'15mvvx'xs's火箭参照系地面参照系\n解：固有长度l0=15m=l'l=l-bl=151-0.952m=4.68m201\no'x'y'例2一长为1m的棒静止地放在平面内，S'oo'x'45在系的观察者测得此棒与轴成角，试问从S系的观察者来看，此棒的长度以及棒与ox轴的夹角是多少？设想系相对S系的运动速度v=3c2.S'yy'oo'lvv'y'q''lx解：在S'系q'=45o,l'=1ml'==y'2/2m\nx'x''xl'在S系l=yl'2/y'=2ml=l'¢-v/c=/124m22xxl=2+=2y\nq==»lxlarctanarctan263.43l0.79moylx\n例一隧道长为L，宽为d，高为h，拱顶为半圆，如图所示．设想一列车以极高的速度v沿隧道长度方向通过隧道，若从列车上观察:(1)隧道的尺寸如何?(2)设列车的长度为l0，它全部通过隧道的时间是多少?解(1)根据相对论效应，从列车上观察，隧道长度缩短，其它尺寸不变，长度变为hd/2L'=1-Lvc22dL\n(2)从列车上观察，隧道以速率v经过列车，全部通过所需时间为Dt¢=¢Lv+l0v=L2v1-+2cvl0d/2hL d\n时间延缓效应(动钟变慢)u¢¢D+DD¢tcxt2D=-===gDtttt 21220 uu11--22cc\nyvvy's'soo'dB91263xx'ysx1o1293d912693x2x12366\n例在6000m的高空大气层中，宇宙射线产生μ子，μ子是物理性质与电子类似的粒子，质量是电子质量的206.768倍，其速率0.998c，其静止时的寿命2×10-6s.根据经典力学理论：μ子的行程d=vt=c´´-=m6000.998210599μ子不能穿过大气层到达地球表面！\n例在6000m的高空大气层中，宇宙射线产生μ子，μ子是物理性质与电子类似的粒子，质量是电子质量的206.768倍，其速率0.998c，其静止时的寿命2×10-6s.根据时间延缓理论：μ子的寿命t=1t0-vc22=3.16´10-s5d=vt=´3m9.4610μ子的行程μ子能够穿过大气层到达地球表面！\n实验结果的确如此！\n例在6000m的高空大气层中，宇宙射线产生μ子，μ子是物理性质与电子类似的粒子，质量是电子质量的206.768倍，其速率0.998c，其静止时的寿命2×10-6s.根据长度收缩理论：地球：固有长度L0=6000mμ子：运动长度2v¢=-=379.3mLL012\ncd=vt=c´´-=m6000.998210599μ子能够穿过大气层到达地球表面！\n4掌握狭义相对论中质量与速度的关系，以及质量与能量间的关系.(1)相对论质量mm==gm0021-bE=mc2(2)相对论能量\n(3)相对论动能E=mc2-mc2k0\n例根据相对论力学，动能为0.25MeV的电子，其运动速度约等于(A)0.1c(B)0.5c(C)0.75c(D)0.85cC［］(电子的静能m0c2=0.51MeV)E=mc-mc22k0E=g-mc(1)2mm==gm00b21\nk0-g=1-21(v/c)\n例观察者甲以0.8c的速度（c为真空中光速）相对于静止的观察者乙运动，若甲携带一质量为1kg的物体，则9×1016J(1)甲测得此物体的总能量为____________；1.5×1017J(2)乙测得此物体的总能量为____________．甲测得此物体的总能量E=mc002乙测得此物体的总能量\n11=2=2=EmcmcE00-2-21(v/c)1(v/c)\n例匀质细棒静止时的质量为m0，长度为l0，当它沿棒长方向作高速的匀速直线运动时，测得它的长为l，那么，该棒的运动速度v=____c____-__l_l_______，该棒所具有的动能1(/)20ll-20mcl0()EK=_________________．=-v2ll012c\n122E(1)mc(1)mc=g-=-k0201(v/c)-