大学物理一-8 7页

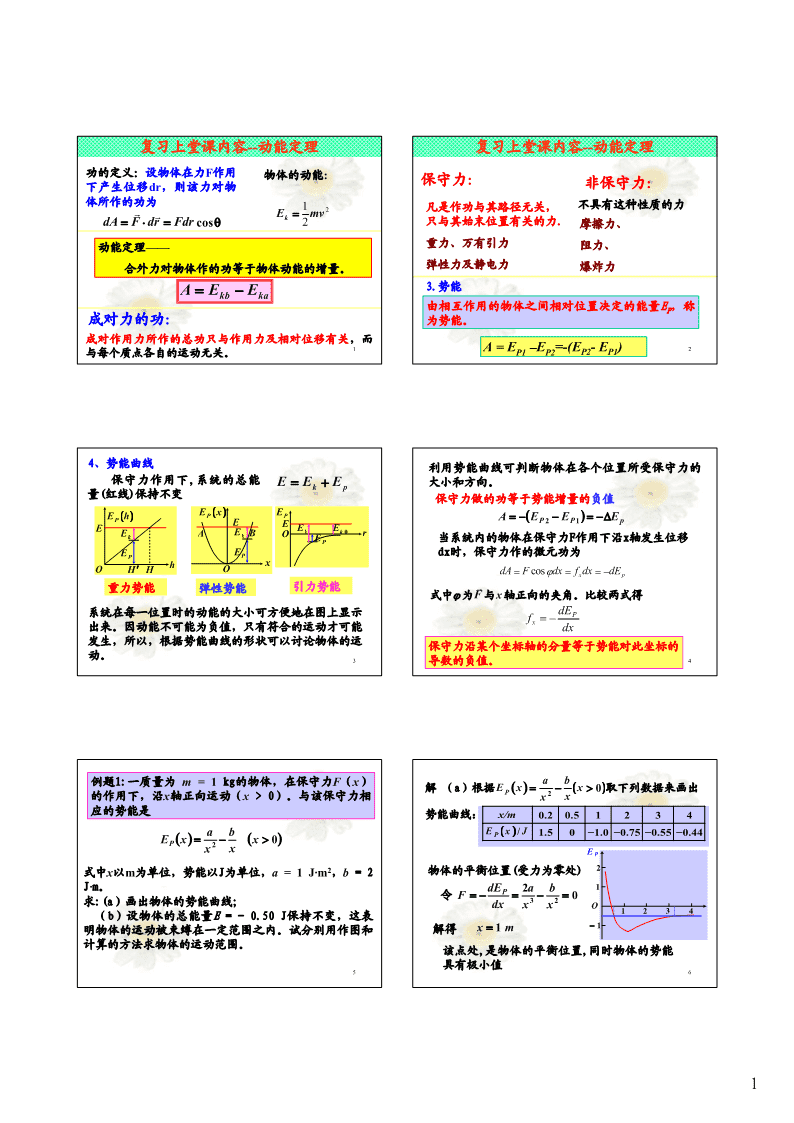
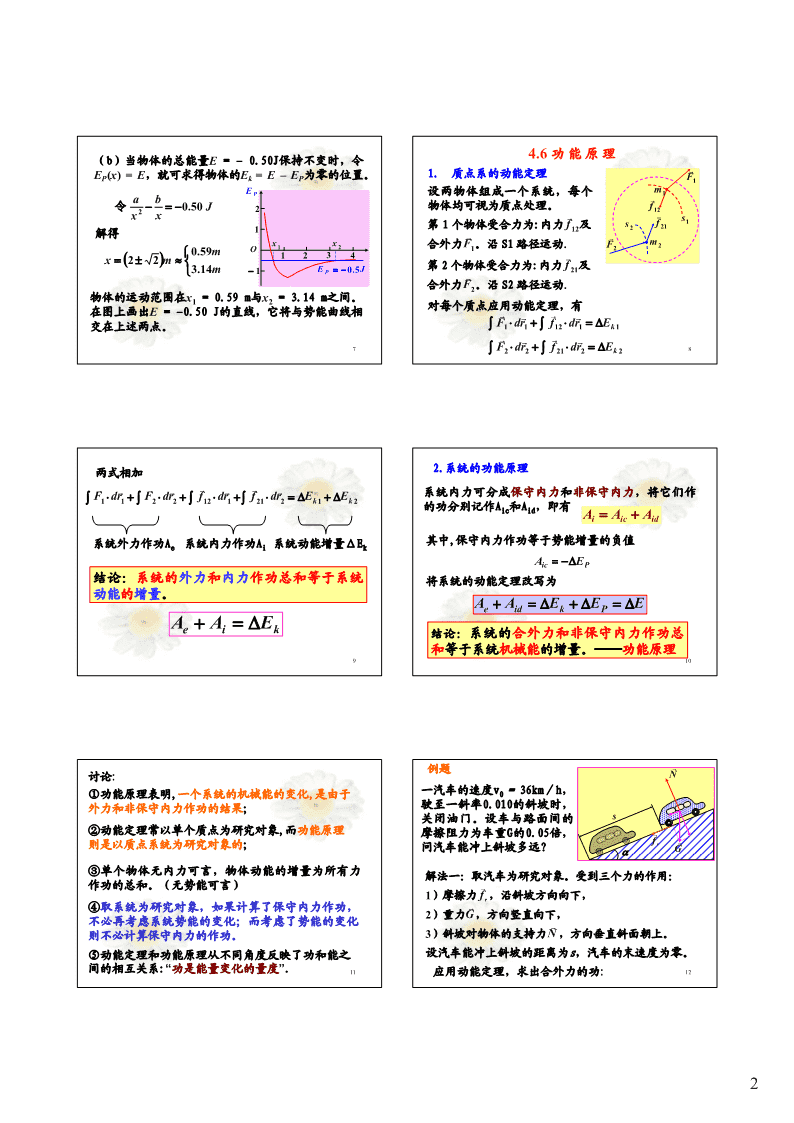
复习上堂课内容--动能定理复习上堂课内容--动能定理功的定义：设物体在力F作用物体的动能:保守力:非保守力:下产生位移dr，则该力对物体所作的功为12凡是作功与其路径无关，不具有这种性质的力rrEk=mvdA=F⋅dr=Fdrcosθ2只与其始末位置有关的力.摩擦力、动能定理——重力、万有引力阻力、合外力对物体作的功等于物体动能的增量。弹性力及静电力爆炸力A=E−E3.势能kbka由相互作用的物体之间相对位置决定的能量E，称P成对力的功:为势能。成对作用力所作的总功只与作用力及相对位移有关，而与每个质点各自的运动无关。1A=EP1–EP2=-(EP2-EP1)24、势能曲线利用势能曲线可判断物体在各个位置所受保守力的保守力作用下,系统的总能E=E+E大小和方向。kp量(红线)保持不变保守力做的功等于势能增量的负值EP(h)EP(x)EPA=−(EP2−EP1)=−ΔEpEEEEAEBOEkEk0rkkE当系统内的物体在保守力F作用下沿x轴发生位移PEPEPdx时，保守力作的微元功为hxOH′HOdA=Fcosϕdx=fdx=−dExp重力势能弹性势能引力势能r式中ϕ为F与x轴正向的夹角。比较两式得系统在每一位置时的动能的大小可方便地在图上显示dEPf=−x出来。因动能不可能为负值，只有符合的运动才可能dx发生，所以，根据势能曲线的形状可以讨论物体的运保守力沿某个坐标轴的分量等于势能对此坐标的动。3导数的负值。4例题1:一质量为m=1kg的物体，在保守力F（x）ab解（a）根据EP()x=2−(x>0)取下列数据来画出的作用下，沿x轴正向运动（x>0）。与该保守力相xx应的势能是势能曲线：x/m0.20.51234abEP(x)/J1.50−1.0−0.75−0.55−0.44EP()x=2−()x>0xxEP式中x以m为单位，势能以J为单位，a=1J·m2，b=2物体的平衡位置(受力为零处)2J·m。dEP2ab1令F=−=−=0求:(a）画出物体的势能曲线；dxx3x2O1234（b）设物体的总能量E=-0.50J保持不变，这表明物体的运动被束缚在一定范围之内。试分别用作图和解得x=1m−1计算的方法求物体的运动范围。该点处,是物体的平衡位置,同时物体的势能具有极小值561\n4.6功能原理（b）当物体的总能量E=−0.50J保持不变时，令1.质点系的动能定理rEP(x)=E，就可求得物体的Ek=E–EP为零的位置。F1EP设两物体组成一个系统，每个m1abr令2−=−0.50J2物体均可视为质点处理。f12xxrrssf11第1个物体受合力为:内力f12及221解得rrx1x2合外力F1。沿S1路径运动.F2m2⎧0.59mO1234rx=()2±2m≈⎨第2个物体受合力为:内力f及⎩3.14m−1EP=−0.5Jr21合外力F2。沿S2路径运动.物体的运动范围在x1=0.59m与x2=3.14m之间。对每个质点应用动能定理，有在图上画出E=−0.50J的直线，它将与势能曲线相rrrr交在上述两点。∫∫F1⋅dr1+f12⋅dr1=ΔEk1rrrr7∫∫F2⋅dr2+f21⋅dr2=ΔEk282.系统的功能原理两式相加∫∫Fr⋅drr+∫∫Fr⋅drr+fr⋅drr+fr⋅drr=ΔE+ΔE系统内力可分成保守内力和非保守内力，将它们作1122121212k1k2的功分别记作Aic和Aid，即有Ai=Aic+Aid系统外力作功A系统内力作功A系统动能增量ΔE其中,保守内力作功等于势能增量的负值eikAic=−ΔEP结论：系统的外力和内力作功总和等于系统将系统的动能定理改写为动能的增量。Ae+Aid=ΔEk+ΔEP=ΔEA+A=ΔEeik结论：系统的合外力和非保守内力作功总和等于系统机械能的增量。──功能原理910例题r讨论:N①功能原理表明,一个系统的机械能的变化,是由于一汽车的速度v0=36km／h，外力和非保守内力作功的结果;驶至一斜率0.010的斜坡时，关闭油门。设车与路面间的s②动能定理常以单个质点为研究对象,而功能原理摩擦阻力为车重G的0.05倍，r则是以质点系统为研究对象的;问汽车能冲上斜坡多远？frrαG③单个物体无内力可言，物体动能的增量为所有力解法一：取汽车为研究对象。受到三个力的作用：作功的总和。（无势能可言）r1）摩擦力fr，沿斜坡方向向下，④取系统为研究对象，如果计算了保守内力作功，r2）重力G，方向竖直向下，不必再考虑系统势能的变化；而考虑了势能的变化r则不必计算保守内力的作功。3）斜坡对物体的支持力N，方向垂直斜面朝上。⑤动能定理和功能原理从不同角度反映了功和能之设汽车能冲上斜坡的距离为s，汽车的末速度为零。间的相互关系:“功是能量变化的量度”.11应用动能定理，求出合外力的功:122\n支持力N不作功1解法二：取汽车和地球为研究系统，汽车受到的外力2−fs−Gssinα=0−mv（1）r0为摩擦力和支持力，支持力不作功，应用功能原理摩擦力和重力在2（外力作功等于系统机械能的增量A=E2-E1）斜面方向作的功：fNGr==μμαcos代入（1）得⎛12⎞rr−frs=()0+Gssinα−⎜mϖv0+0⎟NN⎝2⎠12即1μGscosα+Gssinα=mv0（2）μGs=mϖv2−Gssinα20（4）ss2rr由于tanα=0.010很小,同样解得frfrrv2rGαGs=ϖ00=85mαsinα≈tan,cosαα≈12g()μ+tanα故有μgs+gstanα=1v2（3）解法二说明，汽车在上坡前动能和势能（设为零）02的总和大于上坡后动能（为零）和势能的总和，汽2车在上坡中机械能减少了，它所减小的能量等于反vs=0=85m得()抗摩擦力所作的功。2gμ+tanα1314例题AO§4.6机械能守恒定律能量守恒定律一个质量m=2kg的物体从静rθfr系统的功能原理r止开始，沿四分之一的圆周从NA滑到B。已知圆的半径R=rAe+Aid=ΔEk+ΔEP=ΔErϖ4m，设物体在B处的速度v=6mG1.机械能守恒定律／s，求在下滑过程中，摩擦B力所作的功。如果一个系统内只有保守力作功，其他内力和一切解：物体受三个力：重力、摩擦力及正压力，外力都不作功，或者它们的总功为零，则系统内物体的动能和势能可以互相转换，但机械能的总值不重力为保守力，正压力不作功。变。这个结论叫做机械能守恒定律应用功能原理，摩擦力作功等于物体机械能的增量.1用数学表示式表示为2A=EB−EA=mϖv−mgR=−42.4J2当Ae+Aid=0时，ΔE=0负号说明摩擦力作负功，或物体克服摩擦力作功。15则E＝E=……=常量16BA2.讨论:解题时注意：①总对一个确定的系统和一个确定的过程而言;1.选定系统；②应用条件:在整个过程中外力和非保守内力作功的2.分析受力（是否保守系统）；代数和为零;3.确定势能零点位置（重力势能、弹力势能）；③保守系:相互间只有保守力作用的系统;4.选定初、末位置，写出相应的机械能表达式；④推广:能量守恒与转换定律.运用相应的功能关系求解。──自然界普遍遵循的基本规律.一个不受外界作用的系统叫做孤立系统。对于孤立系统，经历任何变化时，该系统的所有能量的总和是不变的，能量只能从一种形式变化为另一种形式，或从系统内一个物体传给另一个物体。17183\n例1起重机用钢丝绳吊运一质量为m的物体，以速度rTv0作匀速下降，当起重机突然刹车时，物体因惯性继续下降，问使钢丝绳再有多少微小的伸长？（设解:由物体、地球和钢丝钢丝绳的劲度系数为k，钢丝绳的重量忽略不绳所组成的系统，除重力和计）．这样突然刹车后，钢丝绳所受的最大拉力将钢丝绳中的弹性力外，其它x0有多大？的外力和内力都不作功，所hr以系统的机械能守恒。Trmg设最低点h处（结束位置）系统的动能、重力势能x0均为零hv0rmg1920初始位置1：（起重机突然停止的那个瞬时位置），rr结束位置2：（物体最低处）TT物体的动能为12Ek1=mv0系统的动能、重力势能均为2零，仅有弹性势能，即设此时钢丝绳的伸长量x0，xx001h弹12h系统的弹性势能为E弹=kx2E2=EP2=k()x0+hP1202rrmgmg系统的重力势能为E重=mghP1此时（初始位置）系统的总机械能为弹重1212E=E+E+E=mv+kx+mgh1k1P1P100222122rTx由机械能守恒rxxFx2121212m0mvϖ0+kx0+mgh=k()x0+h1Ox1222x0h物体作匀速运动时钢丝绳的伸长量满足rmgGmgm2T=kx0=mg,x0==kk例题2用一弹簧将质量分别为m1和m2的上下两水代入上式解得平木板连接如图，下板放在地面上，（1）如以上板mh=ϖv在弹簧上的平衡静止位置为重力势能和弹性势能的零0k点，试写出上板、弹簧以及地球这个系统的总势能。钢丝绳的最大受力（2）对上板加多大的向下压力F，才能因突然撤去⎛mgm⎞Tm′=k()x0+h=k⎜+ϖv0⎟=mg+kmϖv0它，使上板向上跳而把下板拉起来？⎝kk⎠23244\nxrxxFx2取平衡静止位置时重力势能为零。0m1xO1则系统的重力势能为EPg=m1gx系统的总势能为12EP=EPe+EPg=kx−kx0x+m1gx2m2(a)(b)(c)(d)考虑到平衡条件kx0=m1g解（1）取上板的平衡位置为x轴的原点（图a）。设弹簧原长时上板在坐标轴的x0处。12代入上式,得E=kxp图（a）时弹簧压缩x0，图（b）时弹簧伸长x-x02则任意x位置时系统的弹性势能为从这里看到，选上板在弹簧上静止的平衡位置为原121212点和势能零点，系统的总势能以弹性势能的单一形EPe=k()x−x0−kx0=kx−kx0x式出现。2222526（2）在弹簧上加力F时，弹簧由平衡位置压缩xrxxFx2x1,物体静止，此时系统为初态m01Ox112Ek1=0，EP1=kx12撤去外力F时,弹簧由平衡位置伸长最大x,m22物体静止,此时系统为末态12由于恰好提起m2时有k(x2−x0)=m2gE=0，E=kxk2P222由已知条件有kx=mgkx=F011外力使弹簧下压x1，弹簧潜在的能量使得撤去外力后反弹x2,,两者能量转换。解得F=(m1+m2)g1212系统的机械能守恒得kx1=kx2⇒x1=x2因此，下板能被拉起的条件是2227F≥(m1+m2)g28例3.一弹簧,原长为l0,劲度系数为k,上端固定,下端解:(1)设物体处在平衡位置时,弹簧的静伸长量为x0.挂一质量为m的物体,先用手托住,使弹簧不伸长.(1)取坐标Ox向下为正,以平衡位置为坐标原点.如将物体托住慢慢放下,达静止(平衡位置)时,弹簧的最大伸长和弹性力是多少？(2)如将物体突然放手,由受力平衡−kx+mg=0物体到达最低位置时,弹簧的伸长和弹性力各是多0少？物体经过平衡位置时的速度是多少？mg得x0=k分析:物体悬挂于弹簧下端,受重力和弹性力作用.取物体,弹簧和地球为系统时,,Ae+Aid=0此时,弹簧作用于物体的弹性力大小为所以,系统的机械能守恒.弹性势能零点通常选在弹簧的原长处.平衡位置是物体受合外力为零的位置,F=kx=mg对应系统势能的最小值.029305\n(2)突然放手后,设物体最低可到达x.以“放手”位置和设物体在平衡位置时的速度为v,x处为系统的始末态,此过程系统的机械能守恒.选平仍由机械能守恒定律衡位置为重力势能零点,弹簧原长处为弹性势能零点.则有11212mgx=−mgx+k(x+x)2mgx=kx+mv00020222mg得弹簧的伸长量为x+x=0k得mv=g=gx弹性力大小为F=k(x+x)=2mgk00同理，把同一物体突然放下（称突加载荷）所引起的最大压缩量是缓慢放下（称静载荷）使物体达到静平衡时所引起的最大压缩量的2倍，这就是许多工程问题中要尽量避免突加载荷的原因。3132课堂练习:2．如图所示。桌面固定不动，mvv0∫F⋅dr=0与桌面间摩擦系数为μ，弹簧的1.保守力的特点，劲度系数为k，开始时m静止于原0A=−ΔE保守力的功与势能的关系是保p。点O。当把m轻轻挂上，使m0运动，在m下降一段距离d的过程中，按功能原理分别写出下列不同物体系统的功能关系（忽略绳和滑轮的质量以及它们之间的摩112(1)以m擦）。、m为系统，功能关系为mgd−−=+kdμmgd00；()mmv0221122mgd−−=+kdμmgd()mmv0022(2)以m、k、m为系统，功能关系为；01122−=+−+μmgd()mmvmgdkd00332234(3)以m、k、m、地球为系统，功能关系为。0§4.8碰撞二、两球的正碰撞（对心碰撞）一、碰撞一、碰撞1、定义：1、概念:两个或两个以上的物体相遇，且如果两球在碰撞前的速度在两球的中心连线相互作用持续一个极短暂的时间——碰撞。上，则碰撞后的速度也都在这一连线上，这种狭义：接触，速度变化，能量转换。碰撞称为对心碰撞（正碰撞）。例：桌球、滑块、交通事故等；vvvvvvvv102012广义：接近，短暂互作用，偏离原运动方向。rr例：分子原子、α粒子、核反应等。又称散射。F12F212、特点m1m2m1m2m1m2•物体间的相互作用是突发性，持续时间极短,内力>>外力。碰撞前碰撞时碰撞后•作用力峰值极大，碰撞符合动量守恒定律。•碰撞过程中物体会产生形变。35366\n4、碰撞分类2、动量守恒方程mv+mv=mv+mvLL(1)1102201122⑴若e=1，则分离速度等于接近速度，无动能损失，称完全弹性碰撞；3、恢复系数（牛顿碰撞定律）碰后分离速度v−v⑵若e=0，则碰后以共同速度运动，动能损失e==21LL(2)碰前趋近速度v−v最大，称完全非弹性碰撞；1020注：斜碰时分离速度与接近速度指沿碰撞接触处⑶一般地，0