大学物理-波动-djh 72页

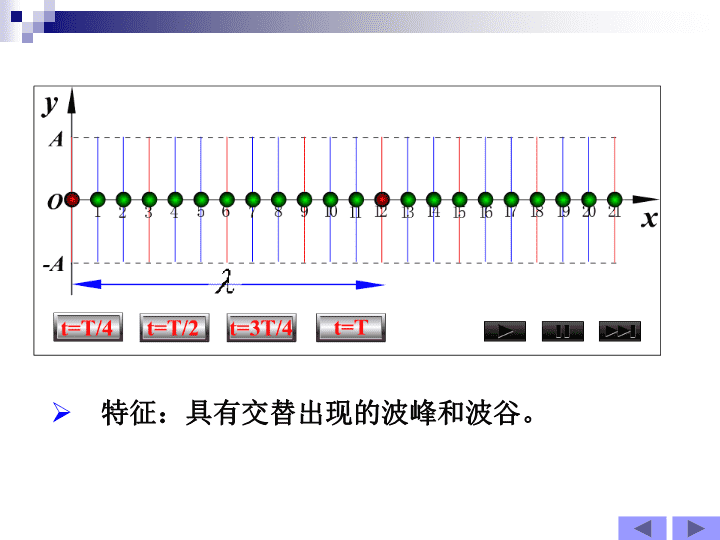
第12章机械波振动是激发波动的波源；波动是振动的传播过程。机械波：电磁波：波动机械振动在弹性介质中的传播.交变电磁场在空间的传播.两类波的不同之处机械波的传播需有传播振动的介质;电磁波的传播可以不需介质能量传播反射折射干涉衍射两类波的共同特征\n条件§12.1机械波的产生和传播一.机械波的产生波源：作机械振动的物体机械振动以一定速度在弹性介质中由近及远地传播出去，就形成机械波。弹性介质：承担传播振动的物质二.横波和纵波介质质点的振动方向与波传播方向相互垂直的波；如柔绳上传播的波。横波：\n特征：具有交替出现的波峰和波谷。\n介质质点的振动方向和波传播方向相互平行的波；如空气中传播的声波。纵波：特征：具有交替出现的密部和疏部。\n波动的特点：（1）每个质点只在平衡位置附近振动，不向前运动;（2）后面质点重复前面质点的振动状态，相位落后;（3）所有质点同一时刻位移不同，形成一个波形;（4）波动是波的振动状态、波形、能量向前传播的过程。\n三.波面和波线在波传播过程中，任一时刻媒质中振动相位相同的点联结成的面。波面：沿波的传播方向做的有方向的线。波线：波前：在某一时刻，波传播到的最前面的波面。波面平面波波线\n*球面波波前波面波线在各向同性均匀媒质中，波线⊥波面。\n四、描述波的物理量OyAA-波长：沿波的传播方向，两个相邻的、相位差为的振动质点之间的距离，即一个完整波形的长度。波长反映了波的空间周期性。\n周期：波前进一个波长的距离所需要的时间频率：周期的倒数，即单位时间内波动所传播的完整波的数目波速：波动过程中，某一振动状态（即振动相位）单位时间内所传播的距离。\n(1)波的周期和频率与媒质的性质无关；一般情况下，与波源振动的周期和频率相同。(2)波速实质上是相位传播的速度，故称为相速度；其大小主要决定于媒质的性质，与波的频率无关。说明：\n波速与介质的性质有关，为介质的密度。横波固体纵波液、气体切变模量弹性模量体积模量\n§12.2平面简谐波简谐波：介质传播的是谐振动，且波所到之处，介质中各质点作同频率的谐振动。平面简谐波：波面为平面的简谐波。本节主要讨论在无吸收（不吸收所传播的振动能量）、各向同性、均匀无限大媒质中传播的平面简谐波。简谐波是一种最简单、最基本的波，研究简谐波的波动规律是研究更复杂波的基础。\n一.平面简谐波的波函数简谐振动平面简谐波的波函数设振动方程：波从O点传播到P点所需时间：P点相位落后O点的相位:时刻\n若P为任意点：(波函数)则P点的振动方程：各质点相对平衡位置的位移波线上各质点平衡位置坐标\n波动方程的其它形式讨论:(1)由波函数可知波的传播过程中,某时刻任意两质点x1和x2振动的相位差；\nx2>x1,Δψ<0，说明x2处质点振动的相位总落后于x1处质点的振动；(2)若波沿轴负向传播时的波函数:——波程差\n例1：如图所示，为一简谐波在t=0时刻的波形图。试写出O、1、2、3点的初位相。yxt=0uO123\n解：如图画出下一时刻的波形图O123\n例2：如图所示，为一正行波在t=0时刻的波形图，已知：波速u=857m/s。由图中的参数写出此波的波动方程。y(m)x(m)t=0OA/20.1uM10\n解：由图可知：由旋转矢量法可确定波动方程为：\n二、波函数的物理意义（1）当x固定时，波函数表示该点的简谐运动方程；并给出该点与点O振动的相位差。（波具有时间的周期性）\n（波具有空间的周期性）（2）当一定时，波函数表示该时刻波线上各点相对其平衡位置的位移，即此刻的波形图。Ot时刻波形图\nOO（3）若均变化，波函数表示波形沿传播方向的运动情况（行波）。时刻时刻\n（4）波速与振动速度的区别波速：是振动状态的传播。由媒质的性质和受力状态决定。在数值上等于相速。振动速度：是波动传到的各点，在不同时刻绕自身平衡位置振动的速度。\n求：(1)波的振幅、波长、周期及波速；(2)质点振动的最大速度。例4一平面简谐波沿x轴正方向传播，已知其波函数为:标准形式:波函数为:解：比较法(与标准形式比较）\n比较可得:(2)\n振动曲线波形曲线图形研究对象物理意义特征某质点位移随时间变化规律某时刻，波线上各质点位移随位置变化规律对确定质点曲线形状一定曲线形状随t向前平移由振动曲线可知某时刻方向参看下一时刻初相周期T.振幅A由波形曲线可知该时刻各质点位移只有t=0时刻波形才能提供初相波长,振幅A某质点方向参看前一质点AyxPt0uoAytPt0To\n§12.3波的能量以绳索上传播的横波为例：波沿x方向传播，取线元是绳索的线密度OxyT2T1波动过程质元由静止开始振动质元也发生形变波动过程是能量的传播过程一.波的能量和能量密度\n线元的动能为线元的势能（原长为势能零点）为其中略去高阶项\n线元的机械能为：则：代入上式\n(1)在波的传播过程中，媒质中任一质元的动能和势能是同步变化的，即dWk=dWp，与简谐弹簧振子的振动能量变化规律是不同的；讨论:\nxyOAB(2)质元机械能随时空周期性变化，表明质元在波传播过程中不断吸收和放出能量.因此，波动过程是能量的传播过程。\n★能量密度平均能量密度设绳子的横截面为S，体密度为，则线元单位体积中的机械能（能量密度）为\n二.能流密度和波的强度单位时间内，沿波速方向，垂直通过单位面积的能量称能流密度。su△t\n波的强度：一个周期内能流密度大小的平均值。三.波的吸收为介质吸收系数，与介质的性质、温度、及波的频率有关。\n瑞典皇家科学院4日宣布，美国和澳大利亚的三名物理学家因超新星的研究获得2011年诺贝尔物理学奖布莱恩-施密特索尔-帕尔马特亚当-黎斯\n\n§12.4惠更斯原理波的衍射水波通过狭缝后的衍射波的衍射:波在传播过程中遇到障碍物时，能绕过障碍物的边缘，在障碍物的阴影区内继续传播的现象。\n惠更斯提出：(1)行进中的波面上任意一点都可看作是新的子波源；(3)各个子波所形成的包络面，就是原波面在一定时间内所传播到的新波面。(2)所有子波源各自向外发出许多子波；\n球面波O\n(1)知某一时刻波前，可用几何方法决定下一时刻波前；说明：(2)亦适用于电磁波，非均匀和各向异性媒质；(3)解释衍射、反射、折射现象；(4)不足之处（未涉及振幅，相位等的分布规律）。\n§12.5波的干涉一.叠加原理1.波传播的独立性\n2.波的叠加原理在波相遇区域内，任一质点的振动，为各波单独存在时所引起的振动的合振动。当几列波在传播过程中在某一区域相遇后再行分开，各波的传播情况与未相遇一样，仍保持它们各自的频率、波长、振动方向等特性继续沿原来的传播方向前进。\n\n二.相干波与相干条件相干条件：频率相同、振动方向相同、相位差恒定。当两列（或多列）相干波叠加的结果，其合振幅A和合强度I将在空间形成一种稳定的分布，即某些点上的振动始终加强，某些点上的振动始终减弱。——波的干涉相干波：满足相干条件的波相干波源：产生相干波的波源\n三.干涉规律*波源振动方程：点P的两个分振动：\n*点P的两个分振动常量\n讨论其他振动始终加强振动始终减弱\n波程差若则振动始终减弱振动始终加强其他\n★从能量上看，当两相干波相遇时，在两波交叠的区域，合成波在空间各处的强度并不等于两个分波强度之和，而是发生重新分布。这种新的强度分布是时间上稳定的、空间上强弱相间具有周期性的一种分布。\n例：A、B为两相干波源，距离为10m，振幅相同，相同，初相差为,u=400m/s,f=100Hz。求：A、B连线上因干涉而静止的各点位置。P10mr1r2BA解：（P在B左侧）（P在A右侧）(即在两侧干涉相长，不会出现静止点)P点在A，B两侧\nBAP10mr1r2P在A、B中间在A，B之间距离A点为r1=1,3,5,7,9m处出现静止点。干涉相消\n§13.6驻波一驻波的产生振幅和波速都相同的两列相干波，在同一直线上沿相反方向传播时叠加而形成的一种特殊的干涉现象.uu\n二.驻波方程驻波的振幅与位置有关正向负向各质点都在作同频率的简谐运动（驻波方程）\n驻波方程讨论10(1)振幅随x而异，与时间无关.波腹波节\n相邻两波腹之间的距离：相邻两波节之间的距离：(2)所有波节点将媒质划分为长的许多段，每段中各质点的振动振幅不同，但相位皆相同；而相邻段间各质点的振动相位相反;即驻波中不存在相位的传播。\n三.驻波的能量驻波的能量在相邻的波腹和波节间往复变化，在相邻的波节间发生动能和势能间的转换，动能主要集中在波腹，势能主要集中在波节，但无长距离的能量传播。ABC波节波腹位移最大时平衡位置时\n四.相位跃变（半波损失）反射点为波节有半波损失（波节）（相当于入射波与反射波之间附加了半个波长的波程差）无半波损失（波腹）◆透射波没有半波损失！入射波反射波透射波\n五.弦线上的驻波实验(a)(b)(c)AAABBBC1C2C3C1C2D1D4D2D3D1D2D3波腹：D1,D2,D3,D4波节：C1,C2,C3驻波条件：\n六.振动的简正模式\n弦线上形成驻波的条件：驻波频率则为：由此频率决定的各种振动方式称为弦线振动的简正模式。\n例：一沿x轴正方向传播的入射波的波函数，在x=0处发生反射，反射点为一节点。求：（1）反射波的波函数；（2）驻波的波函数；（3）驻波的波腹和波节的位置坐标。\n(3)以B为反射点求合成波，并分析波节，波腹的位置坐标。求：(1)以D为原点，写出波函数；例：平面简谐波t时刻的波形如图，此波波速为u，沿x方向传播，振幅为A，频率为f。(2)以B为反射点，且为波节，若以B为x轴坐标原点，写出入射波，反射波方程；\n§13.7多普勒效应由于观察者（接收器）或波源、或二者同时相对媒质运动，而使观察者接收到的频率与波源发出的频率不同的现象，称为多普勒效应。是波源的频率。即：单位时间内波源振动的次数或发出的‘完整波’的个数；是观察者接受到的频率。即：观察者在单位时间内接受到的完整的波数。规定：表示观察者相对于媒质的运动速度。表示波源相对于媒质的运动速度。\n一.波源不动，观察者相对介质以速度运动观察者接收的频率观察者向波源运动观察者远离波源\n二.观察者不动，波源相对介质以速度运动观察者A\n三.波源与观察者同时相对介质运动观察者向波源运动+，远离.波源向观察者运动，远离+.当时，所有波前将聚集在一个圆锥面上，波的能量高度集中形成冲击波或激波，如核爆炸、超音速飞行等.\n5）卫星跟踪系统等.1）交通上测量车速；2）医学上用于测量肿瘤；3）天文学家利用电磁波红移说明大爆炸理论；4）用于贵重物品、机密室的防盗系统；多普勒效应的应用\n电磁波如光波，也有多普勒效应，光与接收器的相对速度决定接收器接收的频率。可以用相对论(相对性原理和光速不变原理)证明：当光源和接收器在同一直线上运动时,其速度为观察者所接收到的频率为：c为真空中的光速当光源远离接收器时，接收到的频率变小，因而波长变长，这种现象叫做“红移”。如来自星球与地面同一元素的光谱比较，发现几乎都发生红移。这就是“大爆炸”宇宙学理论的重要依据。\n本章小结：1、机械波及表述波的物理量2、平面简谐波的波动方程及物理意义\n3、波的能量4、惠更斯原理波的叠加原理5、波的干涉及其规律6、驻波及驻波方程\n7、多普勒效应