物理答案(大学物理) 11页

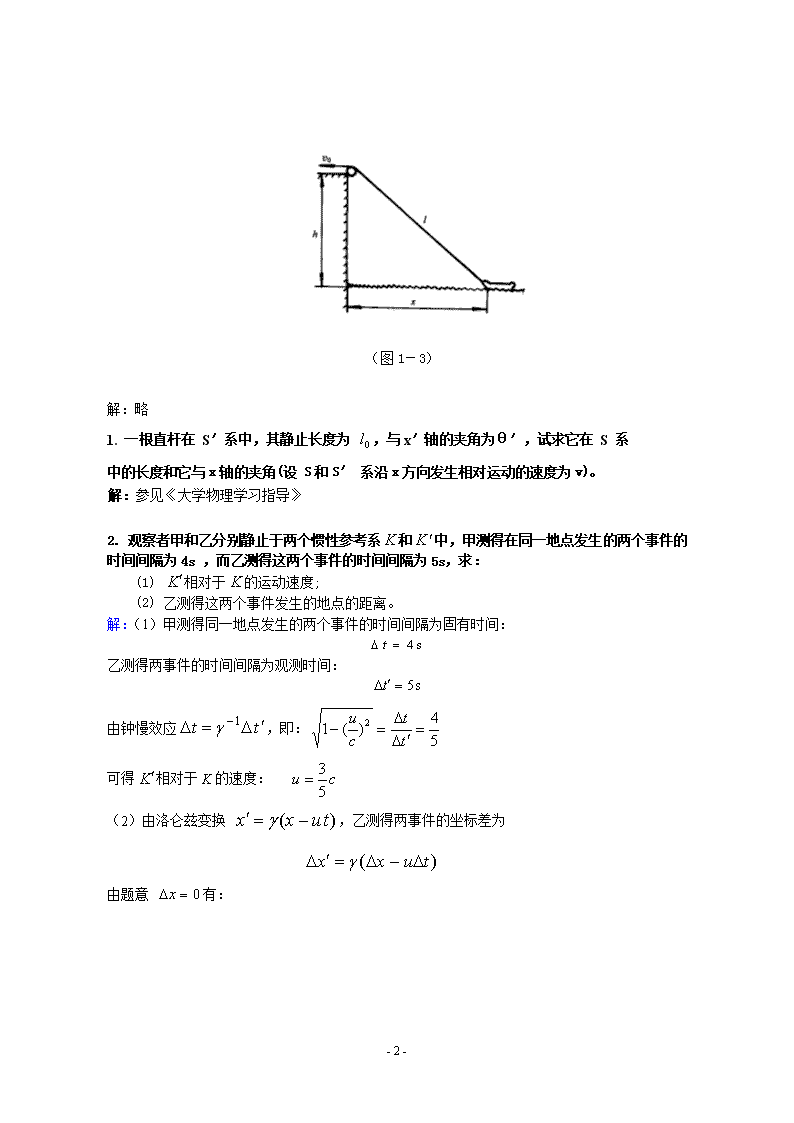
1.一个人自原点出发，25s内向东走30m，又10s内向南走10m，再15s内向正西北走18m。求在这50s内，(1)平均速度的大小和方向;(2)平均速率的大小。（图1－2）解：建立如图坐标系。（1）50s内人的位移为则50s内平均速度的大小为：方向为与x轴的正向夹角：（2）50s内人走的路程为S=30+10+18=58(m)，所以平均速率为2.如图1－3所示，在离水面高为h的岸上，有人用绳拉船靠岸，船在离岸边x处。当人以v的速率收绳时，试问船的速度、加速度的大小是多少?并说明小船作什么运动。-11-\n（图1－3）解：略1.一根直杆在S′系中，其静止长度为，与x′轴的夹角为θ′，试求它在S系中的长度和它与x轴的夹角(设S和S′系沿x方向发生相对运动的速度为v)。解：参见《大学物理学习指导》2.观察者甲和乙分别静止于两个惯性参考系和中，甲测得在同一地点发生的两个事件的时间间隔为4s，而乙测得这两个事件的时间间隔为5s，求：(1)相对于的运动速度;(2)乙测得这两个事件发生的地点的距离。解：（1）甲测得同一地点发生的两个事件的时间间隔为固有时间：乙测得两事件的时间间隔为观测时间：由钟慢效应，即：可得相对于K的速度：（2）由洛仑兹变换，乙测得两事件的坐标差为由题意有：-11-\n即两事件的距离为3.一电子以0.99c(c为真空中光速)的速率运动。试求：(1)电子的总能量是多少？(2)电子的经典力学动能与相对论动能之比是多少？(电子静止质量)解：(1)由相对论质能公式，电子的总能量为(2)电子的经典力学动能为，相对论动能为，二者之比为4.设快速运动介子的能量约为，而这种介子在静止时的能量为。若这种介子的固有寿命是，求它运动的距离(真空中光速度)。解：先求出快速运动介子的运动速度，这个寿命乘以即可。-11-\n三计算题1.飞机降落时的着地速度大小，方向与地面平行，飞机与地面间的摩擦系数，迎面空气阻力为，升力为(是飞机在跑道上的滑行速度，和均为常数)。已知飞机的升阻比K=/=5，求飞机从着地到停止这段时间所滑行的距离。(设飞机刚着地时对地面无压力)解：以飞机着地处为坐标原点，飞机滑行方向为x轴，竖直向上为y轴，建立直角坐标系。飞机在任一时刻（滑行过程中）受力如图所示，其中为摩擦力，为空气阻力，为升力。由牛顿运动定律列方程：（1）（2）由以上两式可得分离变量积分：得飞机坐标x与速度v的关系令v=0，得飞机从着地到静止滑行距离为根据题设条件，飞机刚着地时对地面无压力，即-11-\n得所以有2.一颗子弹由枪口射出时的速率为v，子弹在枪筒内被加速时，它所受到的合力(a,b为常量)。解：参见《大学物理学习指导》。三计算题１．一半径为R的圆形平板放在水平桌面上，平板与水平桌面的摩擦系数为u，若平板绕通过其中心且垂直板面的固定轴以角速度开始旋转，它将在旋转几圈后停止？解：设圆板面密度为，则转动时受到的摩擦阻力矩大小为由转动定律可得角加速度大小设圆板转过n转后停止，则转过的角度为。由运动学关系可得旋转圈数2．如图所示，两物体的质量分别为和，滑轮的转动惯量为J，半径为r。(1)若与桌面的摩擦系数为μ，求系统的加速度a及绳子中的张力(绳子与滑轮间无相对滑动)；-11-\n(2)若与桌面为光滑接触，求系统的加速度a及绳子中的张力。解：参见《大学物理学习指导》3．半径为R具有光滑轴的定滑轮边缘绕一细绳，绳的下端挂一质量为m的物体，绳的质量可以忽略，绳与定滑轮之间无相对滑动，若物体下落的加速度为a，求定滑轮对轴的转动惯量。解：分别以定滑轮和物体为研究对象，对物体应用牛顿运动定律，对定滑轮应用转动定律列方程：（1）（2）由牛顿第三定律有（3）由角量和线量的关系有（4）由以上四式联解可得三　计算题1．一长为l，质量为m的匀质链条，放在光滑的桌面上，若其长度的1/5悬挂于桌边下，将其慢慢拉回桌面，外力需做功为多少?-11-\n解：设桌面为重力势能零势面，以向下为坐标轴正向。在下垂的链条上坐标为处取质量元，将它提上桌面，外力反抗重力作功，将悬挂部分全部拉到桌面上，外力作功为：2．一质量为m的质点，仅受到力的作用，式中k为常数，为从某一定点到质点的矢径。该质点在处由静止开始运动，则当它到达无穷远时的速率为多少?。解：因质点受力是有心力，作功与路径无关，故由动能定理有：质点到达无穷远时的速率：3．一人从10m深的井中提水，起始时桶中装有10kg的水，桶的质量为1kg，由于水桶漏水，每升高1m要漏去0.2kg的水。求水桶匀速地从井中提到井口，人所作的功。解：如图所示，以井中水面为坐标原点，以竖直向上为轴正方向。因为匀速提水，所以人的拉力大小等于水桶和水的重量，它随升高的位置变化而变化，在高为y处，拉力为式中，。人作功为-11-\n三计算题1.一超声波源发射声波的功率为10W。假设它工作10s，并且全部波动能量都被1mol氧气吸收而用于增加其内能，问氧气的温度升高了多少？（氧气分子视为刚性分子，摩尔气体常量R＝8.31(J·mol·K)）解：，式中P为功率，则2.计算下列一组粒子的平均速率和方均根速率:粒子数N24682速率v(m×s-1)10.020.030.040.050.0解：平均速率为最概然速率方均根速率为3．储有氧气的容器以100m·s的速度运动。假设该容器突然停止，全部定向运动的动能都变为气体分子热运动的动能，问容器中氧气的温度将会上升多少?解：参见《大学物理学习指导》。-11-\n三　计算题1．一定量的理想气体，经如图所示的过程由状态a变为状态c(ac为一直线)，求此过程中(1)气体对外做的功；(2)气体内能的增量；(3)气体吸收的热量。解：参见《大学物理学习指导》２．0.02kg的氦气(视为理想气体)，温度由17℃升为27℃．若在升温过程中，(1)体积保持不变；(2)压强保持不变；(3)不与外界交换热量；试分别求出气体内能的改变、吸收的热量、外界对气体所作的功．(普适气体常量R=8.31)解：氦气为单原子分子理想气体，(1)等体过程，V＝常量，W=0据Q＝DE+W可知＝623J3分(2)定压过程，p=常量，=1.04×103JDE与(1)相同．W=Q-DE＝417J4分(3)Q=0，DE与(1)同-11-\nW=-DE=-623J(负号表示外界作功)3分三计算题（循环过程，选做）１．一致冷机用理想气体为工作物质进行如图所示的循环过程，其中ab、cd分别是温度为T2、T1的等温过程，bc、da为等压过程．试求该致冷机的致冷系数．解：在ab过程中，外界作功为在bc过程中，外界作功在cd过程中从低温热源T1吸取的热量等于气体对外界作的功，其值为在da过程中气体对外界作的功为致冷系数为2.已知一定量的理想气体经历如图所示的循环过程。其中ab和cd是等压过程，bc和da是绝热过程。已知b点温度，c点温度。证明该热机的效率为证：等压过程吸热-11-\n　　等压过程放热所以(1)与求证结果比较，只需证得即可，为此，列出ab,cd的等压过程方程和bc,da绝热过程方程：(2)(3)(4)(5)联立上述四式，可得，代入(1)式得证-11-