大学物理C课后答案 15页

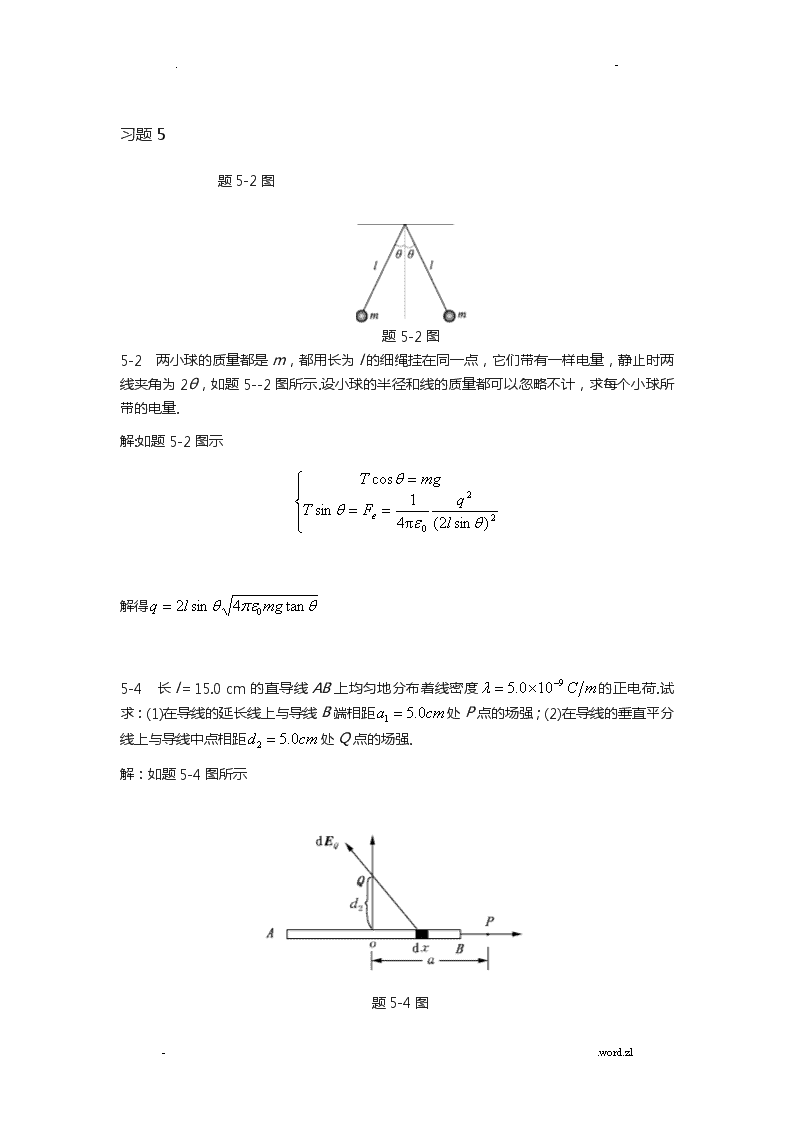
.-习题5题5-2图题5-2图5-2　两小球的质量都是m，都用长为l的细绳挂在同一点，它们带有一样电量，静止时两线夹角为2θ，如题5--2图所示.设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量.解:如题5-2图示解得5-4　长l＝15.0cm的直导线AB上均匀地分布着线密度的正电荷.试求：(1)在导线的延长线上与导线B端相距处P点的场强；(2)在导线的垂直平分线上与导线中点相距处Q点的场强.解：如题5-4图所示题5-4图-.word.zl\n.-(1)在带电直线上取线元，其上电量在点产生场强为用，,代入得方向水平向右(2)同理方向如题5-4图所示由于对称性，即只有分量，∵以,,代入得，方向沿轴正向5-7　半径为和()的两无限长同轴圆柱面，单位长度上分别带有电量λ和－λ，试求：(1)；(2)；(3)处各点的场强.解:高斯定理-.word.zl\n.-取同轴圆柱形高斯面，侧面积那么对(1)(2)∴沿径向向外(3)∴5-9　如题5-9图所示，在A，B两点处放有电量分别为＋q，－q的点电荷，AB间距离为2R，现将另一正试验点电荷从O点经过半圆弧移到C点，求移动过程中电场力做的功.解:如题5-9图示∴题5-9图　　　　　　　　　　　　　题5-10图5-10　如题5-10图所示的绝缘细线上均匀分布着线密度为λ的正电荷，两段直导线的长度和半圆环的半径都等于R.试求环中心O点处的场强和电势.解:(1)由于电荷均匀分布与对称性，和段电荷在点产生的场强互相抵消，取那么产生点如图，由于对称性，点场强沿轴负方向-.word.zl\n.-题5-10图［］(2)电荷在点产生电势，以同理产生半圆环产生∴习题66-5　在真空中，有两根互相平行的无限长直导线L1和L2，相距0.10m，通有方向相反的电流，，，如题6-5图所示.A，B两点与导线在同一平面.这两点与导线L2的距离均为5.0cm.试求A，B两点处的磁感应强度，以及磁感应强度为零的点的位置.-.word.zl\n.-题6-5图解：如题6-5图所示,方向垂直纸面向里(2)设在外侧距离为处那么解得6-7　设题6-7图中两导线中的电流均为8A，对图示的三条闭合曲线a，b，c，分别写出安培环路定理等式右边电流的代数和.并讨论：(1)在各条闭合曲线上，各点的磁感应强度的大小是否相等？(2)在闭合曲线c上各点的是否为零？为什么？题6-7图解：(1)在各条闭合曲线上，各点的大小不相等．(2)在闭合曲线上各点不为零．只是的环路积分为零而非每点．-.word.zl\n.-题6-10图6-10　如题6-10图所示，在长直导线AB通以电流，在矩形线圈CDEF有电流，AB与线圈共面，且CD，EF都与AB平行.a＝9.0cm，b＝20.0cm，d＝1.0cm，求：(1)导线AB的磁场对矩形线圈每边所作用的力；(2)矩形线圈所受合力和合力矩.解：(1)方向垂直向左，大小同理方向垂直向右，大小方向垂直向上，大小为方向垂直向下，大小为(2)合力方向向左，大小为合力矩∵线圈与导线共面∴．-.word.zl\n.-题6-12图6-12　一长直导线通有电流，旁边放一导线ab，其有电流，且两者共面，如题6-12图所示.求导线ab所受作用力对O点的力矩.解：在上取，它受力向上，大小为对点力矩方向垂直纸面向外，大小为题6-13图6-13　电子在的匀强磁场中作圆周运动，圆周半径r＝3.0cm.垂直于纸面向外，某时刻电子在A点，速度v向上，如题6-13图所示.(1)试画出这电子运动的轨道；(2)求这电子速度v的大小；(3)求这电子的动能.解：(1)轨迹如图题6-13图(2)∵∴-.word.zl\n.-(3)习题77-1　一半径r＝10cm的圆形回路放在B＝0.8T的均匀磁场中，回路平面与B垂直.当回路半径以恒定速率cm/s收缩时，求回路中感应电动势的大小.解:回路磁通感应电动势大小题7-37-3　如题7-3图所示，在两平行载流的无限长直导线的平面有一矩形线圈.两导线中的电流方向相反、大小相等，且电流以的变化率增大，求：(1)任一时刻线圈所通过的磁通量；(2)线圈中的感应电动势.解:以向外磁通为正那么(1)(2)习题88-1　质量为10×10－3kg的小球与轻弹簧组成的系统，按(SI)的规律做谐振动，求：-.word.zl\n.-(1)振动的周期、振幅、初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等？(3)t2＝5s与t1＝1s两个时刻的位相差.解：(1)设谐振动的标准方程为，那么知：又(2)当时，有，即∴(3)8-2　一个沿x轴做简谐振动的弹簧振子，振幅为A，周期为T，其振动方程用余弦函数表出.如果t＝0时质点的状态分别是：(1)x0＝－A；(2)过平衡位置向正向运动；(3)过处向负向运动；(4)过处向正向运动.试求出相应的初位相，并写出振动方程.解：因为将以上初值条件代入上式，使两式同时成立之值即为该条件下的初位相．故有-.word.zl\n.-8-3　一质量为10×10－3kg的物体做谐振动，振幅为24cm，周期为4.0s，当t＝0时位移为＋24cm.求：(1)t＝0.5s时，物体所在的位置及此时所受力的大小和方向；(2)由起始位置运动到x＝12cm处所需的最短时间；(3)在x＝12cm处物体的总能量.解：由题∴又，时，故振动方程为(1)将代入得方向指向坐标原点，即沿轴负向．(2)由题知，时，，时∴(3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为-.word.zl\n.-8-5　题8-5图为两个谐振动的x－t曲线，试分别写出其谐振动方程.题8-5图解：由题8-5图(a)，∵时，即故由题8-5图(b)∵时，时，又∴故习题9机械波9-4　波源在原点的一列平面简谐波，波动方程为y＝Acos(Bt－Cx)，其中A，B，C为正值恒量.求：(1)波的振幅、波速、频率、周期与波长；(2)写出传播方向上距离波源为l处一点的振动方程；(3)任一时刻，在波的传播方向上相距为d的两点的位相差.-.word.zl\n.-解:(1)平面简谐波的波动方程()将上式与波动方程的标准形式比较，可知：波振幅为，频率，波长，波速，波动周期．(2)将代入波动方程即可得到该点的振动方程(3)因任一时刻同一波线上两点之间的位相差为将，及代入上式，即得．9-5　沿绳子传播的平面简谐波的波动方程为y＝0.05cos(10πt－4πx)，式中x，y以m计，t以s计.求：(1)波的波速、频率和波长；(2)绳子上各质点振动时的最大速度和最大加速度；(3)求x＝0.2m处质点在t＝1s时的位相，它是原点在哪一时刻的位相？这一位相所代表的运动状态在t＝1.25s时刻到达哪一点？解:(1)将题给方程与标准式相比，得振幅，频率，波长，波速．-.word.zl\n.-(2)绳上各点的最大振速，最大加速度分别为(3)m处的振动比原点落后的时间为故,时的位相就是原点()，在时的位相，即π．设这一位相所代表的运动状态在s时刻到达点，那么9-7　如题9-7图所示，S1和S2为两相干波源，振幅均为A1，相距，S1较S2位相超前，求：题9-7图(1)S1外侧各点的合振幅和强度；(2)S2外侧各点的合振幅和强度.解：〔1〕在外侧，距离为的点，传到该点引起的位相差为〔2〕在外侧.距离为的点，传到该点引起的位相差.9-9　一驻波方程为y＝0.02cos20xcos750t(SI)，求：(1)形成此驻波的两列行波的振幅和波速；(2)相邻两波节间距离.-.word.zl\n.-解:(1)取驻波方程为故知，那么，∴(2)∵所以相邻两波节间距离习题10波动光学10-4　在氏双缝实验中，双缝间距d＝0.20mm，缝屏间距D＝1.0m.试求：(1)假设第2级明条纹离屏中心的距离为6.0mm，计算此单色光的波长；(2)求相邻两明条纹间的距离.解:(1)由知，，∴(2)10-5　在双缝装置中，用一很薄的云母片(n＝1.58)覆盖其中的一条缝，结果使屏幕上的第7级明条纹恰好移到屏幕中央原零级明纹的位置.假设入射光的波长为550nm，求此云母片的厚度.解:设云母片厚度为，那么由云母片引起的光程差为按题意∴-.word.zl\n.-10-7　在折射率n1＝1.52的镜头外表涂有一层折射率n2＝1.38的MgF2增透膜，如果此膜适用于波长λ＝550nm的光，问膜的厚度应取何值？解:设光垂直入射增透膜，欲透射增强，那么膜上、下两外表反射光应满足干预相消条件，即∴令，得膜的最薄厚度为．当为其他整数倍时，也都满足要求．教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。-.word.zl