大学物理 磁力课件 36页

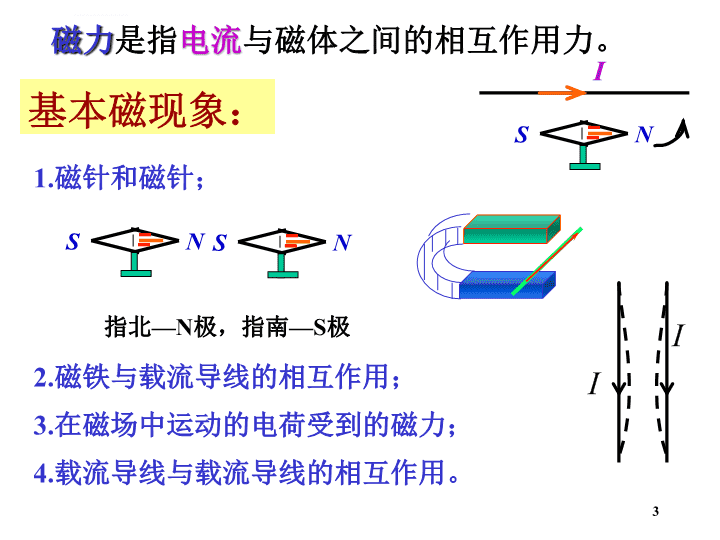
本节主要内容：2.1磁力与电荷的运动2.2磁场与磁感应强度2.3带电粒子在磁场中的运动2.4霍尔效应2.5载流导线在磁场中受的力本节学习要点1.磁感应强度2.磁力线和磁通量1\n2.1磁力与电荷的运动2\n1.磁针和磁针；4.载流导线与载流导线的相互作用。3.在磁场中运动的电荷受到的磁力；2.磁铁与载流导线的相互作用；INSNSNS磁力是指电流与磁体之间的相互作用力。基本磁现象：指北—N极，指南—S极3\n磁力是运动电荷之间的相互作用.一切磁现象的根源是电流.结论永磁体也是由分子原子组成的，在分子内部，电子和质子等带电粒子的运动也形成微小的电流，叫分子电流。永磁体是分子电流方向定向排列。永磁体与其他永磁体或电流的相互作用，实际上是整齐排列的分子电流之间或他们与导线中定向运动的电荷之间的相互作用。4\n用磁感应强度描述磁场强弱的一个物理量.2.2磁场与磁感应强度运动电荷磁场运动电荷磁场：磁极或电流在自己周围的空间产生一个磁场磁场的基本性质之一是他对于任何置于其中的其他磁极或电流施加作用力磁力作用方式5\n(2)磁作用力F还与粒子的运动方向有关,在一定的方向时F最大为Fm.(1)在磁场中某点运动的电荷,所受磁作用力,与电荷量q,速度的大小v成正比.的方向定义如图定义B的大小为B=Fm/qvB的单位:特斯拉(T)地磁场B大约10-4T一、磁力(洛伦兹力)注意：磁感应强度是描述磁场本身性质的量，与电荷无关。6\n在磁场中运动的带电粒子受磁场力--洛仑兹力：大小:F=qvBsin方向如图,垂直于v、B构成的平面.+q-q(显然当=0时F=0)二磁感应强度的叠加原理（磁场源）7\n磁感应线，I磁感应线是无头无尾的闭合曲线NS线三磁感应线与磁通量8\n(1)磁感应线是环绕电流的闭合曲线，无始无终;(2)任何两条磁感应线在空间不会相交;(4)磁感应线的方向与电流的流向遵守右手螺旋法则。(3)磁感应线的疏密表示磁感应强度的大小，切线方向表示磁感应强度的方向；磁力线性质I9\nm=BSSS磁通量单位：韦伯标量＝磁力线的总条数10\n穿过闭合曲面的磁通量规定外法线方向为正磁力线穿出闭合面磁力线穿入闭合面BBnn为正通量。为负通量。11\n磁场中的高斯定理由于磁力线为闭合曲线，穿入穿出闭合面的磁力线根数相同，正负通量抵消。穿过闭合面的磁通量等于零。12\n磁场中的高斯定理阐明了磁场的性质：磁场是无源场，磁力线为闭合曲线，磁场是涡旋场.磁场与电场有本质的区别，电场是有源场,电力线是发散的。电场是发散场。13\n1.磁感应强度：2.磁力线的性质3.磁通量标量4.磁场中的高斯定律小结大小：B=Fm/qv的方向定义如图洛仑兹力：14\n1.导体中形成电流的条件：在导体内有可以自由移动的电荷或叫载流子在导体两端要存在有电势差2.电流密度矢量:3.电源电动势4.欧姆定律的微分形式回顾15\n1.磁感应强度：2.磁力线的性质3.磁通量标量4.磁场中的高斯定律回顾大小：B=Fm/qv的方向定义如图洛仑兹力：16\n(1)粒子平行于磁场运动+qq-q+q-RR(2)粒子垂直于均匀磁场运动F=0,匀速直线运动.+qq-圆周轨道半径:运动一周的时间:2.3带电粒子在磁场中的运动17\n(3)粒子以一定角度进入均匀磁场+qh将速度分解为：v//=sin,v=cos(4)粒子以一定角度进入非均匀磁场磁约束18\n带电粒子在电场和磁场中运动受力：若无其它外力则有：于是原则上可解出粒子的运动情况.带电粒子在电场和磁中运动的应用19\n-eFPUII~主要原理:带电粒子在均匀磁场的运动周期:与粒子的速度无关.应用:显象管内的电子磁聚焦,实验室测量粒子比荷q/m.一磁聚焦电子束：小发散角，磁场方向速度基本相同，螺距相同hB螺距相同20\n回旋加速器结构示意如图:在半圆形盒子中的运动时间粒子引出时的速度:NS接震荡器D2D1D2D1震荡器粒子束分析被加速粒子的电荷正负.粒子运动的轨道半径:引出时的能量:二回旋加速器21\n实际上必须计入相对论效应,即:因此为保证同步加速,震荡器的频率要满足下式在半圆形盒子中的运动时间:22\n用途:测量粒子的m、q及q/m（荷质比）等物理量.速度选择器应用例:用铅同位素含量比例测量古生物年龄.最简单的质谱仪如图:根据:+qRN'A狭缝1狭缝2++++----+-速度选择器工作原理:得:三质谱仪23\n现象,霍尔效应,霍尔电势差.V+++++---------------+V+++++------++++++++++实验表明:-qv-+qv+IbdIbdRH称为霍尔系数.理论推导:平衡时电流:2.4霍尔效应24\n讨论1.由于导体内有大量的自由电荷，n较大，RH较小，故导体的霍尔效应较弱。2.半导体界于导体与绝缘体之间，其内的自由电荷较少，n较小，RH较大，故半导体的霍尔效应显著。25\n霍尔效应的应用:测量磁感应强度、电流，半导体类型判别等.磁流体发电的构想:等离子体流通过磁场,其中的正负电荷向相反方向运动.-qv-+qv++-SN发电通道导电气体26\n实验表明,载流导线在磁场受力I-q+q2.5载流导线在磁场受的力安培力电流元：导线截面积S，电流I，长度dl.电流元的方向：规定为电流方向安培力：载流导线受磁场的作用力27\n导线中的电流是由其中的载流子定向移动形成的，当把载流导线置于磁场中时，这些运动的载流子受到洛伦兹力作用安培力的产生原因:实际计算中,用力的分量式积分.I-q+q一段载流导线L在磁场受力:注意：载流导体受到的安培力是大量运动电荷受到的洛仑兹力的宏观表现。I其中28\n例：载流导线（R，I）在磁场B中所受到的力？x0y解：由对称性分析你能得到什么结论？方向：+y29\n载流线圈在磁场中如图：Il1.受力：力矩：力矩矢量：其中线圈的磁矩：一般式：适用于在均匀磁场中任何形状的线圈.l1l2磁场对载流线圈的作用磁矩面方向与电流的流向符合右手螺旋关系30\n试分析下述情况：.II..I总结载流线圈在磁场中运动的规律：….=0,M=0=,M=0作用在线圈上的磁力与力矩均不为零：载流线圈在非均匀磁场中：,M=Mmax31\n例：求M？向里xyIrR解：1.微元迭加法注意：各电流元产生的力矩元的方向相同。方向：+y2.由32\n圆周轨道半径:运动一周的时间:带电粒子在磁场中的运动1.洛伦兹力小结33\n带电粒子在电场和磁场中运动受力：若无其它外力则有：原则上可解出粒子的运动情况.2.霍尔效应霍尔系数霍尔电势差34\n载流导线在磁场受力3.载流导线在磁场受的力安培力电流元的方向：规定电流方向用力的分量式积分.一段载流导线L在磁场受力:I35\n载流线圈在磁场中的力矩矢量其中线圈的磁矩：一般式：适用于在均匀磁场中任何形状的线圈.4.磁场对载流线圈的作用磁矩面方向与电流的流向符合右手螺旋关系36