- 12.64 MB
- 2022-08-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
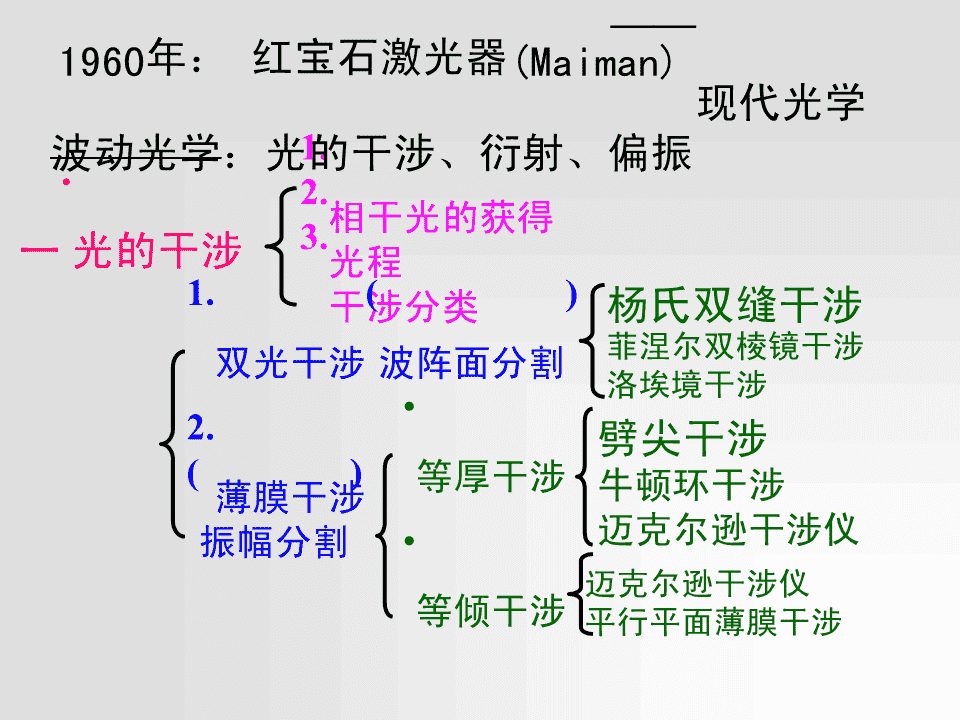
18光学简史17世纪�粒子说(Newton)波动说(Huygens)19世纪�双缝实验(ThomasYoung)电磁理论(Maxwell)——光的波动性20世纪初�光电效应康普顿效应(Compton)——光的波粒二象性\n1960年�红宝石激光器(Maiman)——现代光学波动光学�光的干涉、衍射、偏振1.相干光的获得一.光的干涉2.光程3.干涉分类杨氏双缝干涉菲涅尔双棱镜干涉1.双光干涉(波阵面分割)洛埃境干涉劈尖干涉2.薄膜干涉•等厚干涉牛顿环干涉(振幅分割)迈克尔逊干涉仪迈克尔逊干涉仪•等倾干涉平行平面薄膜干涉\n二.光的衍射1.菲涅尔衍射(近场)•夫琅和费单缝衍射2.夫琅和费衍射(远场)•夫琅和费圆孔衍射•光栅衍射•x射线衍射三.光的偏振1.自然光和光的偏振现象2.偏振光的获得3.偏振光的检测\n第一节光的干涉一.相干光的获得1.相干条件�频率相同、振动方向、相位差恒定2.相干光源:能级跃迁辐射波列E2�=(E2-E1)/hE1波列长L=�c·独立·(不同原子发的光)独立(同一原子先后发的光)\n•不同原子发出的光�一般不是相干光。•同一原子发出的一束光,分成两束后成为相干光。分波面法分振幅法p·pS*S*薄膜薄膜*激光光源�E2��完全一样�=(E2-E1)/h�(频率,位相,振动方向,传播方向)E1\n3.干涉分类•双光干涉(波阵面分割)•杨氏双缝干涉•菲涅尔双棱镜干涉•洛埃境干涉•薄膜干涉(振幅分割)劈尖干涉•等厚干涉牛顿环干涉迈克尔逊干涉仪•等倾干涉迈克尔逊干涉仪平行平面薄膜干涉\np4.两列光波的叠加r1·方向,频率相同1E�Ecos(�t��)·r211010·E0E�Ecos(�t��)E20220202222E�E�E�2EEcos��010201020�0��E10I�I�I�2IIcos��20101212�非相干光源:cos���0,I�I1�I2--非相干叠加�相干光源cos���cos���I�I�I�2II,����2k�--干涉相长(明)�max1212I����Imin�I1�I2�2I1I2,����(2k�1)�-干涉相消(暗)\n二.光程�r•真空中:���2�aλb··�真空r2-r1•媒质中:�rn�rn���2��2�aλnb��··媒质真空r-r21媒质1.光程定义:L=nd�n1n2……nm……d1d2dm\n2.光程的物理意义:•光在介质中几何路程d�与在真空中几何路程nd所经历的相位变化相同。•光程本质�把介质中路程折合成真空中路程3.光程差:�=L2-L1�•相位差和光程差的关系����2��真空����k�����2k�--干涉相长(明)真空���2k�1����(2k�1)�-干涉相消(暗)�����真空�2\n例1.2������L�L21�r·p12�S1n�r�d�nd�rr212�Sd22��r�r�n�1d21�例2.在真空中波长为�的单色光,在折射率为n的透明介质中从A沿某路径传播到B,若A、B两点位相差为3��则此路径AB的光程为(A)1.5�(B)1.5n�(C)3�(D)1.5�/n[A]\nP2.使用透镜不会产生附加光程差S1�L�S2QS2QS123.反射光的相位突变和附加光程差n1nA··C•光疏→光密,反射光有半波损失.2·nB31.n1�n2�n3,n1�n2�n3•光密→光疏,1,2都没有,�无半波损失.•光疏→光密�1,2都有��无半波损失.2.n1�n2�n3,n1�n2�n3�有半波损失.\n.1.杨氏双缝干涉1801年,ThomasYoung(1773-1829)单色光入射pxxr1·x�x��r2dox0I�DD>>d>>λ(D�m,d�10-4m,λ�10-7m)①光程差�rrx21�dsin��dtg��d�D\npxxr1·xr�x�2dox0I�DD明纹位置:���k�,x�k��k�,k�0,1,2…d�D暗纹位置:���(2k�1),x��(2k�1)��(2k�1)22d②条纹特点�D�x���一系列平行的明暗相间的条纹�d��不太大时条纹等间距�例.上缝加介质膜?�中间级次低�例.复光照射?\n2.在双缝干涉实验中�为使屏上的干涉条纹间距变大�可以采取的办法是�D�A�使屏靠近双缝�x�B�使两缝的间距变小�d�C�把两个缝的宽度稍微调窄��D�改用波长较小的单色光源。[B]\n3.在双缝干涉实验中�双缝间距为2mm�双缝与屏的间距为300cm�入射光的波长为600nm�在屏上形成的干涉图样的明纹间距为(1nm=10-9m)。�A�4.5nm��B�0.9mm�[B]�C�3.1nm��D�1.2nm。\n4.在图示的双缝干涉实验中�若用玻璃片折射率n1=1.4覆盖缝S�用折射率n�1.7覆盖缝S�将使122屏上原来未放玻璃时的中央明条纹所在处o变为第五条明纹�设单色光波长�=480nm�求玻璃片的厚度d�可认为光线垂直穿过玻璃片�.d解�原来��r�r�012覆盖玻璃后�nS1r11��(r�nd�d)�(r�nd�d)2211do�5�(n2n1)d5S2r2n25�d��8.0�10�6mn�n21\n�光强公式I4I0-4�-2�02�4���-2-1012kx-2x-10x1x2x-2�/d-�/d0�/d2�/dsin�III2IIcos1212dsin�2���2�I4Icos�022.菲涅尔双棱镜实验3.洛埃镜实验\n五.薄膜干涉�一�--等倾条纹r环oP*1.薄膜干涉条纹iif光束1、2的光程差�1L�S·2��n(AB�BC)�n�AD�ii2Dn�sini�nsinrn�··A·Cn>n�e�r��2en2�n2sin2i���(i)n�·B2明纹�(i)�k�,k�1,2,3,�暗纹������i�2k��1,k��0,1,2,�2�倾角i相同的光线对应同一条干涉条纹---等倾条纹.\n�2.应用:反射光2反射光1•光束1、2的光程差�n��n>n�e��2ne�2n�•增反膜���2ne��k�2---明纹,反射加强,透射减弱.例:滤光片•增透膜�2k�1��2ne���22---暗纹,反射减弱,透射加强,例:照相机,助视器\n1.透镜表面通常覆盖着一层MgF�n=1.38小于透22镜的折射率�的透明薄膜�为的是利用干涉来降低玻璃表面的反射�为使氦氖激光器发出的波长为632.8nm的激光毫不反射地透过�试求此薄膜必须有多厚�最薄厚度为多少��设光线垂直入射�解�n1n3,�1为入射光在折射率为n的媒质中的波长�则两束反射光在相迂点1的位相差为�n1(A)2�nen�211ne(B)4nen2121n3(C)4�nen���2112�2��������2ne�真空�(D)4�nen�2�n�2211真空11[C]\n六.薄膜干涉(二)---等厚条纹�入射光(单色平行光垂直入射)1.劈尖(劈形膜)反射光2反射光1n�·AA:1,2的光程差:ne��n�(设n>n�)�(e)�2ne��4�52��10~10rad明纹�L�(e)�k�,k=1,2,3,…暗纹明纹暗纹��e��(e)�(2k��1),k�=0,1,2,…�2ekek+1--------等厚条纹\n①条纹间距:L�e�eL��sin��明纹暗纹2n�e���e���L�ee2n�kk+1•上膜上移,条纹?•波长变大;复光照射•夹角变大;折射率变大;条纹?\nSiO②劈尖的应用2�L�2n��测波长;�测折射率;d�测细小直径、厚度、微小变化;Si�测表面不平度等厚条纹平晶λ平晶标待准测Δh块块规规待测工件\n1.用劈尖干涉法可检测工件表面缺陷�当波长为�的单色平行光垂直入射�若观察到的干涉条纹如图所示�每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切�则工件表面与条纹弯曲处对应的部分��A�凸起�且高度为�/4��B�凸起�且高度为�/2��C�凹陷�且深度为�/2��D�凹陷�且深度为�/4。空气劈尖平面玻璃[C]工件\n2.平板玻璃构成一空气劈尖�l=4cm�一端夹住一金属丝,�=589.0nm的钠光垂直入射:�若观察到相邻明纹间距离L=0.1mm,求①金属丝的直径d=�②将金属丝通电受热膨胀,直径增大�在此过程中�从玻璃片上方离劈棱距离为l/2的固定观察点上发现干涉向左移动2条�金属丝的直径膨胀了多少���B解:①L�tg����d/l2n�dl�A�/2�C�d��0.1178mml2L②向左移两个条纹,该处厚度增加2��/2d589nm\n2.牛顿环o牛顿环R显微镜装置简图re分束镜M.S�平凸透镜平晶o光程差�2ne��2e�22222rr�R�(R�e)�2Re�e�2R\no暗环�R����2e��(2k�1)22re�第k个暗环半径rk�kR��k明环�����2e��k�22k�1�第k个明环半径rk�R��k2①条纹变化:•复光照射;中心圆环;透镜上移条纹?•折射率变大,条纹?\no②牛顿环的应用Rr�kR�rek22r�r�mR�k�mk�•测透镜球面的半径R�已知�,测m、r、r,可得R.k+mk�•测波长λ�标准验规已知R�测出m,rk+m,rk,可得λ.待测透镜•检验透镜球表面质量暗纹\n1.单色光AB空气CDE[B]\n2.如图所示,牛顿环装置的平凸透镜与平板玻璃有一小缝隙e�现用波长为�的单色光垂直照射�0已知平凸透镜的曲率半径为R�求反射光形成的牛顿环的各暗环半径。解�设某暗环半径为r�根据几何关系�近似有2e�r2Re干涉减弱条件:e空气011��2e�2e���2k�1�022�r�Rk��2e(k为整数,且k�2e0�)0\n.M2M�11.仪器结构、光路2G1GM2.工作原理21S1光束2′和1′发生干涉半透半反膜�若M�1、M2平行�等倾条纹2�1�E�若M�1、M2有小夹角�等厚条纹若M平移�d时,干涉条移过N条:十字叉丝1λ�d�N�23.应用��微小位移测量�测折射率等厚条纹\n1.dnM2(A)2(n-1)d;M�12(B)2nd;G1G2M1(C)2(n+1)d+/2;S1(D)nd;半透半反膜(E)(n1)d.2�1�E[A]\n一.衍射现象1.现象:光绕过障碍物进入几何阴影区的现象衍射屏观察屏衍射屏观察屏a�103�L�L�S�S*a*2.分类:•菲涅耳衍射近场衍射•夫琅和费单缝衍射•*夫琅和费圆孔衍射•夫琅禾费衍射远场衍射•光栅衍射(平行光)•*x射线衍射\n.Huygens原理�传播方向强度分布�Fresnel补充�“……�波场中任一点的强度由各子波在该点的相干叠加决定。”惠�菲原理�波的传播方向及强度分布衍射的本质�同一波阵面各点发出的子波在障碍物几何阴影区相干叠加\n*子波源的相干叠加,决定该点波的强度.C�K(�)2�rnE(p)��cos(�t�)�dSdE(p)sr��rdS··pQ�E�cos(�t��)0(p)�p)S(波前)*P处波的强度:I�E2设初相为零p0(p)例2.惠�菲原理的基本内容是�波阵面上各面积元所发出的子波在观察点P的�决定了P点的合振动及光强。\n.观察屏0缝平面.0透镜L170透镜L�p.0·47B�a��S*00.0A4δ7f�0.017f•衍射角为�的光线的相干叠加�p点处的光振动\n�A→P和B→P的光程差:asin00——中央明纹(主极大)1.半波带法:asinθ1B21′1半波带2′2半波带a1′半波带2′半波带Aλ/2�两个半波带上光在P处干涉相消�形成暗纹•菲涅耳将AB处波阵面分成许多等面积的波带——半波带.\n•作用�两相邻半波带上各点发出的衍射角为�的光线两两相消•结果�若AB为偶数个半波带,则p点为暗纹;若为奇数个半波带,则p点为明纹.•半波带的数目随�角的不同而改变asin32BθBθ�可将缝分成三个a半波带,P处近似为a明纹中心Aλ/2Aλ/2asin2�可将缝分成四个半波带,形成暗纹.\n1.,.30,3,.3asin30a32\n2.条纹位置x2��xΔx•暗纹(极小):1�1Δx0��asin���k��k�1,2…0���0��sin���k--角位置kkaff�x�fsin���k--线位置kka•明纹(次极大):���asin���(2k��1)�k��1,2…2��k��sin�k���(2k��1)--角位置2a�xk��fsin�k���f(2k��1)--线位置2a\n3.条纹宽度•中央明纹宽度�x2f��x1Δx�x�x�x�2�0�1暗�1暗�aΔx00•其它明纹宽度�1��f0�x�x�x��k�1暗k暗af①�x=2�x0②若缝宽a>>�,则�x�0,衍射消失.设f=50cm若a=102���x=5mma=103���x=0.5mma=104���x=0.05mm单缝衍射�a~0.1mm(~200�)\n•白光照射,中央为白色,两侧对称分布形成衍射光谱.4.条纹强度1I/I0相对光强曲线0.0170.0470.0470.017-2�-�0�2�asin�•条纹的确切位置:0(主极大)asin�=�1.43�,�2.46�,�(次极大)��,�2�,�(极小)•半波带法对强度分布的解释\n例1.,=600nm,a=0.60mm,f=60cm,.x2f1.2mm0ad3x3.6mm00d\n例2.,,观察屏缝平面透镜L·透镜L�pB�S*a�0Aδf�f\n例3.已知a=0.5mm�f=50cm�白光垂直照射,在x=1.5mm处看到明纹极大,求入射光的波长及衍射级数�单缝所在处的波阵面被分成的波带数目。解�•明纹位置�x�fsin���f(2k��1)�k�k�2a�3�332ax/f2�0.5�10�1.5�103�10����nm�22k�1(2k�1)�50�102k�1•白光波长400—700nm•k=1时,λ1=1000nm�•可分成的波带数�•k=2时,λ2=600nm符合题意�•N=�2k+1�=5•k=3时,λ3=428.6nm符合题意�•N=7•k=4时,λ4=333.3nm。\n1.圆孔的夫琅禾费衍射观察屏相对光1I/I0衍射屏L�强曲线�1中央亮斑(爱里斑)01.22�dsin�圆孔孔径为df爱里斑dsin1.2211.22λd�爱里斑变小θ�1d��\n2.光学仪器的分辨本领——对相邻点状物的分辨能力刚可分辨不可分辨非相干叠加瑞利判据:对于两个光强相等的不相干的点物�若其一个衍射光斑的中心恰好落在另一的边缘(第一暗纹处),被认为是刚可分辨。\n刚可分辨不可分辨d�1S1L*�0△xRI*S2Δxλ最小分辨角θR==θ1�1.22Ld1d分辨本领R���1.22�R望远镜��不可选择�可�d��R显微镜�d不会很大�可����R\n•光学镜头直径越大,分辨率越高.一般天文望远镜的口径都很大,世界上最大的天文望远镜在智利,直径16米,由4片透镜组成.\n•采用波长较短的光�也可提高分辨率。电子显微镜用加速的电子束代替光束�其波长约0.1nm,用它来观察分子结构。电子显微镜拍摄的照片\n例1.人眼瞳孔直径约3mm�可见光的平均波长5500Å�人眼的最小分辨角是多大���4解���1.22�2.2�10rad�0.8�Rd①在黑板上划一等号�要使离黑板15m远的同学能够看清�则等号的两横线的间距至少多大��x����x�L��3mmRRL\n②电视画面有420条水平线,若用29��的电视机收看节目,则在距电视机多远的范围内能看清画面�相邻水平线间距:31�x�29�25.4���1.1mm5420�x�x���L��5mRL�R\n*人眼、显微镜、照相物镜的分辨率1.人眼n=1n'=1.336设人眼瞳孔直径为D�2�y��1'玻璃体折射率为n’���'12'可把人眼看成一枚凸L透镜�焦距只有20毫米�其成象实为夫琅和费衍射的图样。由瑞利判据得���’=1.22�’/D=1.22�/(n’D)折射定律�n�sin(��)�n'sin(��'),n�(��)�n'(��')�����'�n'/n�1.22�/n'D�(n'/n)�1.22�/D所以���=1.22�/D所以���为眼外两个恰可分辨的物点对瞳孔中心所张的角�称为眼外最小分辨角。\n2.照相物镜的分辨本领一般对远近不同物体拍摄时�其象距总是和镜头焦距f’很接近�类似人眼的讨论�物镜恰可分辨的两个象点的最小间距为��y'=f'•��'=f'(1.22�/D)D是物镜的有效孔径�照相机底片处每毫米所能分辨的最多刻线数为�N=1/�y'D/f’称为物镜的相对孔径。其倒数俗称光圈一般的胶卷颗粒大小只能分辨每毫米200刻痕左右�这相应使用光圈为8�来拍摄所能分辨的刻痕数。\n.1.:大量等宽等间距平行狭缝构成的光学元件透射光栅(玻璃)�反射光栅(金属)�透光addb不透光a+b�d(~1�m)——光栅常数100mm刻104--106条刻痕\n光栅衍射�单缝衍射�多缝干涉2.-3级3级-2级-1级0级1级2级(白)明纹(谱线、主极大)——很窄、很亮、间距很大IIN=40dsin�-2�-�0�2�-(�/4)�/4\n3.观察屏光栅透镜LP��d�o焦距fdsin�光栅缝数----N,光栅常数----d相邻光束间光程差:dsin(ab)sin\n光栅观察屏透镜LP•明纹(主极大)条件���ddsink�o(k=0,1,2,…)------光栅方程dsin�焦距fk=1,第一级谱线EpNEpk=2,第二级谱线…x•因d很小�谱线�通常较大�sintgf:d=3=19�,=42�,=90�123\n例1.一衍射光栅对某波长的垂直入射光�在屏幕上只能出现零级和一级主极大�要使屏幕上出现更高级次的主极大�应该(A)换一个光栅常数较小的光栅。(B)换一个光栅常数较大的光栅。(C)将光栅向靠近屏幕的方向移动。(D)将光栅向远离屏幕的方向移动。B(ab)sink(ab)k\n例2.在450~650nm之间的复色平行光垂直照射在每厘米有5000条刻线的光栅上�屏上第二级光谱各色光所占范围的宽度为35.1cm�求透镜的焦距。解�光栅常数�a�b�1�10�2�2�10�6(m)5000第二级光谱满足:(ab)sin2光栅观察屏透镜LP�=450nm:�=26.74�→x=f�tg���1111d�o�2=650nm:�2=40.54�→x2=f�tg�2焦距fdsin��2x�x35.1�1021�f���1.00(m)tgθ�tgθtg40.54��tg26.74�21如用sin��tg�=x/f�则得f=1.76m.\n3144224113����/2�������3�/2N����2k��kdsind�sin�N����2��k��1,2,…(k��Nk,k�0)•相邻主极大间有N�1个暗纹和N�2个次极大.\n例N=4,有三个极小k��1,k��2,k��3*(N=4)光强曲线IIN=40dsin�-2�-�0�2�-�/4�/4主极大间距暗纹间距=N\n4.(N=4,d=4a)II单0单单缝衍射光强曲线-2-1012sin�(�/a)多光束干涉光强曲线N2-8-4048sin�(�/d)IN2I0单光栅衍射单缝衍射光强曲线轮廓线(�/d)-8-4048sin�\n例1.双缝衍射中,保持双缝的中心距不变,而把两条缝的宽度略微加宽�则(A)单缝衍射中央主极大变宽�所包含干涉条纹数目变少.(B)------------------------------宽�-----------------------------多.(C)-----------------------------宽�----------------------------不变.(D)------------------------------窄�-----------------------------少.(E)----------------------------变窄�-----------------------------多.N2I0单光栅衍射单缝衍射光强曲线轮廓线-8-4048sin�(�/d)答�(D)两缝中心距不变�则条纹位置不变�缝宽增大�则单缝衍射的中央主极大变窄�\n例2.在双缝干涉实验中�两条缝的宽度原来是相等的�若其中一缝的宽度略变窄�则(A)干涉条纹的间距变宽。(B)干涉条纹的间距变窄。(C)干涉条纹的间距不变,原极小处的强度不再为零。(D)不再发生干涉现象。答�(C)因两缝中心距不变�故条纹位置不变�因而条纹间距不变�但其中一缝变窄后�两束光波强度不等�在干涉相消处�强度不再为零。\n5.IN2I0单光栅衍射单缝衍射光强曲线轮廓线-8-4048sin�(�/d)-3级3级光栅光谱-2级-1级0级1级2级(白)谱线位置�dsin���k�衍射暗纹位置�asin���k���a�b谱线缺级级次:k�k�a------当k�取某些非零整数使k为整数时,k级谱线缺失.\n3.,(a+b)(a)k=3,6,9(A)a+b=2a(B)(B)a+b=3aab(C)a+b=4akk(D)a+b=6aa\n例4.波长为700nm的单色光,垂直入射在平面透射光栅上,光栅常数为3×10-4cm,缝宽为10-4cm.求(1)最多能看到第几级光谱?(2)能看到几条谱线?:(1)�dsin���k��kmax�d/��4.28取整�即最多可看到第四级光谱谱线d(2)满足k�k'�3k�----第三级出现缺级a即光屏上实际有七条谱线对应于明纹k=-4,-2,-1,0,1,2,4�4�2�10124\n*6.——区分波长相近的谱线的能力λ的k级主极大λ+�λ的k级主极大k�sin��dsin�k�������对应k��Nk�1的������的暗纹sin��Nd�•定义R�•计算RkN光栅缝数��谱线级次\n例5.钠黄光包含两种波长成分��=5890Å�1�=5896Å�若想在第三级谱线处分辨出来�则2光栅的缝数至少应为多少�λ解�kNλλ21λN327.4k(λλ)21故缝数至少应为328条\n7.⑴单色仪(monochrometer)把复色光中某一波长成分分离出来�光谱分析e.g.Ramanspectroscopy⑵光栅光谱仪(gratingspectrograph)测出物质发光的波长成分及其相对强度�元素分析e.g.矿物、天体\nX射线管*XKA+-1.X射线的产生X射线�:10-1�102劳厄实验�1912�准直缝晶体劳厄·斑X射线·证实了X射线的波动性··2.X射线在晶体上的衍射:掠射角12��AC�CB�2d�sin�晶面��������d��散射光干涉加强条件�d��A�B���Cdsin�������2d�sin��k�(k�1,2,�)������--—布喇格公式������d�3.应用d:晶面间距(晶格常数��已知�、�可测d—X射线晶体结构分析。�已知�、d可测�—X射线光谱分析。\n------偏振是横波的表现一.光的偏振现象1.自然光传播方向E·面面对光的传播方向看没有优势方向自然光的分解振动�自然光可分解为两束振动方向相互垂直的、等幅的、不相干的线偏振光.1ExEyI0�Ix�Iy�Ix�Iy�I02�自然光的表示法�···\n2.光的偏振现象•偏振现象·①线偏振光(完全)•线偏振光的表示法�线偏振光·····光振动垂直板面光振动平行板面②部分偏振光没有优势方向自然光的分解•部分偏振光的表示法�•不等幅的,不相干的线偏振光合成.········平行板面的光振动较强垂直板面的光振动较强有优势方向部分偏振光\n③圆偏振光yEEy�E�Ecos(�t��)�·�xxx�Ex��Ey�Esin(�t��y)y线偏振光传播方向yEx0x右旋圆z偏振光�/2某时刻右旋圆偏振光E随z的变化④椭圆偏振光�E�Ecos(�t��)�xax���E�Esin(�t��)右旋椭圆yby偏振光\n.非偏振光线偏振光�起偏器:获得偏振光的器件···电气石晶片�原理:利用某种光学不对称性1.:光的二向色性P自然光I0线偏振光I12.···I�I0①反射和折射时光的偏振偏振化方向2(透振方向)·线偏振光··n···i0i0···n···ii···i+r=9001·100n2r0n2rnsininsinr··1020起偏振角自然光反射和折射ncosi20后产生部分偏振光n2tgi��n021�i=i0,i0:布儒斯特角n1\nn�布儒斯特定律(1812年)2tgi��n021n1若n=1.00(空气),n=1.50(玻璃),则�12�11.50�空气→玻璃i�tg�56�1801.00���互余�11.00�玻璃→空气i�tg�33�420�1.50�······i0············自然光从空气→玻璃············I��7%I玻璃片堆0(接近线偏振光)\n1.�E··n··i0i0···1·n2r0·90起偏振角\n3.102°Ae自然光in1······on2光轴re方解石晶体Gaco3re光oo光B(各向异性媒质)�寻常光和非寻常光o光:遵从折射定律n1sini�n2sinrosini�conste光:一般不遵从折射定律sinree光折射线也不一定在入射面内.�晶体的光轴:不发生双折射,称为光轴.平行此方向也为光轴.\n�主平面和主截面·o光的e光的·主平面主平面·主平面:光传向与光轴·o光e光光轴光轴主截面�晶体表面的法线与光轴.吸收涂层�方解石o光轴ie············光轴方解石加拿大树胶�(n=1.55)o光、e光对应nno、eno(1.6584)�n(1.55)�ne(1.4864)\n③圆和椭圆偏振光的产生�晶片─相位延迟片yAeAxλ�Ao线偏振光d通过厚为d的晶片�o、e光产生相位差����四分之一波片ne�no�d�����42��二分之一波片ne�no�d������2\n.P�偏振器:分析、检验光的偏振态待检光I2II0cos?---马吕斯定律(1809)PI0�I0�IIImax0����I�0---消光2EP0•I不变��是什么光自然光�•I变�有消光��线偏振光E=E0cos�•I变�无消光��部分偏振光\n自然光四自然光偏线偏振光振I不变分之片圆偏振光一线偏振光�线偏振光波转I变,有消光片动�以入射光方向为轴部分部分偏振光四偏振光偏线偏振光振I变,无消光分之片椭圆偏振光一线偏振光�线偏振光波转I变,有消光片动�光轴平行最大光强或最小光强方向放置或光轴平行椭圆偏振光的长轴或短轴放置\n1.I045PI=I/210PI=Icos245=I/420P1自然光I0线偏振光I�P2I’···偏振化方向(透振方向)1I�I02\n180(A)(B)(C)(D),,,.P1自然光I0线偏振光I�P2I’···偏振化方向(透振方向)(B)\n1.n’=1.68n=1.38MgF2�=500nm(1nm=10-9m)MgFn2A90.6nm;B78.1nm;C181.2nm;D156.3nm.�n(A)��2ne�2k�112n�2MgF2e��90.6nmBn4n3\n⒉如图�单色光波长为��将一折射率为n、劈角为�的透明劈尖插入光线2中�则当劈尖缓慢上移时(只遮住S)�屏上干涉条纹2(A)间隔变大�向下移动。�S11(B)间隔变小�向上移动。S2(C)间隔不变�向下移动。2(D)间隔不变�向上移动。(C)r2r10D�x��r(n1)drd21\n3.如图,两个彼此平行的滚柱夹在两块平晶之间形成空气劈尖,当单色光垂直入射时,产生等厚条纹.若滚柱之间距离变小,则在此范围内,干涉条纹的(A)数目减少�间距变大。(B)数目不变�间距变小。(C)数目增加�间距变小。(D)数目减少�间距不变。答�(B)2dk1122dk222\n4.在迈氏干涉仪的一支光路中放一片折射率为�的透明介质薄膜后�测出两束光的光程差的改变量为��则薄膜厚度为�����2�����(2n)�����n�����2(n-1)(D)2(n1)d\n5.在双缝干涉实验中�屏幕上�点是明条纹�若将缝S2盖住�并在S1、S2连线的垂直平分处放一反射镜M�则此时��SP1����点仍为明条纹S*����点为暗条纹SM2�C�无干涉条纹�D�不能确定�点是明条纹还是暗条纹答�(B)\n6.两块平玻璃构成空气劈尖,用单色平行光垂直入射.若上面的平玻璃慢慢地向上平移,则干涉条纹(A)向棱边方向平移�条纹间隔变小。(B)向棱边方向平移�条纹间隔变大。(C)向棱边方向平移�条纹间隔不变。(D)向远离棱边的方向平移�条纹间隔不变。(E)向远离棱边的方向平移�条纹间隔变小。答��C�ek劈尖中对应于一定空气隙厚度的位置向棱边方向移�动�故条纹向此方向平移L�2n�\n7.双缝装置放在空气中,光波长为�,已知P点处为第三级明纹,则S和S到P点的光程差为;若将装12置放在某种透明液体中,此时P点为第四级明纹�则该液体的折射率n=.解�prr3�S121n(r2r1)4S24n3\n8.折射率为1.60的两块平玻璃板之间形成一个劈尖�用�=600nm(1nm=10-9m)的单色光垂直入射。假如在劈尖内充满n=1.40的液体时相邻明纹间距比空气劈尖缩小0.5mm�则劈尖角�=.解�充满空气时�间距l/21充满液体时�间距l/2n2(n1)1.710�4rad2n(ll)12\n9.在牛顿环的平凸透镜和平板玻璃间充以某种透明液体,发现第10个明环的直径由充液前的14.8cm变成充液后的12.7,求液体折射率n.解�充液前�明环半径r(k1)R2充液后�明环半径r(k1)R/n2r/rnrdn()2()21.36rd\n10.用波长为�的平行单色光垂直照射如图所示的装置�观察空气薄膜上下表面反射光形成的等厚干涉条纹�试在图下方的方框内画出相应的暗纹�表示出它们的形状、条数和疏密。解�由条纹的等厚性知�条纹应为环状。�=2e+�/2=(2k+1)�/2球面7�/4边缘处��=�/2—暗纹�L�2n�,.\n11.在n=1.50的玻璃上�镀上n�=1.35的透明介质薄膜。垂直照射�观察反射光的干涉�发现对�=6000Å的光波干涉相消�对�=7000Å的光波干12涉相长�且在两者之间没有别的波长是最大限度相消或相长的情形。求所镀介质膜的厚度。解�光程差�=2n�eair按题意2ne(2k1)1n�e2n当�增至�时�(2k+1)/2减至k�即有12��2nek�e�12�7.78�10�7m24n�(���)21\n12.如图�斜入射�则P点处两相干光的光程差为。S1r1P�dr2�S2解�=r-(dsin+r)=r-r-dsin2121\n13.如图�两块平板玻璃一端接触�另一端用纸片隔开�形成一空气劈尖。用单色光垂直照射�观察透射光的干涉条纹。⑴设A点处空气薄膜厚度为e�求发生干涉的两束透射光的光程差。⑵在劈尖顶点处�透射光的干涉条纹是明纹还是暗纹�解�⑴两束透射光中�一束在劈尖上下表面都经历了反A射�有两次半波损失�另一束未经历反射。光程差�⑵在顶点处�明纹\n14.双缝实验,�=5893Å,相邻明纹的角距离(即相邻明纹对双缝中心处的张角)��=0.20�.⑴要使��增大10%,�=�⑵若将装置浸入水中(n=1.33),��=�解�⑴sink+1级kk��k级dkkd�kd(k1)k�1/d//(/)(110%)58936482(Å)\n⑵浸入水中�则有ndkk类似于⑴�可得0.200.15ndn1.33\n1.=300=5000A[]2.510-7m2.510-5m1.010-6m1.010-5m\n2.1mm2m2mm[]10000A4000A5000A6000A\n3.ab[]a=ba=2ba=3bb=2a\n4.=5500Ad=210-4cm[]2345\n5=450nm=750nm12[]22345…25811…2468…36912…\n6.l=500nm�a=0.25mmd=12mmf(A)2m(B)1m(C)0.5m(D)0.2m(E)0.1m\n7=5500Aa=4=300_____8,2.\n96250A800____.\n10.,=0.668m=201=0.447m2\n11.用每毫米有300条刻线的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱。已知红谱线波长在0.63~0.76�m范围内�蓝谱线波长在0.43~0.49�m范围内。当光垂直入射时�发现在衍射角为24.46�处�红、蓝两谱线同时出现。⑴如果还有的话�在什么角度下还会出现这种复合谱线�⑵在什么角度下只有红谱线出现�\n1.I0=600II01/43/41/83/8\n2.600,,[](�)完全偏振光�且折射角是300(B)部分偏振光且只是在该光由真空入射到折射率为3的介质时,折射角是300(C)部分偏振光,但须知两种介质的折射率才能确定折射角(�)部分偏振光�且折射角是300\n3.I0PPPI8PP1、2、3013P2P[]2300450600900\n45\n5SSSP121PPP212\n(n=1.00)(n=1.60)12iirⅠiⅡrⅠ\n1.3331.517,=?i1i2\n1.=300=5000A[]2.510-7m2.510-5m1.010-6m1.010-5m�6:Casinka21.010m\n2.1mm2m2mm[]f10000Ax24000Aaax5000A510�7m6000A2f:C\n3.ab[]a=ba=2ba=3bb=2adab:A2aa\n4.=5500Ad=210-4cm[]2345d:Bdsinkk3.6max\n5=450nm=750nm12[]2dsink2345…11dsink25811…222468…36912…k3:Dk11k(k5,10,15�)21152\n6.l=500nm�a=0.25mmd=12mmf(A)2m(B)1m6fxx6x3�3(C)0.5ma(xx)a(D)0.2mf3�31m(E)0.1m6:B\n7=5500Aa=4=300__4___1:asin4428,2300.1:asinksina2300\n96250A800____.:dsink1mm1dsin300800d2\n10.,=0.668m=201=0.447m2k2dsinkk121122k321dk=2,k=3.122d13.9110�6mminsin\n11.用每毫米有300条刻线的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱。已知红谱线波长在0.63~0.76�m范围内�蓝谱线波长在0.43~0.49�m范围内。当光垂直入射时�发现在衍射角为24.46�处�红、蓝两谱线同时出现。⑴如果还有的话�在什么角度下还会出现这种复合谱线�⑵在什么角度下只有红谱线出现�dsinkdsink0.63m0.76mk=2,=0.690mR0.43m0.49mk=3,=0.460mBk=kRRBB\nk22RBkkk2,4,6,�k3RBRBR3ksin1k455.90dRmaxk=4Rk=1,3.R11.90,k1k1sind38.40,k32\n12.(A)1.010-1mm(B)5.010-1mm(C)1.010-2mm(D)1.010-3mmdsin��k�dk..dcos�����k�����ctg�����\nkk=1dd>,(=0.4~0.76m)d.(D)\n1.I0=600II01/43/41/83/8:CP1自然光I0线偏振光I�P2I’···偏振化方向(透振方向)120I�II��Icos60�I8002\n2.600,,[](�)完全偏振光�且折射角是300(B)部分偏振光且只是在该光由真空入射到折射率为3的介质时,折射角是300(C)部分偏振光,但须知两种介质的折射率才能确定折射角线偏振光··(�)部分偏振光�且折射角是300n··i0i0····1n2r0:D·起偏振角\n3.I0PPPI8PP1、2、3013P2P[]2300450600900P1自然光I线偏振光I�P2I’I’’0···偏振化方向12I�I0I��Icos�222Icos�sin�20:BI���I�cos���I082\n45:自然光I0+I’P111···I�I�I�I�I�最小0最大0偏振化方向22I最大I01�5��I最小I�2\n5SSSP121PPP212:\n(n=1.00)(n=1.60)12iirniarctg258.0Ⅰi0n1Ⅱrr90i32.0Ⅰ=r\n1.3331.517,=?i11.333i�arctg�53.12�11.000i21.517i�arctg�48.69�21.333���180��90��(90��i)�(90��i)�11.81�12