大学物理作业解答 24页

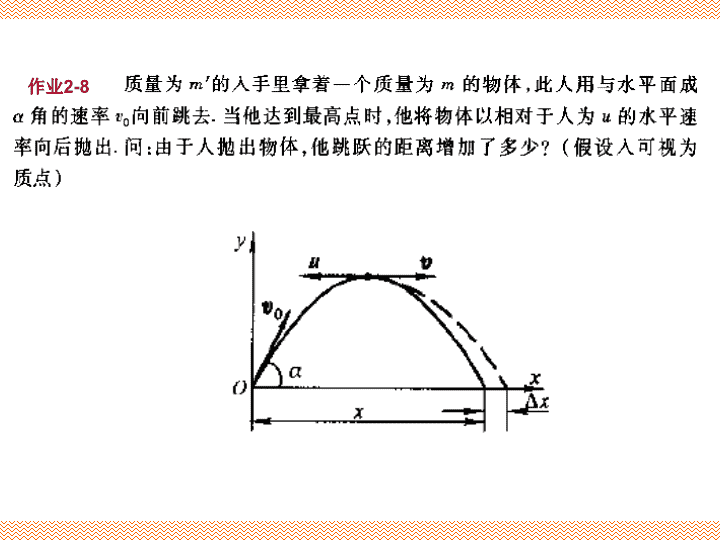
作业2-8\n\n\n练习4-2（1）假设子弹离开枪口时合力刚好为零\n\n已知地球质量为M，半径为R。现有一质量为m的人造卫星在离地面高度2R处，以地球和卫星为系统，若取地面的引力势能为零，则系统的引力势能为多少？若取无限远处引力势能为零，则系统的引力势能又为多少？系统引力势能等于将物体由场点移动到零势点过程中，保守内力做的功补充解法提要取地面为引力势能零点，则系统引力势能为取无限远处为引力势能零点，则系统引力势能为\nORABNGvMV解：m在下滑过程中，机械能守恒；且系统在水平方向上不受外力，系统动量也守恒:\nNORABNGvMVmgv’物体m下滑至B处时，M所受合外力为零，没有加速度，所以M是惯性系，则相对此惯性系可写出对m的牛二定律方程∶物体m至B处时相对M的水平速度为：\n作业5-2(3)劲度系数为k的轻弹簧，一端固定在墙上，另一端连在一个质量为m的物体上，如图所示，物体与桌面间的摩擦系数为μ。初始时刻弹簧处于原长状态，现用不变的力F拉物体，使物体向右移动，求物体将停在何处？此时系统弹性势能是多少？解：以物体、弹簧为系统，由功能原理得\n作业5-3：一链条总长l，质量为m，放在桌面靠边处，下垂一端长为a，链条与桌面的滑动摩擦系数为，链条由静止开始运动。求：(1)链条离开桌边过程中，摩擦力对链条作的功？(2)链条离开桌边时的速度？Nfr解∶绳线密度λ=m/l,绳下垂x长时绳与桌面间的摩擦力将绳、桌面、地球看作系统,则非保守内力fr作的功等于系统机械能的增量\n作业5-3：一链条总长l，质量为m，放在桌面靠边处，下垂一端长为a，链条与桌面的滑动摩擦系数为，链条由静止开始运动。求：(1)链条离开桌边过程中，摩擦力对链条作的功？(2)链条离开桌边时的速度？Nfr\n解：\n\n0r0vom2-19、如图，一细绳穿过光滑水平桌面上的小孔o，绳的一端系有一质量为m的小球并放在桌面上；另一端用力往下拉住。设开始时小球以角速度0绕孔o作半径r0的匀速圆周运动,现在向下拉绳，当小球半径减少到r0/2时，向下拉的速度为v，求这一过程中拉力的功。\n0r0vom解小球所受的力中,重力和桌面的支持力抵消,只有绳的拉力影响小球的运动。拉力的作用线通过o点,对o点的力矩为零,故小球在运动中对o点的角动量守恒,于是有由动能定理，拉力的功为\n解∶取小球与地球为系统，机械能守恒:由角动量守恒,得联立解得2-22质量为m的小球A，以速度沿质量为M，半径为R的地球表面切向水平向右飞出。OC=3R。求C点的速度。(略空气阻力及地球自转。)\n解：在一轻弹簧下端悬挂砝码时，弹簧伸长8cm，现在这根弹簧下端悬挂m=250g的物体，构成弹簧振子。将物体从平衡位置向下拉动4cm，并给以向上的21cm/s的初速度（这时t=0）。选x轴向下，求振动方程的数值式。\n在竖直面内半径为R的一段光滑圆弧形轨道上，放一小物体，使其静止于轨道的最低处。然后轻碰一下此物体，使其沿圆形轨道来回作小幅度运动，试证：（１）此物体作简谐振动；（２）此简谐振动的周期。解：（１）当小物体偏离圆弧形轨道最低点角时，其受力如图所示，切向分力物体作简谐振动很小\n在竖直面内半径为R的一段光滑圆弧形轨道上，放一小物体，使其静止于轨道的最低处。然后轻碰一下此物体，使其沿圆形轨道来回作小幅度运动，试证：（１）此物体作简谐振动；（２）此简谐振动的周期。解：（2）周期\n解：（1）由已知条件，谐振动的角频率为最大速度最大加速度\n（2）设振动方程为由题意，，则此时的速度为加速度回复力\n（3）振子速度具有正最大值，是位于平衡位置向正方向运动，由旋转矢量法可知所以振动方程为\n32-4:已知入射波表达式在x=0处发生完全反射，反射点为固定端，试写出：⑴反射波表达式；⑵合成波表达式；⑶波节与波腹的位置。解：⑴已知x=0处为固定端反射点，入射波在x=0处的振动为因有半波损失，反射波在x=0处的振动为由入射波表达式知，入射波沿x轴负方向传播，故反射波沿x轴正方向传播。由y20得反射波表达式为\n⑵合成波表达式为⑶波节满足所以波节位置为波腹满足从而相应解出波腹位置为