大学物理课件 66页

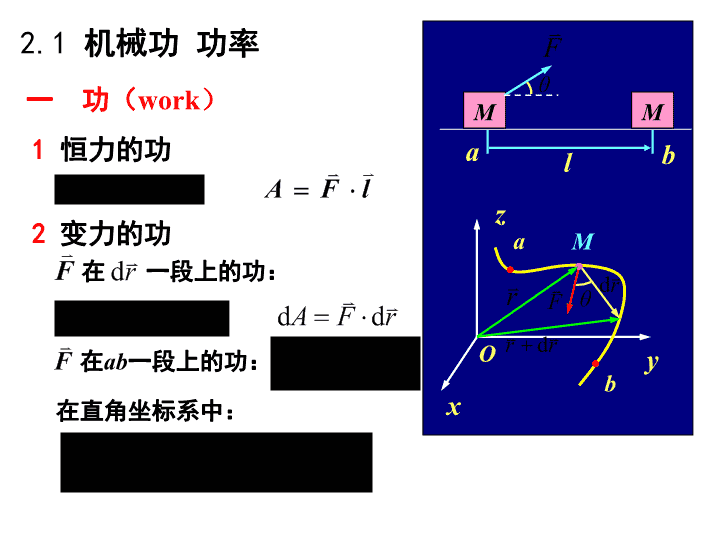
第2章质点力学的守恒定律1）从力对空间的积累作用出发，引入功、动能的概念----能量守恒定律2）从力对时间的积累作用出发，引入动量、冲量的概念----动量守恒定律三大守恒定律是普适的，守恒定律更重要3）介绍角动量、动量矩---引入角动量守恒定律牛顿定律是瞬时的规律，有时需关心过程中力的效果\n2.1机械功功率一功（work）2变力的功MMablxyzOab一段上的功：M在1恒力的功在直角坐标系中：在ab一段上的功：\n说明(1)功是标量，且有正负(2)合力的功等于各分力的功的代数和(3)一般来说，功的值与质点运动的路径有关二功率瞬时功率：平均功率：\n例1一质点受变力作用，求（1）质点沿OMQ运动时变力所作的功。（2）质点沿OQ运动时变力所作的功。y(m)x(m)33QMo\ny(m)x(m)33QMo\n质量为10kg的质点，在外力作用下做平面曲线运动，该质点的速度为解在质点从y=16m到y=32m的过程中，外力做的功。求例2,开始时质点位于坐标原点。\n2.2动能动能定理（kineticenergytheorem）一.质点动能定理作用于质点的合力在某一路程中对质点所作的功，等于质点在同一路程的始、末两个状态动能的增量。(1)Ek是一个状态量,A是过程量。(2)动能定理只用于惯性系。说明\n二.质点系动能定理把质点动能定理应用于质点系内所有质点并把所得方程相加有:1)内力和为零,内力功的和是否为零？不一定为零ABABSL讨论2)内力的功也能改变系统的动能。如炸弹爆炸过程内力和为零，但内力做功转化为弹片的动能。\n一轻弹簧的劲度系数为k=100N/m，用手推一质量m=0.1kg的物体把弹簧压缩到离平衡位置为x1=0.02m处,如图所示。放手后，物体沿水平面移动到x2=0.1m而停止。放手后，物体运动到x1处和弹簧分离。在整个过程中，解例1物体与水平面间的滑动摩擦系数。求摩擦力作功弹簧弹性力作功根据动能定理有\n长为l的均质链条，部分置于水平面上，另一部分自然下垂,已知链条与水平面间静摩擦系数为0,滑动摩擦系数为(1)以链条的水平部分为研究对象，设链条每单位长度的质量为，沿铅垂向下取Oy轴。解Oy例2求满足什么条件时，链条将开始滑动(2)若下垂部分长度为b时，链条自静止开始滑动，当链条末端刚刚滑离桌面时，其速度等于多少？当y>b0，拉力大于最大静摩擦力时，链条将开始滑动。设链条下落长度y=b0时，处于临界状态\n(2)以整个链条为研究对象，链条在运动过程中各部分间相互作用的内力的功之和为零，摩擦力的功重力的功据动能定理：Oy\n2.3势能机械能守恒定律一保守力（conservativeforce）xyzO1重力的功重力mg在曲线路径M1M2上的功：(1)重力的功只与始、末位置有关，而与路径无关。(2)质点上升时，重力作负功；下降时，作正功。mG结论②①\nMmrGF=2cos=()Fds90+0θ2.万有引力的功=dAFds.MmrG=2drMmrGsinθ=2dsrabθrdsF太阳地球Mmrdrab))((=abGMmGMmrrMmGA2=rrabdrrò\n万有引力在全部路程中的功为：1)万有引力的功，只与始、末位置有关，与路径无关。结论2)质点移近质点时，万有引力作正功；远离时，作负功。\n3弹性力的功1)弹性力的功只与始、末位置有关，与路径无关2)弹簧的变形减小时，弹性力作正功；增大时，作负功。弹簧弹性力由x1到x2弹性力的功：结论:xO\n力所做的功与路径无关，而只决定于物体的始末相对位置，这样的力称保守力。如重力、万有引力、弹性力4保守力作功与路径有关的力称为非保守力，如摩擦力\n质点在保守力场中某点的势能，在量值上等于质点从该点移动至零势能点的过程中保守力作的功。1重力势能2弹性势能xyzOOx二势能（potentialenergy）\n3万有引力势能rMm等势面保守力的功等于质点在始末两位置势能增量的负值\n2)势能零点可任意选取，故某点的势能值是相对的。3)保守力场中任意两点间的势能差与势能零点选取无关。说明1)只有物体间相互作用力是保守力，才能建立势能的概念。4)势能属于相互作用的物体系统所共有，“某物体的势能”只是习惯的说法。\n重力势能引力势能弹性势能\n质点的势能与位置坐标的关系可用图线表示一维势能曲线zO重力势能弹性势能万有引力势能xOrO\n由势能函数求保守力\n三质点系的动能定理与功能原理AAAmv22112非保内外保内=Σ++Σmvib2ia1、质点系的动能定理：将其推广到质点系，有:AA外内+A==AAA非保内外保内++上式为质点系的动能定理：质点系总动能的增量等于由质点的动能定理：mv22112mv2baA=力的功三者之和。外力的功与质点系内保守力的功和质点系内部非保守\n由质点系的动能定理：ApapbEE=)(保内且：2、功能原理：AAAmv22112非保内外保内=Σ++Σmvib2iaAAmv22112非保内外=Σ+Σmvib2iapapbEE)(AAmv22112非保内外=Σ+Σmvib2iapapbEE)(+(+)kakbEEEE=()+pb(+)pa\n系统的功能原理：AkakbEEEE=()++A外非保内pb(+)pa系统动能和势能之和为系统的机械能，用E表示。E=Ek+Ep则系统的功能原理还可表示为：AA非保内外=+1EE2系统的功能原理表述为：系统机械能的增量等于外力的功与内部非保守力功之和。\n*关于功能原理的讨论：①若则系统的机械能增加；AA非保内外+0>②若则系统的机械能减少；AA非保内外+0<③若则系统的机械能不变。AA非保内外+0=\nAkakbEEEE=()++A外非保内pb(+)pa由系统的功能原理：E==+则：EEEkbpbkapa+恒量机械能守恒定律:如果一个系统只有保守内力作功，四、机械能守恒定律其它内力和一切外力都不作功，则系统的总机械能能保持不变。若：系统的机械能不变。AA非保内外+0=\n能量转换与守恒定律在一个孤立系统内，不论发生何种变化过程，各种形式能量之间无论怎样转换，但总的能量将保持不变。这就是能量守恒定律。*能量守恒定律是自然界中的普遍规律。不仅适用于物的机械运动、热运动、电磁运动、核子运动等物理运动形式，而且也适用于化学运动、生物运动等运动形式。它体现了运动的守恒。\n把一个物体从地球表面上沿铅垂方向以第二宇宙速度据机械能守恒定律有:例1物体从地面飞行到与地心相距nRe处经历的时间。求发射出去，阻力忽略不计，\n用弹簧连接两个木板m1、m2，弹簧压缩x0。解整个过程只有保守力作功，机械能守恒例2给m2上加多大的压力能使m1离开桌面？求\n一质心质心的概念板上C点的运动轨迹是抛物线其余点的运动=随C点的平动+绕C点的转动ccccccc§2—4质心质心运动定律质点体系的质量中心\nm1mim2c\n作用在系统上的合外力等于系统的总质量乘以质心的加速度.二质心运动定律:\n引言：现在来研究力对时间的积累作用一、动量、冲量概念动量状态量、矢量单位：千克.米/秒，kg.m/s冲量单位：牛顿.秒§2-5动量定理动量守恒定律\n二、质点的动量定理分离变量：=mvmv12F=dtdmv()vvtt1212òò它表明作用在物体上的合外力的冲量等于物体动量的增量。质点的动量定理又写成：IP=-P21对一质点而言：两边积分得：【微分形式】\n*关于质点的动量定理的讨论：①式中冲量是矢量，在恒力作用下，冲量的方向与恒力的方向相同。即：②质点的动量定理为矢量式，分量式为：（恒力的冲量）=FtΔIxFdttt12=mvmv12xxòyFdttt12=mvmv12yyòzFdttt12=mvmv12zzò上式说明：哪一个方向的冲量只改变哪一个方向的动量\n三质点系的动量定理1、质点系：由多个质点组成的系统。2、系统的内力和外力系统的内力：质点系内各质点之间的作用力系统的外力：质点系外物体对质点系内质点的作用力3、质点系的动量定理对于质点系内某一个（第i个）质点，由牛二定律可得\n由于系统的内力成对出现，系统的内力矢量和为零。质点系的动量定理：质点系总动量的增量等于作用于该系统合外力的冲量。\n三、质点系动量守恒定律123，，FFF，122113...内力F2F3F1F23F32F31F12F13F21F122对1的作用，，FFF123外力，\n123F2F3F1F23F32F31F12F13F21应用动量原理的微分形式：)+11)mvF1)((dd=tF12++F1333)mvF3()(d=tdF32+F31+vv331122mmv++))(d=FFFmtd3++21(v22)mF2)((d=tdF+F23+21miiv=F(ΣdtdiΣ)\n系统的总动量等于一常矢量，总动量守恒。此式的意义是：作用在系统上外力的矢量和等于系ΣΣ=Fmiiid()dtv即：=cΣmiiv即外力矢量和为零ΣFi=0若：=0Σmiid()dtv则：统的总动量随时间的变化率。\n*关于动量守恒定律的讨论：ΣΣ=Fmixiixd()dtv将上式写成分量式，其中x方向的分量式为：若：Σ=Fix0则有：mixivΣ=c①ΣΣ=Fmiiid()dtv\n②内力的存在只改变系统内动量的分配，而不能改变系③动量守恒是自然界普遍适用的物理定律，它比牛顿④在惯性系中统的总动量。定律更为基本。微观世界的分动量守恒。如果外力在x方向投影的代数和为零，则在x方向⑤内力可以改变系统的动能，但不能改变动量\n例1:质量为10KG的物体,受到力作用,在t=0时,物体静止在原点.求(1)物体在t=10s时刻的动量和动能;(2)从t=0到t=10s内作用力的冲量和所作的功.已知:求:解(1)建立坐标OXYmxY\nmxY(2)求10秒内力的冲量及作的功依冲量的定义:依动能定理:\n§2-7碰撞(Centralcollision)作为动量和能量守恒的具体应用，介绍一下两物体的对心碰撞。碰撞有如下持点。1）碰撞是冲击力，相互作用时间极短，冲击力>>非冲力，可不考虑非冲击力的作用。2）碰撞时间极短，但碰撞前后物体运动状态的改变非常显著，因而易于分清过程始末状态，便于用守恒定律来研究。对心碰撞-----碰撞前后的速度矢量都沿两球中心（质心）连心线上的碰撞。我们把物体视为“球模型”来考虑。\n碰撞前：碰撞后：碰撞过程：m2m1m1m2碰撞过程m2m1m1m2m1m2m1m2m1m2m1m2m1m2(1)压缩阶段：(2)恢复阶段：m2m1m1m2\n1、完全非弹性碰撞：…(1)…(2)…(3)…（4）讨论:A)碰撞后速度B)能量:碰撞前XO碰撞前碰撞后m1m2m2m1m2m1m2m1\n……（4）碰撞前碰撞后结论:有能量损耗.B)能量:\n2、完全弹性碰撞XO碰撞前碰撞后依动量守恒、能量守恒列方程：m2m1m1m2m2m1m2m1\n\n3）一般弹性碰撞XO碰撞前碰撞后m2m1m2m1m2m1两物体碰撞的恢复系数称分离速度，m2相对m1离开时的速度。称接近速度，m1相对m2接近时的速度。引入系数e：其中：（1）定义：m2m1\n测量：m2m1Hh（m1<