大学物理课件 37页

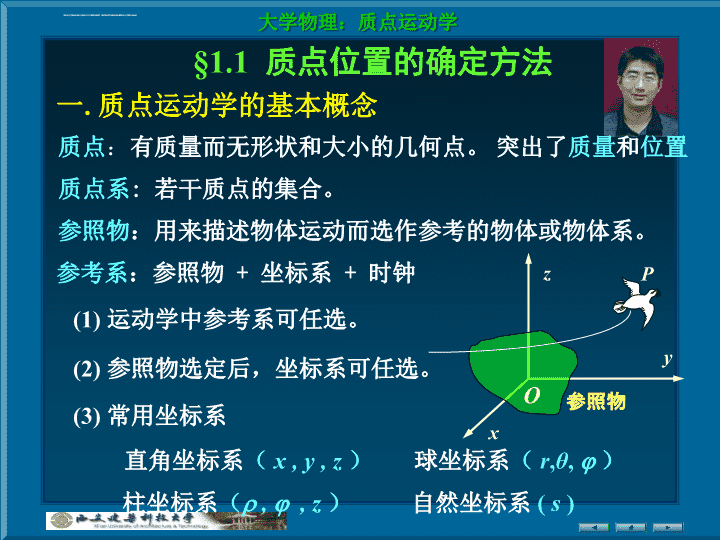
第1章质点运动学激光波长基准装置\n1927年第五次索尔维会议1.1确定质点位置的方法1.2质点的位移速度和加速度1.3用直角坐标表示位移速度和加速度1.4用自然坐标表示平面曲线运动中的速度和加速度1.5圆周运动的角量表示角量与线量的关系1.6不同坐标系中的速度和加速度变换定理简介\n§1.1质点位置的确定方法一.质点运动学的基本概念质点：有质量而无形状和大小的几何点。突出了质量和位置质点系:若干质点的集合。xyzO参照物参考系：参照物+坐标系+时钟(1)运动学中参考系可任选。参照物：用来描述物体运动而选作参考的物体或物体系。P(2)参照物选定后，坐标系可任选。(3)常用坐标系直角坐标系（x,y,z）球坐标系（r,θ,）柱坐标系（,,z）自然坐标系(s)\nyzx参照物二、确定质点位置的常用方法1.直角坐标法P(x,y,z)2.位矢法（质点位置由位置矢量描述）\n表示。位矢的大小为：位矢的方向用方向余弦表示，则有：参考物质点某时刻位置P(x,y,z)由位矢以后各位矢都这样处理\n••3.自然坐标法已知质点相对参考系的运动轨迹时，常用自然法。4.运动学方程(函数)直角坐标下自然坐标下已知运动学方程，可求质点运动轨迹、速度和加速度意义:\n一质点作匀速圆周运动，半径为r，角速度为。以圆心O为原点。建立直角坐标系Oxy，O点为起始时刻，设t时刻质点位于P（x,y），用直角坐标表示的质点运动学方程为位矢表示为例解求用直角坐标、位矢表示的质点运动学方程。\n求解hx坐标表示为例如图所示，以速度v用绳跨一定滑轮拉湖面上的船，已知绳初长l0，岸高h取坐标系如图依题意有质点运动学的基本问题之一，是确定质点运动学方程。为正确写出质点运动学方程，先要选定参考系、坐标系，明确起始条件等，找出质点坐标随时间变化的函数关系。O船的运动方程说明\n§1.2质点的位移、速度和加速度一.位移位移矢量反映了物体运动中位置(距离与方位)的变化。讨论(1)位移是矢量（有大小，有方向）位移不同于路程(2)位移与参照系位置的变化无关(3)与Δr的区别OPP’OO分清\n二.速度(描述物体运动状态的物理量)1.平均速度O2.瞬时速度ABB'讨论(1)速度的矢量性、瞬时性和相对性。(2)注意速度与速率的区别\n三.加速度1.平均加速度2.瞬时加速度讨论(1)加速度反映速度的变化（大小和方向）情况。ABO(2)加速度的方向总是指向轨迹曲线凹的一面。\n§1.3用直角坐标表示位移、速度和加速度一.位移xyzO时刻t，质点位于P，位矢为时刻t+t，质点位于Q，位矢为时间t内质点的位移为建如图所示坐标，则\n二.速度1.平均速度2.瞬时速度速度的大小为速度的方向用方向余弦表示为\n三.加速度大小为方向用方向余弦表示为\n四.运动学的两类主要问题1.第一类问题已知运动学方程，求2.第二类问题已知加速度和初始条件，求对t微分对t微分对t积分对t积分\n1.第一类问题已知运动学方程，求(1)t=1s到t=2s质点的位移(3)轨迹方程(2)t=2s时已知一质点运动方程求例解(1)(2)(3)当t=2s时由运动方程得轨迹方程为\n解已知求和运动方程代入初始条件代入初始条件2.第二类问题已知加速度和初始条件，求例,t=0时，由已知有\n§1.4用自然坐标表示平面曲线运动中的速度和加速度一、速度—速度矢量在切线上的投影，是代数量—运动轨迹切线方向的单位矢量说明t0时，沿切线方向，且\n反映速度方向变化快慢二、加速度ABOPQ1.匀速圆周运动的大小的方向沿(t0时)方向R速度方向法向加速度速度矢量变化的快慢速度大小加速度反映ABO讨论OABOPQ\nABO2.变速圆周运动第二项：切向加速度第一项：反映速度方向变化的快慢P反映速度大小的变化反映速度方向的变化，指向圆心.法向加速度反映速度大小变化的快慢大小方向t0时，0，则沿切线方向\n3.变速曲线运动曲率圆\n一汽车在半径R=200m的圆弧形公路上行驶，其运动学方程为s=20t-0.2t2(SI).速度例汽车在t=1s时的速度和加速度大小。求解加速度\n将一根光滑的钢丝弯成一个竖直平面内的曲线，质点可沿钢丝向下滑动。已知质点运动的切向加速度为，g为重力加速度，为切向与水平方向的夹角.y0处质点的速度为v0由题意可知例质点在钢丝上各处的运动速度.求解\n已知质点运动方程为求之间的路程。例解速度速率路程\n已知质点的运动方程为在自然坐标系中任意时刻的速度解例求\n§1.5圆周运动的角量表示角量与线量的关系逆时针方向为正一.角位置与角位移质点作圆周运动的角速度为描述质点转动快慢和方向的物理量角位置（运动学方程)当为质点圆周运动的角位移二.角速度\n三.角加速度角加速度角速度对时间的一阶导数角加速度的方向与四.角量与线量的关系的方向相同1.位移与角位移的矢量关系式\n2.速度与角速度的矢量关系式大小方向(由右手法则确定)(标量式)3.加速度与角加速度的矢量关系式第一项为切向加速度第二项为法向加速度\n(2)与an成45o角，即(2)当=?时，质点的加速度与半径成45o角？(1)当t=2s时，质点运动的一质点作半径为0.1m的圆周运动，已知运动学方程为(1)求解例的大小则分析(1)(2)与成45o角，即\nAA`B`§1.6不同参考系中的速度和加速度变换定理简介同除以t若a车对地=0，即两系作匀速直线运动，则测得同一物体的加速度相等\n升降机以加速度1.22m/s2上升，有一螺母自升降机的天花板松落，天花板与升降机的底板相距2.74m。ha以升降机为参考系例解螺母自天花板落到底板所需的时间.求分析相对升降机，螺母作初速为0的落体运动，运动距离2.74m机对地匀加速运动\n一个带篷子的卡车，篷高为h=2m，当它停在路边时，雨滴可落入车内达d=1m，而当它以15km/h的速率运动时，雨滴恰好不能落入车中。求雨滴的速度矢量。根据速度变换关系例解分析相对车参照系，雨滴作落体运动矢量关系如图所示\n船逆流而上，遇一树时，箱子掉落水中顺水漂流，半小时后发觉，返回追赶，在树后5公里处赶上箱子。水流速度例解求地面参考系所以，船离开箱子、回追箱子所需时间相同。水流速度=5公里/小时5km水流参考系5km船速恒定，并且船离开箱子、回追箱子经过路程相同。\n一质点在水平面内以顺时针方向沿半径为2m的圆形轨道运动。此质点的角速度与运动时间的平方成正比，即ω=4t2。t=0.5s时质点(1)路程(2)加速度解例求路程(2)(1)角位移分析路程s=r，先求出角位移与切向夹角\n主要内容位矢速度加速度\n运动学的两类主要问题1.第一类问题已知运动学方程，求2.第二类问题已知加速度和初始条件，求对t微分对t微分对t积分对t积分\n角量线角关系