大学物理力学复习 22页

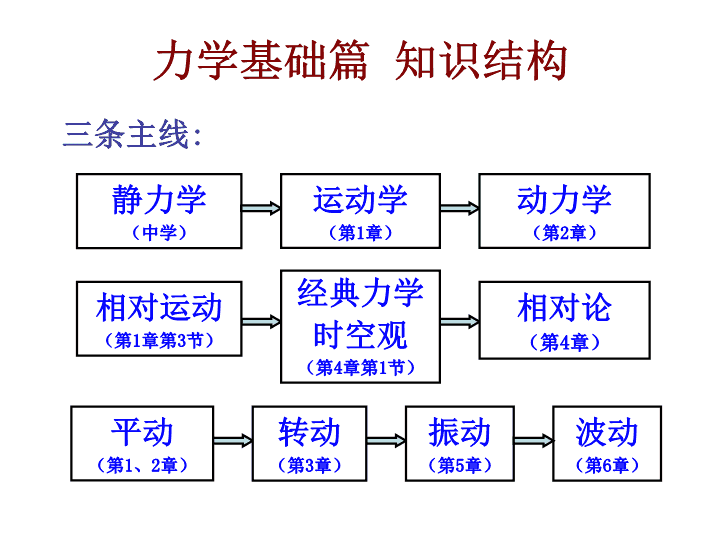
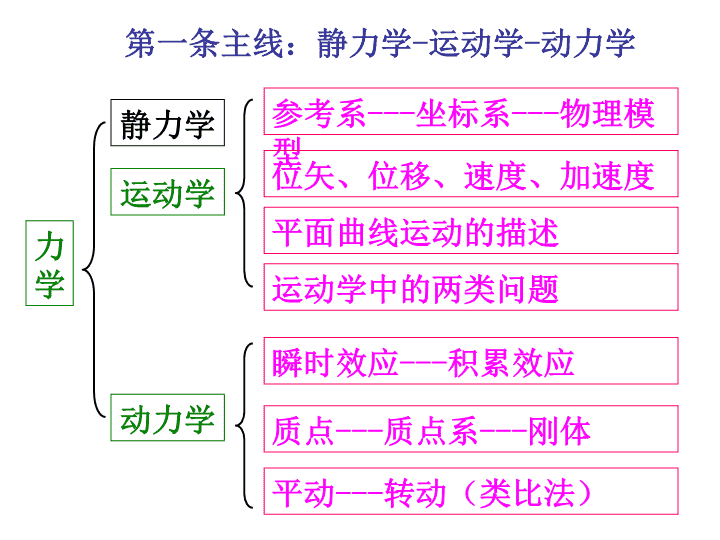
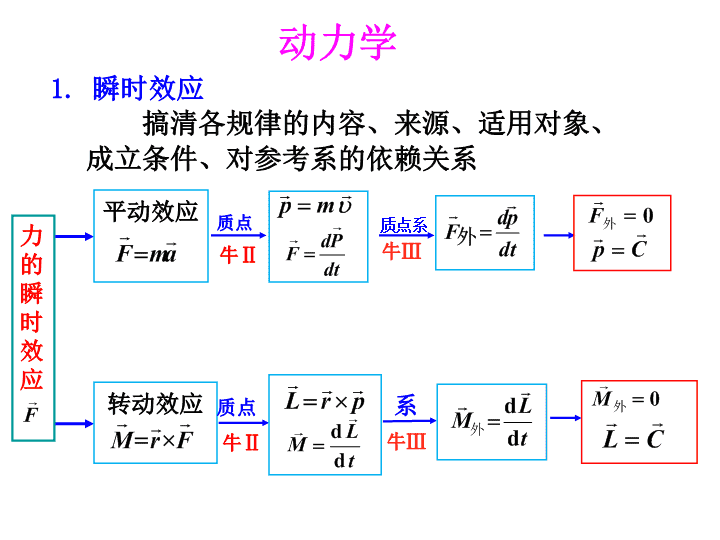
力学基础篇知识结构静力学（中学）三条主线:运动学（第1章）动力学（第2章）相对运动（第1章第3节）经典力学时空观（第4章第1节）相对论（第4章）平动（第1、2章）转动（第3章）波动（第6章）振动（第5章）\n力学静力学运动学动力学参考系---坐标系---物理模型位矢、位移、速度、加速度平面曲线运动的描述运动学中的两类问题平动---转动（类比法）质点---质点系---刚体瞬时效应---积累效应第一条主线：静力学-运动学-动力学\n1.瞬时效应搞清各规律的内容、来源、适用对象、成立条件、对参考系的依赖关系动力学力的瞬时效应平动效应质点系质点牛Ⅱ牛Ⅲ转动效应质点牛Ⅱ牛Ⅲ系\n2.积累效应力时间积累空间积累质点系质点牛Ⅱ牛Ⅲ牛Ⅲ质点牛Ⅱ一对力质点系质点系动力学\n平动转动力与冲量力矩与冲量矩质量与动量转动惯量与角动量平动动能转动动能力的功力矩的功势能平动与转动\n平动转动牛顿定律转动定律动量定理角动量定理动量守恒定律角动量守恒定律动能定理动能定理机械能守恒定律条件：（或只有保守力作功）平动与转动\n3.解题的基本方法与步骤(1)用牛顿定律解题(2)用功能、动量、角动量及守恒定律解题解题思路:(1)选系统(2)分析力(3)审条件(4)明过程(5)列方程\n例如图所示质量为M的物块A在离平板h的高度处自由下落，落在质量也是M的平板B上。已知轻质弹簧的倔强系数为k，物体与平板作完全非弹性碰撞，求碰撞后弹簧的最大压缩量。解：从物块A自由下落到弹簧压缩到最大限度可分为三个物理过程：(1)物块A作自由落体运动，到B时速度为v1;(2)物块A和平板B作完全非弹性碰撞，碰后速度为v2;(3)碰撞后弹簧继续被压缩到最大压缩量x2。\n以地球、弹簧、物块为一系统。第三个过程中只有重力，弹力作功，机械能守恒。取弹簧处于自然状态时，其上端点位置为坐标原点,重力势能、弹性势能零点，则第三个过程方程为对每个物理过程列出方程在A、B未碰撞前，B的重力跟所受弹力平衡，因此有kx1=mg解上述四式可得弹簧的最大压缩量x2\n例质量m1，半径为R的定滑轮（当作均质圆盘）上绕一轻绳，绳的一端固定在滑轮上，另一端挂一质量为m2的物体而下垂，如图所示。忽略轴处摩擦，求物体m2由静止下落h高度时的速度。解：根据机械能守恒定律\n二、经典力学时空观与变换（惯性系之间）伽利略变换一、相对运动（参考系之间）第二条主线：相对运动-经典力学时空观-相对论\n三、狭义相对论1.两个基本原理：光速不变原理与相对性原理。2.洛仑兹变换\n3、狭义相对论的时空观3.１同时的相对性３.3长度的相对性（动尺缩短）3.２时间间隔的相对性（时间膨胀）3.４因果关系信息传递速率小于光速，导致因果关系不会颠倒。S系同时同地同时异地异时同地异时异地S’系同时不同时不同时不能确定\n4、狭义相对论动力学4.１质速关系：4.２动量定义：4.３质能关系：4.４动量能量关系：\n解：①按地球上的钟例半人马座α星是离我们太阳系最近的恒星，地面观察者测得其距离是4.31016m，现宇宙飞船以=0.99c的速度由地面飞往α星①按地球的钟，飞到α星要多长时间？②按宇宙飞船上的钟，飞到α星要多长时间？②按飞船的钟\n第三条主线：平动-转动-振动-波动运动形式平动振动波动多普勒效应非自由振动与共振表达式图像与特征能量合成与叠加转动\n1、表达式振动波动弄清振幅、圆频率、位相的物理意义、关系与如何确定。明晰三种描述方法与关联、厘清振动的物理图像与特征。弄清波长、波速、周期的物理意义及它们之间的关系，注意波速与振速的区别。理解波动方程的物理意义。\n2、振动与波动图象振动图象描述的是一个质点的位移随时间变化的规律。波动图象描述的是给定时刻波线上所有各质点偏离各自平衡位置的位移随位置变化的规律。t\n3、能量（1）孤立的谐振动系统，其机械能守恒，动能和势能反相变化。（2）单位体积介质中的波动能量，机械能不守恒，动能与势能同步变化。总能量动能与势能振动守恒反相波动不守恒同步（3）注意波的平均能量密度、平均能流密度以及波的吸收。\n4、振动的合成与波的叠加同方向、同频率谐振动合成干涉相长干涉相消波的叠加与干涉相干条件干涉加强与减弱的条件同方向、不同频率谐振动合成注意：准谐振动，拍与拍频\n例一匀质细圆环质量为m，半径为R，挂在墙上的钉子上，试证明其作微小角度的摆动为简谐振动。转动惯量：1、对质心（圆心）水平轴的转动惯量为：由转动定律：2、依据平行轴定理，得对钉子处水平轴的转动惯量为：证：依据受力分析得所受力矩为：此为谐振动的动力学方程，故为简谐振动。证毕\n例如图所示，两列平面简谐相干横波，在两种不同的媒质中传播，在分界面上的P点相遇。频率v＝100Hz，振幅AA=AB=1.00×10-2m，SA的位相比SB的位相超前π/2。在媒质1中的波速ｕA=400m/s；SAP=rA=4.00m；在媒质2中的波速ｕB=500m/s；SBP=rB=3.75m。求P点的合振幅。rArBPSASB解：在P点引起的振动分别为：