大学物理-振动(1) 34页

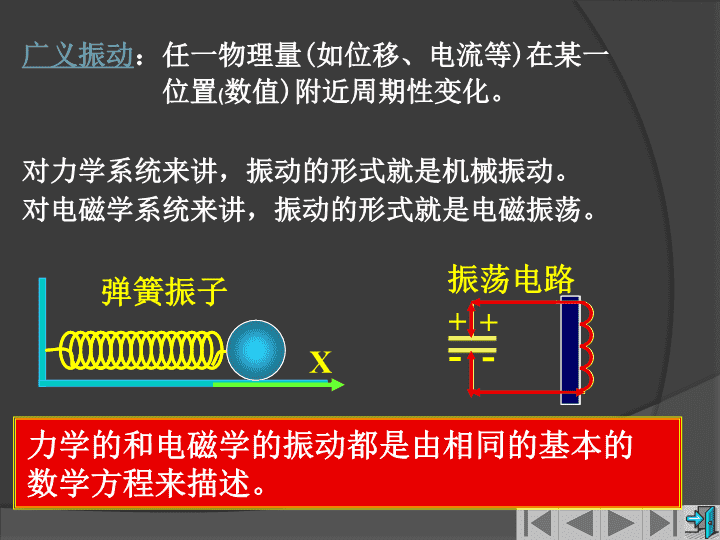
机械振动第九章\n教学重点：1、理解简谐振动的动力学特征及判定2、掌握振幅和初相位的确定及振动方程的建立方法3、旋转矢量法4、理解简谐振动的能量特征5、谐振动的合成\n广义振动：任一物理量(如位移、电流等)在某一位置(数值)附近周期性变化。对力学系统来讲，振动的形式就是机械振动。对电磁学系统来讲，振动的形式就是电磁振荡。++--弹簧振子振荡电路力学的和电磁学的振动都是由相同的基本的数学方程来描述。X\n复杂振动=简谐振动机械振动：物体在一定位置附近作来回往复的运动。振动是波动的基础，波动是振动的传播机械振动分类按振动规律分：简谐、非简谐、随机振动按产生振动原因分：自由、受迫、自激、参变振动按振动位移分：角振动、线振动。按系统参数特征分：线性、非线性振动其中简谐振动是最简单最基本的线性振动。\n重点：简谐振动的相关内容（判断、运动方程的建立)一、简谐振动的运动方程Xo§14--1简谐振动\n令：微分方程的解：谐振动的运动方程A的物理意义将在下面讨论\n在某一平衡位置附近作往复运动的物体，若它到平衡位置随时间变化的规律，具有和及的形式都称为简谐振动。如何判断物体或系统作简谐振动？\n单摆结论：单摆的小角度摆动振动是简谐振动。角频率,振动的周期分别为：当时摆球对C点的力矩\n复摆：绕不过质心的水平固定轴转动的刚体结论：复摆的小角度摆动振动是简谐振动。当时设：复摆对此固定轴的转动惯量为J\n例如图所示，一长为L的立方体木块浮于静水中，浸入水中部分的高度为b。今用手将木块压下去，放手让其开始运动。若忽略水对木块的黏性阻力，并且水面开阔，不因木块运动而使水面高度变化，证明木块作谐振动。bXmg解：以水面为原点建立坐标OX受力分析：列方程x\n故木块作谐振动（证毕）\n二、简谐振动物体的速度和加速度以上结果表明：(1)v，a与x的ω相同(2)(3)a与x方向相反，且成正比\n简谐振动的x,v,a三者之间的相位关系\n(2)角频率ω（Angularfrequency）：振动的快慢周期T：Period频率ν：(3)相位（Phase）：描述运动状态的量为初相位，InitialPhase对弹簧谐振子：三.描述简谐振动的物理量（A，ω，)振幅A（Amplitude）：离开平衡位置的最大距离（幅度、范围）。A2∝E\n4）振幅和初相的值是由初始条件决定的；A）初始条件：t=0时的初位移X0、初速度由：以t=0代入：\nXoA-A0oA-AX\n（2）一谐振动状态决定其振幅A、频率（或T或）初相。这三者称为振动三要素。理解注意：（1）周期、圆频率都是决定系统本身的物理量，称为固有周期、固有频率。3）在比较同频率的谐振动时，往往用到相位差的概念。振动“2”超前“1”振动“2”落后“1”振动“1”和振动“2”同相；规定：\n本节重点之一就是如何建立振动的运动方程，所涉及问题是如何确定振幅、初相、周期或圆频率。例：如图为物体作简谐振动时的x—t曲线，已知振幅为0.1m,周期0.5s。求初相位和简谐振动的运动方程。解：分析，从图可知t=0时：设振动方程为t\n以t=0代入：由所以由题意知所以振动方程为设振动方程为\n例：一弹簧振子，重物的质量为m，弹簧的劲度系数为k，该振子作振幅为A的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为：［B］\n例：求如图所示三种情况下振动系统的圆频率XOMm（a）m（b）m（c）\n解：图（a）（b）的情况下，和弹簧的伸长量和压缩量均相同，设为，而各产生的弹性力分别为，在重力作用下，其新的平衡位置移到M点设在平衡位置附近，有一微小位移x，则此时物体m受力为重力和弹性力的合力\n令其中为新的M平衡位置的位移则令则由（a）、（b）可见，振动系统除受弹性力之外还受重力的作用时，并不改变系统的振动规律，只会改变振动的平衡位置，系统（物体）仍作简谐振动。\n由图（c）：则有（1）（2）由（1）、（2）可得：m（c）\n为系统伸长单位长度时产生的弹性力的大小，即系统的等值倔强（劲度）系数K即讨论：1）弹簧的串联、并联求等值倔强系数K的方法：串联：并联\n讨论：2）若将一个劲度系数为K的弹簧，均匀分成n份，试问每一段的劲度系数：提问：有一劲度系数为K的轻弹簧被截成三等份，取出其中的两根，将它们并联在一起，再在下面挂一质量为m的物体，则振动系统的频率为：\n例：如图所示，一质量为m的滑块，两边分别与劲度系数为k1和k2的轻弹簧联接，两弹簧的另外两端分别固定在墙上．滑块m可在光滑的水平面上滑动，0点为系统平衡位置．将滑块m向右移动到x0，自静止释放，并从释放时开始计时．取坐标如图所示，则其振动方程为：［A］\n优点：除形象化外，还便于振动的合成。设有一简谐振动作大小为A的以旋转的旋转矢量的值由在X轴上的投影表示。XtXY14--2谐振动的矢量图示法\n位移、速度、加速度在旋转矢量图中的关系AXY假设\n由旋转矢量的参考圆可计算谐振动的一些相关物理量，例如：相位差、时间差。例：一物体沿x轴作谐振动，振幅为0.24m,周期为2s。当时，。且向x轴正方向运动，试求（1）振动方程；（2）从且向x轴负方向运动这一状态，回到平衡位置所需时间。\nOXP解（1）首先作参考圆，确定旋转矢量的位置；其次求出初相当时且易求得振动方程为：\nOXAA（2）作矢量图初态末态设所经历时间所对应的角度或由\n例：一个质点作简谐振动，振幅为A，，在起始时刻质点的位移为，且向x轴的正方向运动，代表此简谐振动的旋转矢量图为［B］\n例：一简谐振动曲线如图所示．则振动周期是(A)2.62s．(B)2.40s．(C)2.20s．(D)2.00s．［B］