大学物理-刚体的转动 43页

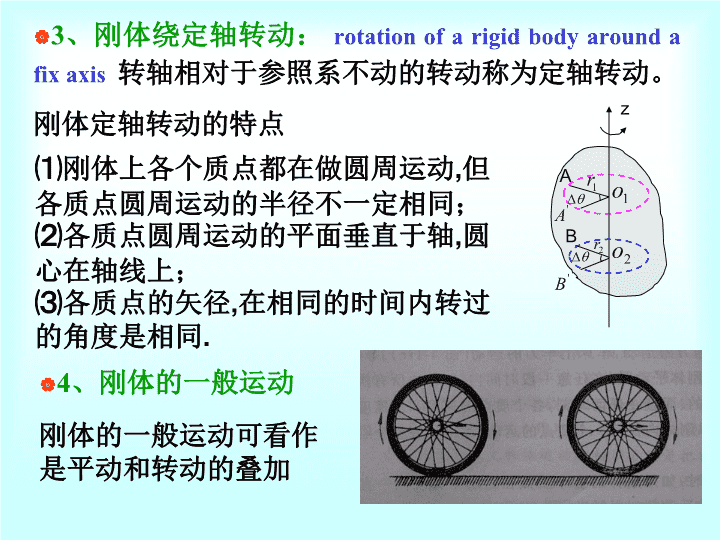
第三部分刚体的转动rotationofarigidbody\n1、刚体：rigidbody在力的作用下，大小和形状都保持不变的物体称为刚体。（组成物体的所有质点之间的距离始终保持不变）是一种理想模型。2、刚体的平动：translationofarigidbody刚体内所作的任何一条直线，始终保持和自身平行的运动。平动时，刚体上各点的运动轨迹都相同，因此，刚体上一点的运动可代表整个刚体的运动。(刚体平动的运动规律与质点的运动规律相同）§3.1刚体的平动、转动和定轴转动\n3、刚体绕定轴转动：rotationofarigidbodyaroundafixaxis转轴相对于参照系不动的转动称为定轴转动。刚体定轴转动的特点⑴刚体上各个质点都在做圆周运动,但各质点圆周运动的半径不一定相同；⑵各质点圆周运动的平面垂直于轴,圆心在轴线上；⑶各质点的矢径,在相同的时间内转过的角度是相同.ABz4、刚体的一般运动刚体的一般运动可看作是平动和转动的叠加\n5、角速度矢量：angularvelocityvectorOvP×,αrr定轴刚体参考方向θz刚体作定轴转动时，各质元的线速度、角加速度一般是不同的，但由于各质元的相对位置保持不变，所以描述各质元的角量，如角位移、角速度、角加速度都是一样的。因此描述刚体的整体运动时，用角量最为方便运动方程角速度角加速度角量与线量的关系\n例题：一飞轮以n=1500r/min的转速绕定轴作反时针转动。制动后，飞轮均匀减速，经时间t=50st停止转动。求：⑴角加速度和从开始制动到静止，飞轮转过的转数N；⑵制动开始后t=25s时飞轮的角速度；⑶设飞轮半径R=1m，求t=25s时飞轮边缘上一点的速度和加速度。Ov解：⑴转⑵⑶\n§3.2.1刚体的角动量转动动能转动惯量1、刚体的角动量angularmomentumofarigidbody质点的角动量（对一给定点而言）刚体绕轴的角动量即：把质点的角动量推广为刚体的角动量棒分成许多质点,第i个质点对O点的角动量的大小沿Z轴分量方向如图所示oz刚体对OZ轴的转动惯量\n2、刚体的转动动能rotationalkineticenergyofarigidbody刚体在转动时的动能，应该是组成刚体的各质点的动能之和。设刚体中第i个质点的质量为，速度为，则该质点的动能是整个刚体的动能式中正是刚体对转轴的转动惯量J刚体的转动动能\n3、刚体的转动惯量rotationalinertia(momentofinertia)质量连续分布时转动惯量与下列三个因素有关：⑴形状、大小相同的均匀刚体总质量越大，转动惯量越大。⑵总质量相同的刚体，质量分布离轴越远，转动惯量越大。⑶同一刚体，转轴不同，质量对轴的分布就不同，因而转动惯量不同。单位:体分布面分布线分布\n例题:三个质量为m的质点，A、B、C由三个长为L的轻杆相联结。求该质点系通过A点和O点，且垂直于三个质点所在平面的转轴的转动惯量。ABCO4、转动惯量的计算Calculationofmomentofinertia解：可见，同一刚体对不同转轴的转动惯量是不同的，只有指出刚体对某一转轴的转动惯量才有明确的意义。\n例题均匀杆质量m,长l，求杆对O轴和C轴的转动惯量。xdxxOlCl2l2解：平行移轴定理\n例题均匀圆环：例题均匀圆盘：rmiCR面密度\n半径为R质量为M的均匀圆盘联结一长为L质量为m的均匀直棒，写出刚体对O轴的转动惯量。（O轴垂直纸面）OmRML\n§3.2.2力矩刚体转动定律ZOdr1、力矩Momentofforce力F对O点的力矩力F对转轴OZ的力矩与转轴平行,不产生力矩在定轴转动中,几个外力同时作用在刚体上时,合外力矩为式中正负号根据右手螺旋法则规定\n刚体所受到的对于给定轴的总外力矩等于刚体对该轴的角动量的时间变化率比较转动惯量表示刚体在转动过程中表现出的惯性2、转动定律lawofrotation说明:*为合外力矩瞬时性：二者同时存在，同时消失同轴性：都是对同一确定轴而言\n转动定律的应用隔离物体，分析受力建立坐标，求力矩列出方程，求解应用：类似牛顿定律：\n刚体定轴转动定律的应用例题：一轻绳跨过一定滑轮，滑轮视为圆盘,绳的两端分别悬有质量为和的物体，，如图所示，设滑轮的质量为m，半径为r，所受的摩擦阻力矩为，绳与轮之间无相对滑动。试求物体的加速度和绳的张力。＜aa解：受力分析如图按牛顿运动定律和转动定律可列出下列方程\n从以上各式即可解得当不计滑轮质量及摩擦阻力即令\n例题：一半径为R，质量为m的均匀圆盘，放在粗糙的水平面上。设盘与桌面间的摩擦系数为，令圆盘最初以角绕通过中心且垂直盘面的轴旋转，问它将经过多长时间才停止转动？e解：取盘上一面积元根据转动定律设盘经时间t停止df\n质量为M的匀质圆盘可绕通过盘心，垂直于盘面的固定光滑轴转动，绕过盘的边缘挂有质量为m长为L的匀质柔软绳索，设绳与盘无相对滑动，求当盘两侧绳之差为s时，绳的加速度的大小。s解：选长为、两段绳和绕着绳的盘为研究对象\n§3.3定轴转动的中的功能关系1、力矩的功：workdonebytorqueozP表示作用在刚体上P点的外力，当物体绕轴有一角位移时，力做的元功为因为设刚体从转到，则力作的功为所有外力的功（力矩的功）式中为刚体所受到的总外力矩\n对于定轴转动刚体，所有内力的功总和在任何过程中均为零。（内力成对，大小相等方向相反，一对内力矩的代数和为零；∴内力矩的功总和为零。）力矩的功率2、转动动能定理rotationalkineticenergytheorem转动动能定理也与质点动力学中讲的动能定理相同，只是动能的表示形式不同而己。\n3、刚体的重力势能一个不太大的刚体的重力势能和它的全部质量集中在质心时所具有的势能一样。如图所示，已知滑轮转动惯量为J，半径为R，物体的质量为m，弹簧的劲度系数为k，系统从静止释放，释放时弹簧无伸长。求物体下滑x米时的速度。\/\/\/\/JRm光滑解:取物体m、滑轮、弹簧和地球为系统，系统只有重力和弹力做功，机械能守恒。\n一均匀细棒，可绕通过其端点并与棒垂直的水平轴转动。已知棒长为L，质量为m，开始时棒处于水平位置。令棒由水平位置自由下摆，求：⑴棒在任意位置时的角加速度和角速度；⑵棒摆至铅直位置时重力矩所做的功。OCCmg解：⑴棒在任意位置时的重力矩因为分离变量得\n积分所以这功即是细棒重力势能的减少⑴也可根据机械能守恒求角速度OCCmg⑵棒摆至铅直位置时重力矩所做的功重力势能零点\n一根细棒长为L，总质量为m，其质量分布与离o点的距离成正比，现将细棒放在粗糙的水平桌面上，棒可绕过其端点o的竖直轴转动，已知棒与桌面间的摩擦系数为，棒的初始角速度为，求：⑴棒对给定轴的转动惯量；⑵棒绕轴转动时受到的摩擦力矩；⑶棒从到静止所经过的时间；⑷棒转过一圈后的角速度。解：⑴设棒的线密度为\n⑵棒绕轴转动时受到的摩擦力矩f⑶棒从到静止所经过的时间⑷棒转过一圈后的角速度\n§3.4定轴转动刚体的角动量定理和角动量守恒定律1、定轴转动刚体的角动量定理angularmomentumtheoremofarotationalrigidbodyaroundafixaxis转动物体所受合外力矩的冲量矩等于在这段时间内转动物体角动量的增量------角动量定理。所以由转动定律\n2、定轴转动刚体的角动量守恒定律lawofconservationofangularmomentumofarotationalrigidbodyaroundafixaxis当物体所受合外力矩等于零时，物体的角动量保持不变。-------角动量守恒定律若则由角动量定理\n说明1、角动量定理和角动量守恒定律，不仅适用于宏观问题，也适用于原子、原子核等微观问题，因此角动量守定律是比牛顿定律更为基本的定律。2、角动量定理和角动量守恒定律只适用于惯性系。4、内力矩可以改变系统内部各组成部分的角动量，但不能改变系统的总角动量。3、角动量保持不变、恒矢量：①不变，也不变②变，也变，但保持不变。\n应用举例1、花样滑冰，芭蕾舞演员的表演：（绕通过重心的铅直轴高速旋转，由于外力（重力，支撑力）对轴的矩总为零，角动量守恒，通过改变自身的转动惯量，来改变角速度）。2、直升飞机尾部竖直的尾翼（产生一反向角动量，避免在水平面打转）3、跳水运动员，跳马（伸直，以初角速度起跳；卷缩，减小J，以增大角速度；伸直；入水时J增大了，减小角速度以保持竖直入水）\n一质量为M的均匀圆盘正以角速度旋转着，今有一质量为m，速度为v的铁钉，⑴从正上方⑵从正右方嵌入圆盘边缘，则圆盘的角速度分别变为多少？vvmmRMo解：角动量守恒⑴⑵\nA和B两飞轮绕同一中心线转动，它们的转动惯量分别为、，转动角速度分为、，。C为摩擦啮合器。求：⑴两轮啮合后的角速度；⑵啮合过程损失的能量；⑶两轮各自所受的冲量矩。ABC解：⑴系统角动量守恒⑵能量损失⑶冲量矩\n质量分别为、，半径分别为、的两均匀圆柱，可分别绕它们本身的轴转动，二轴平行。原来它们沿同一转向分别以、的角速度匀速转动，然后平移两轴使它们的边缘相接触，求最后在接触处无相对滑动时，每个圆柱的角速度。对上述问题有以下解法：在接触处无相对滑动时两圆柱系统角动量守恒由以上二式就可解出和，你对这种解法有何见解？其中⑴⑵\n解：原解⑵式是认为系统的角动量为二圆柱各自对各自的轴的角动量之和，这样的计算是错误的，因为系统的总角动量只能对某一个轴进行计算，此外，二圆柱在各自的轴处均受外力，因此不论对哪一个轴来说，这一系统的合外力矩均不为零，所以系统的角动量是不守恒的，正确的解法是用角动量定理，设二圆柱接触处的一对切向摩擦力为则有且有联立以上各式可解出正确的解。\n如图，一长为l,质量为M的杆可绕支点O转动，一质量为m，速率为v0的子弹，射入距支点为a的杆内，若杆的偏转角=300，求子弹的初速率v0例题解：此题分两个阶段，第一阶段，子弹射入杆中，摆获得角速度，尚未摆动，子弹和摆组成的系统所受外力对O点的力矩为零，系统角动量守恒：第二阶段，子弹在杆中，与摆一起摆动，以子弹、杆和地地球组成的系统除保守内力外，其余力不作功，于是系统机械能守恒：\n由（2）（3）（4）式求得：代入（1）式，得：其中：\n解：以人和转盘组成的系统为研究对象，设人相对于转盘的速度为vr，转盘相对于固定铅直轴的角速度为。当人走动时，系统所受外力对铅直轴之矩为零，故对轴角动量守恒：质量为M、半径为R的转盘，可绕铅直轴无摩擦地转动。转盘的初角速度为零。一个质量为m的人，在转盘上从静止开始沿半径为r的圆周相对转盘匀速走动，如图。求当人在转盘上走一周回到盘上的原位置时，转盘相对于地面转过了多少角度。例题\n所以设在t内，盘相对于地面转过的角度为其中为人相对于盘转过的角度，人走一周，则因此盘相对于地面转过的角度为：\nAB一轻绳绕过一半径为Ｒ，质量为m/4的滑轮。质量为m的人抓住绳的Ａ端，而绳的Ｂ端系了一个质量为m/2的重物。求人相对于绳匀速上爬时，重物上升的加速度。选人、滑轮与重物为系统，所受的外力矩为解：（方法一）设u为人相对绳的匀速度，v为重物上升的速度。则系统对轴的角动量为\n根据角动量定理既因故有（方法二）aa滑轮物人解得\n质点的直线运动(刚体的平动)刚体的定轴转动速度角速度加速度角加速度匀速直线运动匀角速转动匀变速直线运动匀变速转动现将平动和转动的一些重要公式列表对照\n力F,质量m牛顿第二定律F=ma力矩M，转动惯量J转动定律动量mv,冲量Ft（常量）动量定理角动量J,冲量矩Mt(常力矩)角动量定理动量守恒定律角动量守恒定律平动动能常力的功动能定理转动动能常力矩的功动能定理\n第三部分结束