大学物理--静力学 39页

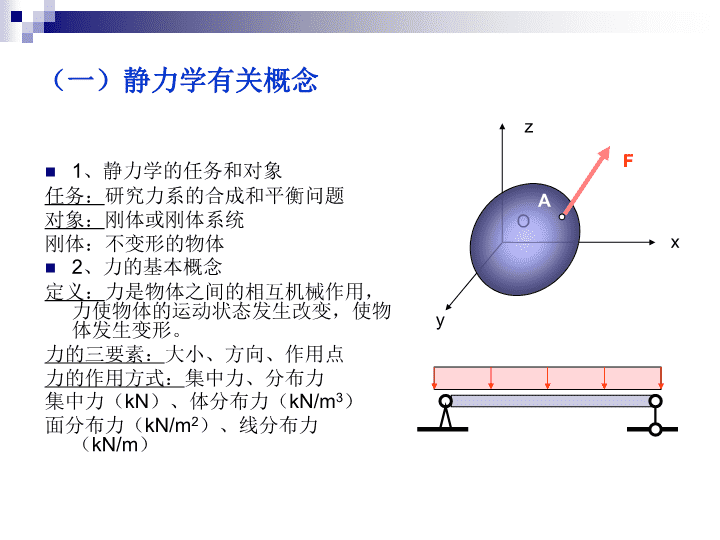
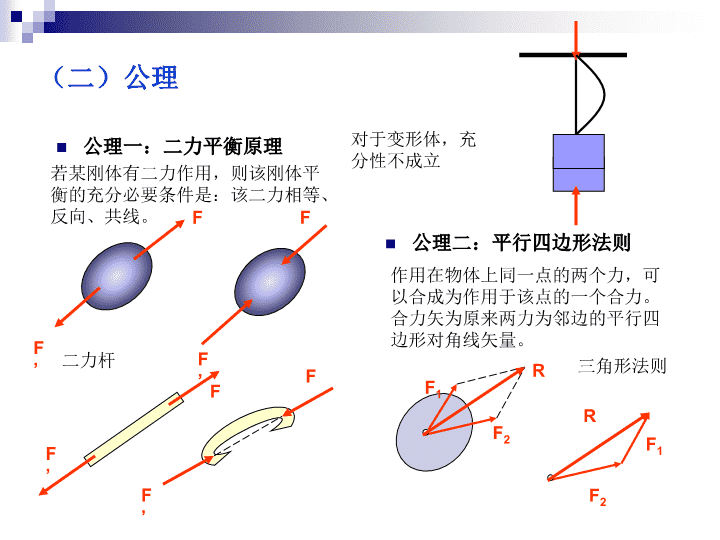
《静力学》讲义（1）静力学有关概念与公理（一）静力学有关概念（二）公理（三）约束（四）受力分析\n1、静力学的任务和对象任务：研究力系的合成和平衡问题对象：刚体或刚体系统刚体：不变形的物体2、力的基本概念定义：力是物体之间的相互机械作用，力使物体的运动状态发生改变，使物体发生变形。力的三要素：大小、方向、作用点力的作用方式：集中力、分布力集中力（kN）、体分布力（kN/m3）面分布力（kN/m2）、线分布力（kN/m）OxyzFA（一）静力学有关概念\n公理一：二力平衡原理若某刚体有二力作用，则该刚体平衡的充分必要条件是：该二力相等、反向、共线。F’FF’F二力杆F’FF’F对于变形体，充分性不成立公理二：平行四边形法则作用在物体上同一点的两个力，可以合成为作用于该点的一个合力。合力矢为原来两力为邻边的平行四边形对角线矢量。F2F1RF2F1R三角形法则（二）公理\n公理三：加减平衡力系原理（二）公理在作用于刚体上的任何一个力系中，加上或减去任意一个平衡力系，并不改变原力系对刚体的作用推论1：力的可传性作用于刚体上的任意力，可以沿该力作用线移动，而不改变该力对刚体的作用。FFF’’F’F’’推论2：三力平衡汇交定理若作用于刚体上的三力处在同一平面内，且相互平衡，则该三力必然汇交。F3F1F2R23注意该定理仅具有必要性，而不具有充分性。且仅适合于平面力系。\n（二）公理公理四：作用与反作用定律两个物体间的相互作用的力，即作用力和反作用力，总是等值、反向、共线。AF’FAA注意：1、力总是成对出现的；2、作用力与反作用力分别作用在两个不同的物体上，与二力平衡原理是完全不同的；小结：1、公理一和公理三仅适合于刚体，公理一是力系平衡的基本原理；2、公理二和公理四适合于刚体和变形体，适合于静力和动力问题。公理二是力系合成的基本原理\n（三）约束主动力和被动力主动力：一般指荷载被动力：一般指约束反力约束：与研究对象相连的周围物体，对研究对象的运动趋势构成限制。约束的类型1、光滑接触面：约束反力沿接触点外法线指向作用物体AητANAN’AAτηAτηNAN’A\n（三）约束2、柔体约束:约束反力沿柔体轴线背离作用物体ABABT’TT2’T1T1’T23、铰链:约束反力的作用点在铰心，方相待定。Ry’RxRyRx’4、固定铰支座:铰链的一种特殊情况，其中一端与地面相连。RyRx\n（三）约束5、可动铰支座：约束反力与地面垂直R6、链杆：约束反力沿链杆轴线方向，可拉可压ABABS’S固定铰支座可动铰支座链杆是一种最基本的约束单元。\n（四）受力分析受力分析的目的研究对象：可能是一个物体或由多个物体组成研究对象上受哪些力哪些力已知，哪些力未知（包括大小和方向）作受力图的步骤选择研究对象，去脱离体；画主动力；画被动力，即约束反力示例：碾子WFθαABWFθαABNANB\n（四）受力分析示例：斜梁αqAB受力分析1ABqYARBXA受力分析2qllBRBRA受力分析的两个层次按约束性质按力的简化和平衡要求\n（四）受力分析物体系：由多个物体通过某种联系组成的物体系统外力：施力者来自于物体系以外物体内力：物体系内物体之间的相互作用力示例：三铰架llCABq受力分析1整体分析CABqYBXAYAXBY’CXCYCX’C局部分析CAXAYACBYBXB\n（四）受力分析示例：三铰架（续）受力分析2：局部分析R’CCBRBRCCARAql示例：简易起重装置ABCDEWT拆分方案1WTYcXcWWRcBDEACR’cRARB\n（四）受力分析示例：简易起重装置（续）拆分方案2BECR’c1SEDRBACDWTSDERc1XAYA注意：选定研究对象一定要画脱离体图根据求解方法确定进行受力分析的层次主动力的作用方式不要随意改变、作用点不要轻易移动，尽量原汁原味确定约束反力方向时，一定要有依据\n《静力学》讲义（2）平面汇交力系（一）几何法（二）解析法\n（一）几何法力系的合成OF1F3F2OF1F3F2R12ROF1F2RF3作力多边形，各力首尾相连，合力为封闭边。各力顺序不同，力多边形的形状不同，但合力相同。F1F2RF3力系的平衡平面汇交力系平衡的几何条件是：力多边形自行封闭OF1F3F2\n示例：碾子。W=5kN,F=2kNWF300300ABWFABNANB300300W-NBFNA3003001、受力分析2、作力多边形W-NBFNA300300F要多大才能拉动碾子此时有NB=0WFNA300300（一）几何法\n（一）几何法示例：三铰架。q=2kN/m,l=2mllCABql1、受力分析R’CCBRBRCCARA4kN2、作力多边形4kN450θθRCRADE作图计算tgθ=AE/DE=0.5/1.5θ=18.430\n（二）解析法力的分解和投影FyxOFyFxYX注意：分力和投影的意义是不同的FyxOFyFxYXθ力系的合成\n（二）解析法力系的平衡平面汇交力系的平衡条件是2个独立的平衡方程，可以解出2个未知力示例：斜梁3002kN/mAB2m1、受力分析4kNBRBRAADC300θxy4kNRAθRB3002、平衡求解\n（二）解析法示例：简易起重装置。求支座反力ABCDEWT6001、受力分析WWRCBDEACRARBFG450300θ2、平衡求解\n《静力学》讲义（3）力对点之矩、平面力偶系（一）力对点之矩（二）平面力偶系（三）力的平移\n（一）力对点之矩FOh力F对O点之矩为其几何意义是BA力对点之矩是力对物体转动效应的度量，它取决于两个方面力的大小和指向；矩心的位置。合力矩定理：平面汇交力系的合力对某点之矩等于各力对该点之矩的代数和。FyOFyFxYXxy单位：kNm,Nm\n（一）力对点之矩示例：大坝。求各力对B点之矩。9m3m2.7mP1P2G1G23m0.6mP1=400kN,P2=80kNG1=450kN,G2=200kNBA0.6md\n（二）平面力偶系F’F力偶：等值、反向、平行的一对力d力偶矩：单位：kNm,Nm组成力偶的两个力对力偶作用面内的任一点取矩恒等于力偶矩本身。cO在同一平面内的两个力偶等效的必要与充分条件是两力偶之矩相等。示例：求力系对A、B点的力矩2kN/m5kN3kNm1m2m1mBA1、力偶、力偶矩\n（二）平面力偶系2、平面力偶系的合成与平衡平面力偶系可以合成为一个合力偶，该合力偶的力偶矩等于各力偶矩的代数和。平面力偶系平衡的充分必要条件是，各力偶矩的代数和为零。300A2m示例：斜梁。求支座反力3kNmRARB力对点之矩和力偶矩在平面力系中都是代数量力对点之矩随点的位置变化而变化力偶矩对物体任一点的转动效应都是相同的\n（三）力的平移FAFAF”BAF’BM=Fdd平移定理:力在刚体上可以向平面内任意点平移，但必须附加一力偶，该力偶矩等于原力对平移点取矩。FeFM\n《静力学》讲义（4）平面任意力系（一）力系的简化（二）力系的平衡（三）平面平行力系\n（一）力系的简化1、力系向一点的简化F’2F’1F1F2F3M1M2M3M0R’F’3简化结果：一个主矢和一个主矩主矩大小和转向则随简化中心位置而变化主矢大小和方向不随简化中心位置而变化\n（一）力系的简化2、简化结果的讨论主矢为零，主矩为零。平衡力系主矢为零，主矩不为零。平面力偶系主矢不为零，主矩为零。简化中心恰好是合力作用点主矢不为零，主矩不为零。一般情况4、合力矩定理M0R’R’R”dRRR则为力系的合力平面力系的合力对某点之矩等于该力系各力对该点的代数和\n（一）力系的简化示例：求力系的合力大小和作用线位置。Oxy5kN(-3,0)(3,-4)3kN3004kNmOxy5.94143.40R’MoR143.40\n（一）力系的简化示例：求力系的合力大小和作用点。q0hxqdxRxC示例：求力系的合力大小和作用点。2kN/m5kN3kNm1m2m1mBARxC\n（一）力系的简化3、固定端的约束反力MAXAYA\n（二）力系的平衡1、平衡方程可以解出三个未知力示例：刚架aaaaP=2qaqP=2qaqRAxRAyMAΣX=0,RAx-qa=0ΣY=0,Ray-2qa=0ΣmA=0,MA+2qa×a-qa×3a/2=0MA=-qa2/2\n（二）力系的平衡示例：图示三角支架。求A、C处的支反力。CAB30cm30cm600Q1=12kNQ2=7kNABQ1=12kNQ2=7kNSXAYA300基本方法二力矩方程：去掉ΣY=0方程三力矩方程：再去掉ΣX=0方程\n（二）力系的平衡2、平衡方程的其它形式二力矩式∑X=0,R与y平行∑mA=0,R通过A点∑mB=0,R为零yxORAB三力矩式∑mA=0,R通过A点∑mB=0,R通过AB连线∑mC=0,R为零yxORABCR\n（二）力系的平衡示例：斜梁。求支座反力2kN/mAB2m3002kN/mBARBYAXACD300300\n（二）力系的平衡ABCDEWW600示例：简易起重装置。求支座反力YAXARBa解题步骤选取研究对象受力分析列平衡方程。恰当选择投影轴或矩心，尽量一个方程求解一个未知量校核\n（三）平面平行力系xOy可以解出二个未知力示例：外伸梁。求支座反力2kN/m4kN4m4m4mRARBΣmA=0,RB×8-2×4×2-6-4×12=0RB=8.75kNΣY=0,RA+RB-2×4-4=0RA=3.25kN6kNmBA\n（三）平面平行力系示例：吊车。PWQdabcBA求Q的取值范围RARB